悬链线形断面临界水深的直接计算公式
2016-03-22张守都扬州大学水利与能源动力工程学院江苏扬州5009江苏省洪泽湖水利工程管理处江苏洪泽00中国水利水电科学研究院水利研究所北京00048
陈 诚,龚 懿,夏 熙,胡 璟,张守都(. 扬州大学水利与能源动力工程学院,江苏 扬州 5009;. 江苏省洪泽湖水利工程管理处,江苏 洪泽 00;. 中国水利水电科学研究院水利研究所,北京 00048)
悬链线形过水断面的水力性能优于梯形和抛物线形等断面[1],且具有良好的结构性能,因而在渠道工程中得到较为广泛的应用。悬链线形断面临界水深的计算涉及众多的参数,其过程较为繁琐和复杂。由于其临界水深的无量纲方程为含反双曲余弦函数的高次方程,形式十分复杂,难以借助迭代理论推求能够满足高精度要求的简化计算公式。对于梯形[2-4]、圆形[5,6]、城门洞形[7-9]等断面临界水深的计算,国内外学者已进行了较多的研究,提出了不少直接计算公式,解决了一定的工程实际问题。目前,关于悬链线断面临界水深计算的研究还很不充分,直到2010年之前仍未见相关报道,目前也仅有两套直接计算公式[10,11]。徐军辉等[10]最先展开了有关悬链线断面临界水深计算的研究,提出基于不动点迭代理论的直接计算方法,但收敛速度较慢,且仅借助一元二次多项式计算迭代初值,精度无法满足工程实际的需要。运用优化拟合方法,滕凯和王荣[11]给出了一个近似计算公式,其形式较为简洁,最大相对误差绝对值为0.515%,精度仍不够高。冯雪和马子普[12]利用MATLAB语言编程来计算临界水深,需要借助计算机编程进行求解,不便于在实际工程中推广应用。
本文从悬链线形断面临界水深的无量纲关系式出发,提出新的拟合函数模型,对工程适用参数范围内的近2 000组数据进行逐次优化拟合,建立新的临界水深直接计算公式。该公式精度很高,在工程适用范围内的最大相对误差绝对值小于0.10%,平均相对误差绝对值小于0.021%,且具有简明直观、物理概念清晰明确等特点,可供工程设计人员用于高精度临界水深值的计算。
1 临界水深基本方程
如图1所示,悬链线形断面的方程为:
(1)
式中:a为断面形状参数(a>0),m;e为自然常数。
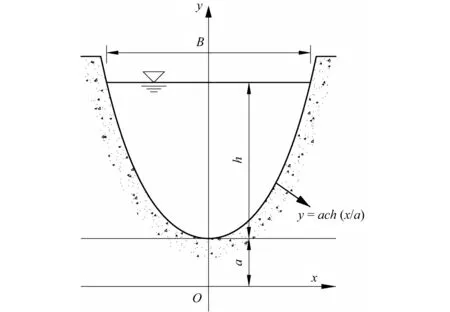
图1 悬链线形过水断面Fig.1 Catenary water transfer cross section
相应于临界流的过水断面的水力要素为:
(4)
(5)
式中:hk为临界水深,m;Ak为相应于临界水深时的过水断面面积,m2;Bk为相应于临界水深时的水面宽度,m;χk为相应于临界水深时的湿周,m。
根据水力学中的临界流理论,临界流的基本方程[13]为:
(6)
式中:α为流速分布不均匀系数,通常取1.0~1.1;Q为流量,m3/s;g为重力加速度,一般取9.81 m/s2。
可以推得悬链线形断面临界水深的基本方程:
(7)
为便于分析和计算,引入无量纲临界水深x和无量纲参数k:
(8)
(9)
为方便起见,将式(7)用反双曲余弦函数的形式表达。通过简单的数学变换,可推得关于悬链线形断面无量纲临界水深的基本方程:
(10)
令η=B0/a(B0为相应于正常水深时的水面宽度)。实际工程中,断面形状参数a通常不给定,而是根据具体情况先选定η值,再求出a。可根据式(11)计算断面形状参数a。
(11)
式中:Q为流量,m3/s;n为糙率系数;i为渠道底坡。
2 悬链线形断面临界水深的直接计算公式
实际工程设计中,可以根据已知条件求得无量纲参数k,但无法根据式(10)对无量纲临界水深x直接进行求解,本文旨在提出一套高精度的近似公式x=g(k) (最大相对误差绝对值小于0.10%),由k直接求解x,进而求得临界水深hk。无量纲临界水深x的取值范围取x∈[0.09,11.00][11],以此作为本文近似公式初选的工程适用范围。
运用MATLAB 8.5软件的Curve Fitting Toolbox,以0.01为步长对x∈[0.09,11.00]范围内的1 092个数据点进行曲线拟合,将各类函数模型的拟合效果进行反复比对,始终难以找到能够满足0.10%高精度要求的函数模型。但发现通过选取适当的参数,x=akb+clnk+d的函数曲线与式(10)的函数曲线能够在在大部分区间范围内高度吻合,只在x∈[0.09,1]区间内的拟合精度相对较低,故考虑采用分段函数的形式,对[0.09,1.1]、[1.1,11.0]两个区间内共计近2 000个数据点分别进行逐次优化拟合,最终得到一套高精度的直接计算公式:
(12)
3 精度分析与评价
3.1 现有的直接计算公式
目前仅有两套关于悬链线形断面临界水深的直接计算公式,分别如下所示:
(1)徐军辉等[10]迭代公式:
μ0=-0.000 3k2+0.184 4k+0.901 8
(13)
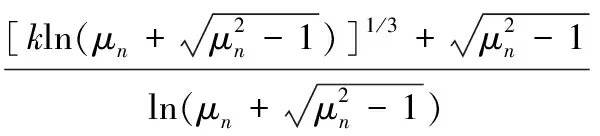
(14)
x=μ-1
(15)
(2)滕凯等[11]近似公式:
x=exp(71.048k0.003 6-70.899)
(16)
3.2 公式误差分析及评价
为验证式(12)的精确性,将本文公式与目前的两套计算公式进行精度对比,在工程适用参数范围内选取不同的xi(作为无量纲临界水深的精确值x*),根据式(10)算出与之相对应的ki,将ki作为已知条件分别代入本文公式、徐军辉等[10]公式(迭代4次)和滕凯等[11]公式计算无量纲临界水深x′,并由式(17)计算相对误差,计算结果见表1和图2。
(17)
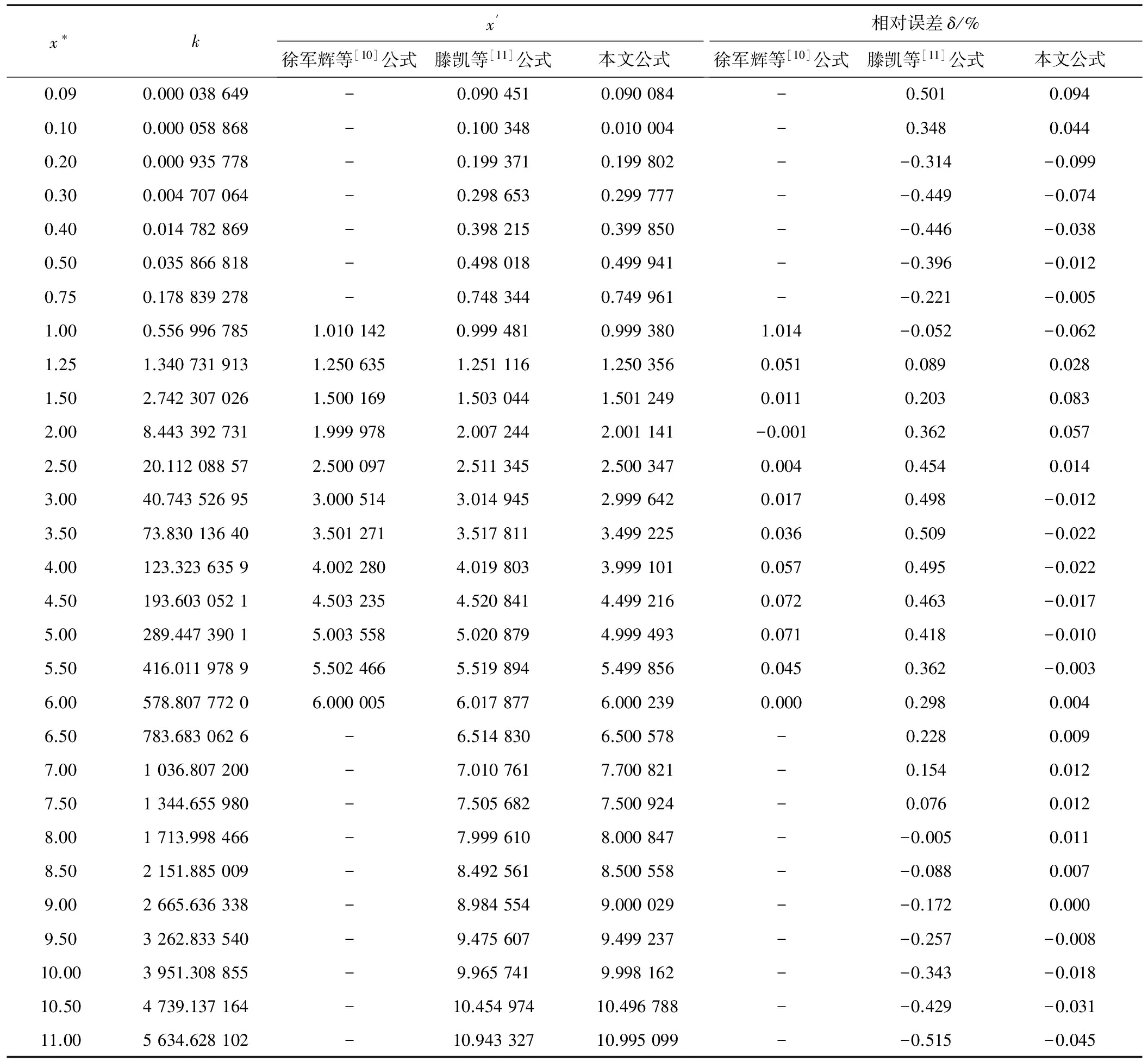
表1 工程适用范围内各类计算公式的相对误差Tab.1 Relative errors of various calculation formulae within practical range
注:“-”表示无法得到计算结果,公式不适用。
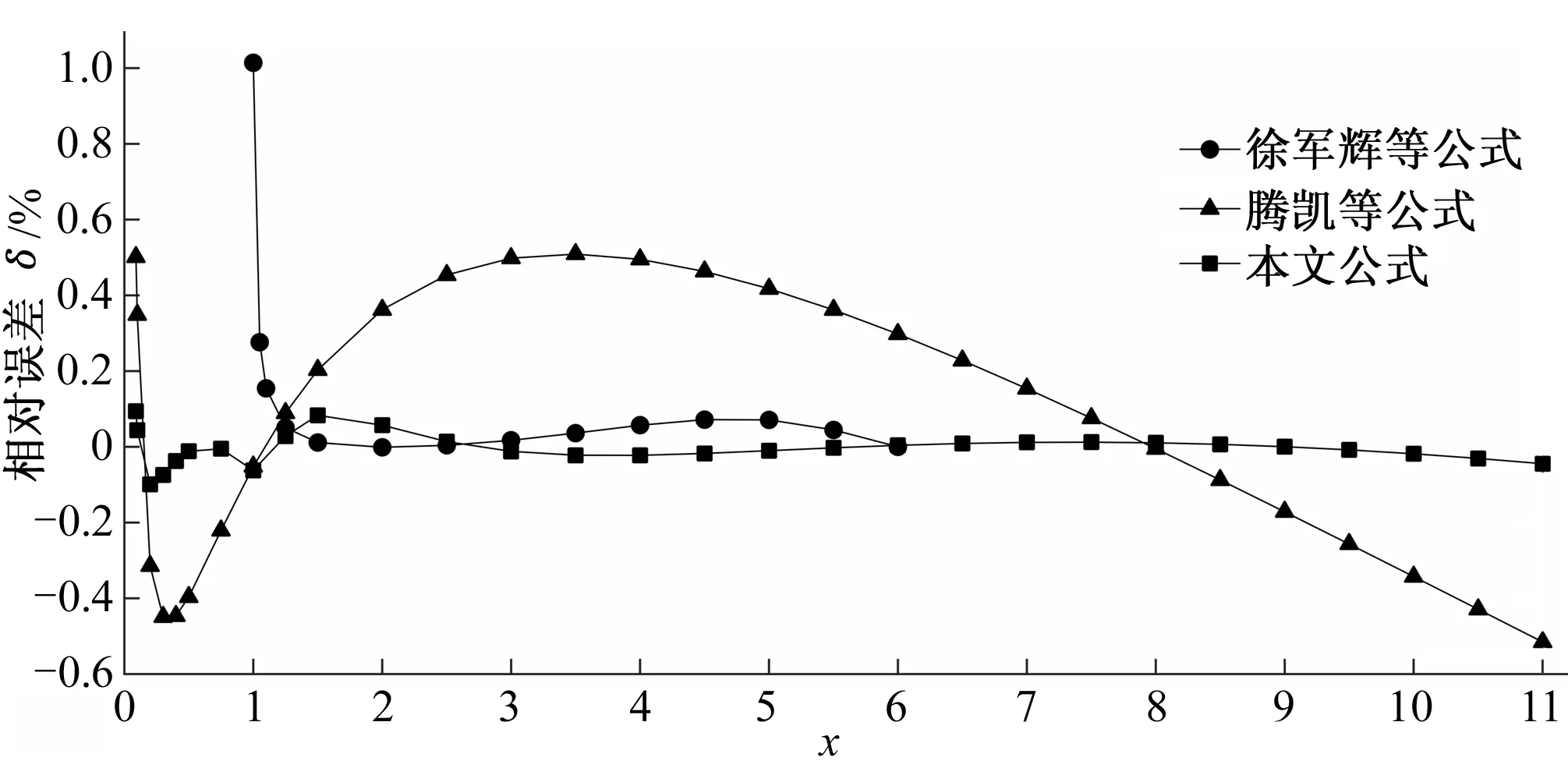
图2 各类计算公式的相对误差分布图Fig.2 Relative error diagram of various calculation formulae
从表1和图2可以看出,徐军辉等[10]迭代公式仅在x∈[0.989,6.095]时收敛,适用范围有限,且需通过反复迭代计算以提高精度,计算量较大。本文公式的最大相对误差绝对值仅为0.099%,小于滕凯等[11]公式的0.515%。分别计算本文公式与滕凯等[11]公式在[0.09,11.00]区间(以0.01为间隔)内的1 092个数据点的相对误差,取绝对值后求平均值,得本文公式的相对误差平均值仅为0.021%,小于滕凯等[11]公式的0.303%;对于1 092个点中97%以上的数据点,本文公式的相对误差绝对值小于滕凯等[11]公式。
本文提出的直接计算公式虽采用分段的形式,但在较宽的工程适用范围内(x∈[1.079 6,12.612 9],对应k∈[0.753 1,9 360.02]),近似公式x=0.964k0.276 9+0.030 43lnk+0.195 9均能满足相对误差绝对值小于0.1%的高精度要求,在形式上也仅比滕凯等[11]公式多了一个计算参数,计算较为简便,具有很大的工程实用价值。
4 应用实例
已知某输水渠道的过水断面为悬链线形,设计流量Q=10 m3/s,流速分布不均匀系数α=1.0,渠道底坡i=1/1 000,渠床糙率系数n=0.014,选用η=3.212 23,取重力加速度g=9.81 m/s2。试计算该渠道的临界水深hk。按如下步骤进行计算:
(1)将已知条件代入式(11)得断面形状参数a=1.171 719 587 m;
(2)由式(9)算得无量纲参数k=1.153 858 496>0.773;
(3)将k代入式(12)算得无量纲临界水深x=1.203 222 881;
(4)将x与a代入式(8)得临界水深hk=1.409 839 817 m。
通过计算机编程可求得本算例临界水深的精确值为1.409 782 932 m,本文公式计算结果的相对误差小于0.004 1%,绝对误差小于0.057 mm,精度完全满足实际工程的要求。
5 结 论
本文在充分分析临界水深无量纲方程数学特性的基础上,对其工程适用范围内的近2 000个数据点进行逐次优化拟合,建立新的拟合函数模型,提出悬链线断面临界水深的直接计算公式,在工程适用范围内的最大相对误差绝对值及平均相对误差绝对值分别小于0.10%和0.021%,远远小于现有的两套计算公式。本文公式具有很高的计算精度,且适用范围广、计算较为简便,克服了传统的试算法和图表法的不足,以及迭代法计算过程复杂的缺点,完全满足工程实际的需要,在悬链线断面渠道的工程设计中具有很大的应用价值。
□
致谢:感谢扬州大学水利与能源动力工程学院院长程吉林教授和副院长吉庆丰教授在论文写作过程中给予的悉心指导和帮助。
[1] 金兆森,钱爱云,程吉林.小型衬砌渠道优化设计研究综述[J].节水灌溉,1998,(3):22-25.
[2] Vatankhah A R.Explicit solutions for critical and normal depths in trapezoidal and parabolic open channels[J].Ain Shams Engineering Journal,2013,4(1):17-23.
[3] Vatankhah A R,Easa S M.Explicit solutions for critical and normal depths in channels with different shapes[J].Flow Measurement and Instrumentation,2011,22:43-49.
[4] 徐海嵩,把多铎,张国辉,等.梯形明渠临界水深直接计算公式研究[J].西北农林科技大学学报(自然科学版),2014,42(9):206-210,218.
[5] Vatankhah A R,Bijankhan M.Choke-free flow in circular and ovoidal channels[C]∥ Proceedings of the Institution of Civil Engineers,Water Management,2010,163(4):207-215.
[6] 李 蕊,王正中,王志刚.圆形断面临界水深新近似计算式[J].干旱地区农业研究,2013,31(4):54-56,103.
[7] 张宽地,王光谦,吕宏兴,等.明流条件下城门洞形隧洞临界水深的直接计算法[J].四川大学学报(工程科学版),2010,42(3):101-106.
[8] Vatankhah A R.Direct solutions for normal and critical depths in standard city-gate sections[J].Flow Measurement and Instrumentation,2012,28:16-21.
[9] Liu J L,Wang Z Z,Leng C J,et al.Explicit equations for critical depth in open channels with complex compound cross sections[J].Flow Measurement and Instrumentation,2012,24:13-18.
[10] 徐军辉,金中武,卢金友,等.悬链线形渠道临界水深的计算方法[J].人民长江,2012,43(11):71-73.
[11] 滕 凯,王 荣.悬链线形断面渠道临界水深的简化计算[J].水利与建筑工程学报,2013,11(2):95-97,102.
[12] 冯 雪,马子普.悬链线形渠道正常水深与临界水深的计算方法[J].水电能源科学,2012,30(11):88-90.
[13] 清华大学水力学教研组.水力学(修订版)[M].北京:高等教育出版社,1980.
