四元联系数在区域水资源承载能力评价中的应用

2016-03-22山东水利职业学院山东日照276826

节水灌溉 2016年11期

李睿冉(山东水利职业学院，山东日照 276826)

随着我国社会经济发展、城镇人口的增长及生活水平的不断提高，水资源越来越短缺，用水量及污水排放量却日益增加，这成为制约我国社会经济发展的重要因素。水资源承载能力分析就是探讨水资源、人口以及区域经济三者的关系[1]，合理利用水资源，使得水资源与社会经济协调发展，对国家或者区域的综合发展来说，水资源承载能力评级至关重要[2]。自上世纪以来，我国对水资源承载能力的研究主要有模糊综合评价法[3]、投影寻踪法[4]、最优化方法[5]。模糊综合评价法以全面考虑风险指标的影响，多因素、多层次实现风险目标的评价。投影寻踪法是通过寻找能最大程度反映数据特征和最能充分挖掘数据信息的最优投影方向向量，来进行对不同区域水资源承载能力进行评价。最优化方法有两种思路，一种是以达到承载最大人口数量为目标，一种是以同时使多个目标达到最优的方案。在目前的水资源承载能力评价中，大多局限于静态评价，不能完全呈现出区域特点及发展目标。集对分析是一种不确定性分析问题的方法[6]，能够将水资源承载能力区域特点及社会经济发展的确定性和不确定性反映出来。而在集对分析基础上的四元联系数可以将不确定性因素分析较为准确地表达出来，可定量评判出日照市水资源承载能力级别。集对分析目前各类评价中有广泛的应用，常用于水资源可持续利用、生态环境、水资源与社会经济协调发展等评价中。本文将改进的集对分析方法应用于水资源承载能力评价中，为水资源承载能力评价提供了一种新的思路。

1 基于四元联系数的区域水资源承载能力评价方法

1.1 四元联系数原理

四元联系数是对集对分析思想的一种延伸, 具体体现在它将三元联系数中不同的部分进行细化，分为偏同异和偏反异，看似微小的区分,但对于集对分析来说,使得其更加完整有效,能更加准确地分析其不确定信息[7]。其表达式可写为[6]：

μ=a+bi+cj+dk

(1)

式中：a为同一度；b为偏同差异度；c为偏反差异度；d为对立度；它们均在[0,1]之间取值，且满足四者之和为1 ；i、j为差异不确定系数，i∈[0,1]，j∈[-1,0]；k为对立系数，k=-1；有时i，j，k不取值，只作为一个符号。

假设评价指标有n个，现进行集对(Ap,B)组合，集合Ap=[vp,1,vp,2,…,vp,l,…,vp,n]，Ap代表第P标准等级的若干指标，B=[x1,x2,…,xl,…,xn]，B代表n个评价对象。假设B内的指标均为效益型指标，比较(Ap,B)中的各对应项vp,l和xl，根据文献[8]中的公式可得到指标xl相对于1级指标的四元联系数(其他级别可用类似方法得到)。

(1)若xl∈[v1,l，+∞]，则：

μ=1+0i+0j+0k

(2)

(2)若xl∈[v2,l，v1,l]，则：

(3)

(3)若xl∈[v3,l，v2,l]，则：

(4)

(4)若xl∈[0，v3,l]，则：

μ=0+0i+0j+1k

(5)

式中：v1,l，v2,l，v3,l分别为评价标准1级、2级、3级的门限值；xl为评价的各指标值。

1.2 区域水资源承载能力评价

现将四元联系数应用于水资源承载能力评价，将水资源承载能力分为3级[9]，分别对应于“弱”、“中”、“强”3个级别。“弱”代表当地水资源承载能力达到饱和，无进一步开发的潜力，水资源与当地经济已无法协调发展；“中”代表仅对当地水资源进行了部分开发，仍有进一步开发的潜力，水资源能够在一定程度上满足当地经济发展需求；“强”代表当地水资源状况很好，仍有很大的开发潜力，水资源与当地经济已无法协调发展；现进行评价对象空间设定，设A={水资源承载能力评价指标}，属性空间B={水资源承载能力评价等级}，用m代表一级子系统[10]，它在[1,4]之间取值，水资源承载能力的四元联系度分别用一级、二级及总指标来表示 (A-B)，进一步分析水资源承载能力评价系统中分级标准与评价指标之间的量化关系。具体步骤[8]如下。

(1)a，b，c，d取值的确定。若指标值处于评价级别中，则a=1，b=c=d=0；若指标值处于两个级别数值之中时，则d=0，如果指标值离现状评价等级越近，则a越大，反之c越大；若指标值在评价等级的上一个或下一个等级中，则a=0，距本评价等级远时d大，近时b越大；若指标值处于评级等级的两个级别以下或以上时，则d=1，a、b、c皆为0[8]。

评价等级的指标在转换为效益型指标后进行分析计算，根据公式(2)～(5)计算出水资源承载能力相对于1级的联系度，得出相应参数值。

(2)区域水资源承载能力的一级子系统评价：

μm=rm1+rm2i+rm3j+rm4k

(7)

式中：q为相应子系统属性指标；pl一级下的二级指标数；wmq为二级子系统权重；rm1，rm2，rm3，rm4为指标系数。

(3)区域水资源承载能力总指标综合评价：

μ=r1+r2i+r3j+r4k

(8)

(9)

式中：wm为一级系统综合权重；r1，r2，r3，r4代表相应联系度参数。

(4)2级和3级标准联系度参数用以上方法可得，水资源承载能力大小由联系度数值确定。

2 模糊四元联系度在日照水资源承载能力中的应用

2.1 指标体系的建立

评价水资源承载能力需要对水资源可持续利用进行分析，区域水资源承载能力评价指标体系的建立是进行水资源承载能力评级的前提，建立一套体现水资源开发利用状况、社会经济状况及生态环境的评价体系为该区域发展提供决策支持，使区域的发展沿着正确的轨道进行。该指标体系建立过程中，各指标要遵循区域性、规范性、科学性和实用性原则区[11]，建立一组相互联系又相互独立的能进行量化的区域水资源承载能力评价因子，组成一个评价指标体系，该指标体系能够反映区域水资源承载能力[9]。然后，通过对评价指标体系将指标标准值与实际值比较，从而来监测、评价水资源承载能力所达到的水平。马峰根据河北石家庄现状，选择人均生活用水量、节水灌溉率等18项指标建立水资源承载力评价指标体系。陈南祥根据河南禹州市水资源及社会经济现状，选取了人均水资源量等8项指标作为区域水资源承载能力评价指标。本文根据日照市水资源现状，将其水资源承载能力系统从7个指标进行描述，7个指标对应水资源自然支持力、社会经济技术水平、社会生活水平、生态水平4个系统，针对现状给出一个标准值[5]，区域水资源承载能力评价指标体系分级表(见表1)，表1中还给出了日照市水资源承载能力现状值。

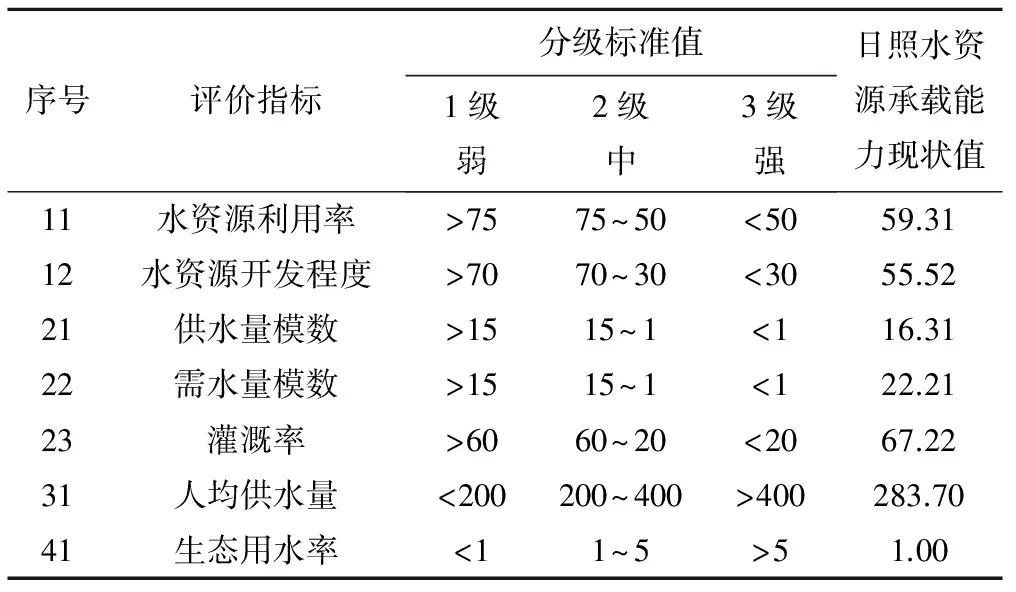
表1 区域水资源承载能力指标体系及等级标准

2.2 评价结果

根据区域水资源承载能力4个方面的具体情况，4个方面各占权重25%。由公式(2)～(6) 区域水资源承载能力评价一级指标的四元联系数见表2。

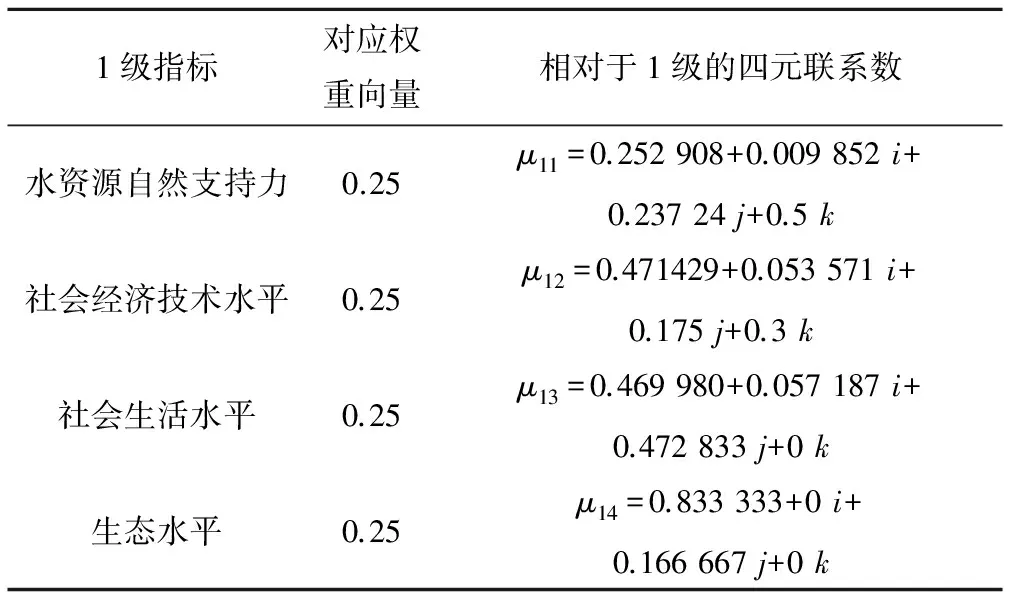
表2 一级指标相对于1级的四元联系数

将一级指标进行加权运算，用式(8)计算出总指标相对1级标准的四元联系数：

μ1=0.506 913+0.030 152i+0.262 935j+0.20k(10)

2级、3级标准的四元联系数可由以上原理得到：

μ2=0.750 828+0.014 297i+0.159 875j+0.075k

(11)

μ3=0.587 5+0.062 5i+0.1j+0.25k

(12)

根据计算结果，日照水资源承载能力无论是哪一级标准，其同一度均大于对立度，且相对于2级标准(中)的同一度与对立度之差最大。如果从三元联系数来考虑，则相对于2级标准的联系数最大，评价结果为2级，属于中等承载能力。按四元数来考虑，根据均分原则，在四元联系数中i的取值应位于三等分点处，[1/3,1] [1/3, -1/3] [-1/3,-1],令i=1/3，j=-1，k=-1，得到日照水资源承载力对于“1级”、“2级”、“3级”联系数分别为0.054 028、0.520 719、0.258 333，总指标的联系数为0.277 7，则评价日照水资源承载能力属于2级，处于中等水平状态。与文献[12]提出的模糊线性约束规划计算结果进行对比，通过计算可知，在来水保证率50%的情况下，日照市水资源可利用量不减少，且纳污能力不减少的情况下，日照市近期及十年内远期水资源承载能力随水效率因子及生态环境贡献(破坏)因子变动有一定范围波动，但总体处于中等以上承载能力水平。由此与文献[12]中采用由模糊分析法得到的日照水资源承载能力评价结果基本一致。