Hydrodynamic Characteristics in an External Loop Airlift Slurry Reactor
2016-03-22BianQingTangXiaojinHuLifengWangShaobingZhangZhanzhu
Bian Qing; Tang Xiaojin; Hu Lifeng; Wang Shaobing; Zhang Zhanzhu
(1. SINOPEC Research Institute of Petroleum Processing, Beijing 100083; 2. SINOPEC Qilu Branch Company, Zibo 255400)
Hydrodynamic Characteristics in an External Loop Airlift Slurry Reactor
Bian Qing1,2; Tang Xiaojin1; Hu Lifeng1; Wang Shaobing1; Zhang Zhanzhu1
(1. SINOPEC Research Institute of Petroleum Processing, Beijing 100083; 2. SINOPEC Qilu Branch Company, Zibo 255400)
Three different types of gas distributors were used in an external loop airlift slurry reactor to investigate the hydrodynamic characteristics. To predict the important hydrodynamic parameters, such as the total gas holdup, the slurry circulating velocity, the bubble size distribution, and the slip velocity between the gas phase and the slurry phase, the correlations are developed. The calculated results ft the experimental data very well. According to the infuence of the solid holdup on the bubble size, the fuid fow in the reactor can be divided into two regimes, while a 10% value is regarded as the critical solid holdup value. Whenεsis≤10%, the bubble size is determined by both the gas phase and the slurry phase. Whenεsis ≥10%, the bubble size is determined mainly by the slurry phase. By analyzing the relationship between the slip velocity and the gas holdup, the bubble coalescence plays a key role in the slurry reactor.
hydrodynamics, slurry bed, bubble size distribution, slip velocity
1 Introduction
To date, the investigation of the conversion of natural gas or coal to liquid fuels by the Fischer-Tropsch synthesis in slurry reactors have become a hot topic. But the design of large scale slurry reactors is still difficult because of the complexity of three-phase fow systems. Krishna and Sie suggested that the combination of small “hot” pilot plants and larger “cold-fow” engineering test maybe an acceptable approach to the design of large scale slurry reactors[1]. For larger scale “cold-fow” slurry reactors, the bubble hydrodynamics are evoking great interest in the fundamental research of gas-liquid-solid systems. Yang, et al.[2]reviewed the bubble measurement techniques and bubble dynamics in slurry reactors under the elevated temperature and pressurized conditions. Generally, the lognormal distribution can be used to describe the bubble size distribution in slurry reactors[3-4], and the population balance model can be used to calculate bubble breakage and bubble coalescence[5-7]. Behkish, et al.[8]found that increasing solid concentration could signifcantly increase the Sauter mean diameter of bubbles. For bubble swarms, the balance between the hydrodynamic force in the liquid and the surface tension can be used to calculate the maximum stable bubbles size,[9]but Luo, et al.[10]found that the gas inertia took the place of the liquid phase in the balance at high pressure.
By using the bubble size,d, the gas holdup,εg, and the slip velocity between the gas phase and the slurry phase,Vs, the drag coeffcient,CD, can be obtained by Equation 1[11]. In the literature[11-12], the relationship between the slip velocity and the dispersed phase holdup provides a criterion to divide the hydrodynamic regimes. When the slip velocity increases with the increase of the gas holdup, the fow in the slurry reactors is in the bubble coalescence regime. When the slip velocity decreases with the increase of the gas holdup, the fow in the slurry reactors is in the bubble dispersion regime.
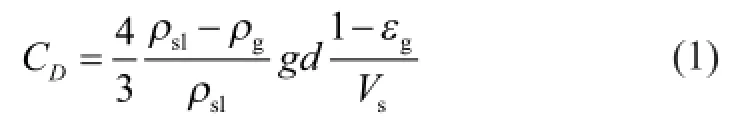
In this study, three types of gas distributors were used, respectively, in an external loop airlift slurry reactor at room temperature and under pressure. The influence of the superficial gas velocity and the solid holdup on the hydrodynamic characteristics was investigated.
2 Experimental
The experimental setup is shown in Figure 1. The external loop airlift slurry reactor is made of Plexiglass, and the total height of the reactor is 5 m. The riser is 3.4 m in height and 280 mm in diameter. The gas/slurry separator is 1.2 m in height and 420 mm in diameter. The diameter of the downcomer is 80 mm.

Figure 1 Experimental setup
Inside the slurry reactors the liquid phase and the solid phase are mixed so well that they can be taken as a uniform slurry phase. In the external loop of the airlift slurry reactor, the gas phase enters the riser from the gas distributor and is dispersed into bubbles. The bubbles go through the riser upwards and leave the reactor at top of the gas/slurry separator. In the downcomer, there are few bubbles so the density of the fluid in the riser is much lower than in the downcomer. Because of the density difference of fuids in the riser and the downcomer, the circulating fow of the slurry is formed.
Three types of gas distributors were used in the slurry reactor, including two types of pipe ring distributors and one sintered metal plate distributor. Distributor Ⅰ contains two pipe rings with 93 mm in inner pipe ring diameter and 186 mm in outer pipe ring diameter. The diameter of the pipe is 18 mm. At the top of the pipe rings, there are 40 holes, 2 mm in diameter. There are 10 holes on the inner pipe ring and 30 holes on the outer pipe ring, respectively, and the holes are uniformly located. By the DistributorⅠ, the gas phase can directly fow upwards in the reactor. The geometry of the Distributor Ⅱ is the same with that of the Distributor Ⅰ but its holes are at the bottom of the pipe rings. So the gas phase flows downwards from the Distributor Ⅱ in the reactor, and then turns up and goes through the reactor. The distributor Ⅲ is a sintered metal plate distributor, 3 mm in thickness and 10 μm in average hole diameter. There are 12 pieces of plates in the Distributor Ⅲ which are placed at regular intervals in an equilateral triangle. The diameter of each piece of plate is 20 mm.
The experimental system is filled with air-water-glass beads. The medium diameter of glass beads is 48.34 μm and the packing density is 1 402 kg/m3. The density of the slurry can be obtained by Equation 2. The viscosity of the slurry can be obtained by Equation 3[13].

The slurry circulating velocity is measured by the electrolyte tracer method[14]. The bubble size is measured by the dual conductivity probe based on the conductivity difference between the gas phase and the liquid phase[15-17]. Also, the conductivity probe method can measure the local gas holdup. By averaging the local gas holdup, the total gas holdup can be obtained. Then, the total gas holdup values are corrected by the manometric method (as shown in Equation 4).

3 Results and Discussion
3.1 Total gas holdup
As an example, Figure 2 shows the infuence of the solid holdup,εs, and the superficial gas velocity,ug, on the total gas holdup,εg, by studying the DistributorⅠ. It can be found thatεgincreases with the increase ofugand decreases with the increase ofεs. Equation 5 can be used to calculateεgwith an average deviation of less than 10%, and Figure 3 shows the comparison ofεgbetween the experimental data and the calculated results. Table 1 shows the correlations for calculatingεgapplicable to three dis-tributors.


Figure 2 In fl uence ofεs, andug, onεg(in Distributor Ⅰ)

Figure 3 Comparison ofεg,expandεg,cal(in Distributor Ⅱ)

Table 1 Correlations for calculatingεg
3.2 Super fi cial slurry velocity
Figure 4 shows the infuence of the solid holdup,εs, and the superficial gas velocity,ug, on the superficial slurry velocity in the riser,usl, by taking the Distributor Ⅱ as an example. It can be found thatuslincreases with the increase ofugand decreases with the increase ofεs. Equation 6 can be used to calculateuslwith an average deviation of less than 10%, and Figure 5 shows the comparison between the experimental data and the calculated results ofusl. Table 2 shows the correlation with the calculateduslfor three distributors.

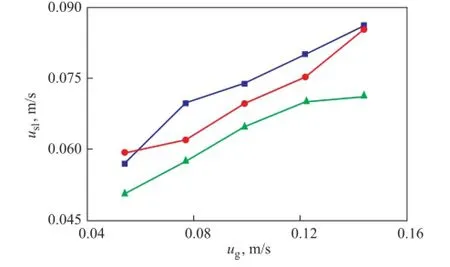
Figure 4 In fl uence ofεs, andug, onusl(in Distributor Ⅱ)

Figure 5 Comparison ofusl,expandusl,cal(in Distributor Ⅱ)

Table 2 Correlation with the calculatedusl
3.3 Bubble size distribution
Figure 6 shows the probability of number density function (DPF) of bubbles in the Distributor Ⅰ. The lognormal distribution is used to ft the experimental data. It can be found from Figure 6 that the bubble size distribution is a lognormal distribution as shown by Equations 6—8.



Figure 6 Bubble size distribution (in Distributor Ⅰ)
For the lognormal distribution, the two parametersdavandβshould be known to estimate the bubble size distribution. As an example, Figure 7 shows the infuence ofugandεsondavfor the Distributor Ⅲ. It can be found thatdavdecreases with the increase ofug. Whenεs≤10%,davdecreases with the increase ofεs. On the other hand, whenεs≥10%,davincreases with the increase ofεs. In this sense, a 10% value is the critical solid holdup. Whenεs≤10%, the viscosity of the slurry phase is relatively low and the size of bubbles are determined by both of the gas phase and the slurry phase. Whenεsis ≥10%, the viscosity of the slurry phase is high enough to enhance the effect of bubble coalescence. Therefore, the sizes of bubbles are mainly determined by the slurry phase.

Figure 7 In fl uences ofugandεsondav(in Distributor Ⅲ)
For the case ofεsbeing less than 10%, the influence of the gas phase and the slurry phase should be considered to predict the bubble size. Based on the theory of energy balance, the turbulent energy exerted on a bubble should be equal to the surface energy of the bubble so the Weber number is constant as depicted in Equation 10.

Based on Equation 9,davcan be obtained by Equation 11.

Thenucan be calculated by Equation 12[18].

By combining Equations 10 and 11, Equation 12 is obtained to calculatedavwhenεs<10%. Based on Equation 12, the energy dissipation,E, can be obtained by Equation 13.

By ftting the experimental data of three distributors, the parameterK1is 35 723. Figure 8 is the comparison between the experimental data and the calculated results ofdav.
Ifεsis more than 10%, the bubble size is mainly determined by the slurry phase. Based on Kolmogorov’s isotropic turbulence theory, the bubble size is proportional to the characteristic turbulent lengthlk, as shown in Equation 14.
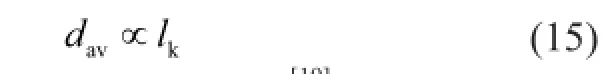
Thenlkcan be obtained by Equation 15[19].

Equation 16 can be obtained by combining Equations 14 and 15.

By ftting the experimental data of three distributors, the parameterK2is 1.098×106. Figure 9 is the comparison between the experimental data and the calculated results ofdav.
It can be seen from Figures 8 and 9 that the average deviation is less than 15%, which means that Equations 12 and 16 can be used to calculatedavwith good accuracy.
As an example, Figure 10 shows the comparison between the experimental data and the calculated results ofdavfor the Distributor Ⅲ. Equation 12 was used to calculatedavwhenεswas 0, and Equation 16 was used to calculatedavwhenεswas equal to 20%. Because 10% is the critical point, Equations 12 and 16 are both suitable for calculatingdavat this point, and then Equation 12 is used in this study. It can be found from Figure 10 that the calculated results ft the experimental data very well.

Figure 8 Comparison between experimental data and calculated results ofdav(atεs≤10%)

Figure 9 Comparison between experimental data and calculated results ofdav(atεs≥10%)

Figure 10 Comparison between experimental data and calculated results ofdav(in Distributor Ⅲ)
It is assumed that the relationship betweendavandβcan be expressed by Equation 17. By ftting the experimental data, Table 3 is obtained. For each value ofεs, Equation 17 is suitable for three distributors. As an example, Figure 11 shows the comparison of the bubble size distribution between the experimental data and the calculated results for the Distributor Ⅲ. It can be seen from Figure 11 that Equations 12, 13, 16 and 17 are good enough to calculate the bubble size distribution.


Table 3 Correlations betweendavandβ

Figure 11 Comparison between experimental data and calculated results of the bubble size distribution (in Distributor Ⅲ)
3.4 Slip velocity
The slip velocity,Vs, between the gas phase and the slurry phase can be obtained by Equation 18. As an example, Figure 12 shows the relationship betweenVsandεgin the Distributor II. It can be found thatVsincreases with the increase ofεg. From this point of view, the fuid fow in the slurry reactor is in the bubble coalescence regime[11].

Equation 19 is used to calculateVs. In Equation 19,u∞is the characteristic velocity of bubbles, which refers to the bubble terminal velocity in the quiescent liquid (or slurry) with the gas holdup being close to zero. The item (1-εg) is the effect of bubble dispersion and the item (1+nεg) is theeffect of bubble coalescence. By ftting the experimental data, Table 4 is then obtained.

Figure 12 RelationshipVsbetween andεg(in Distributor Ⅱ)


Table 4 Correlation forVs(in Distributor Ⅱ)
Figure 13 shows the comparison ofVsbetween the experimental data and calculated results in logarithmic coordinates for the Distributor II. It can be found that Equation 18 can predictVswith good accuracy.

Figure 13 Comparison between experimental data and calculated results ofVs(in Distributor II)
u∞can be calculated by Equations 20—22[20-11]. Becauseub1is much greater thanub2in this study, Equation 23 is obtained. By combining Equation 23 and Table 4,d0can be obtained.d0refers to the bubble diameter in the quiescent liquid (or slurry) with the gas holdup being close to zero, and then the bubble’s terminal velocity is equal tou∞. As an example, Table 5 shows the values ofd0and the experimental Sauter mean diameter,d32,expfor the Distributor II. It can be found thatd0is much smaller thand32,expunder the sameεs. So the fuid fow in the slurry reactor, which is in the bubble coalescence regime, is reasonable.


Table 5 Comparison betweend0andd32,exp(Distributor Ⅱ)
4 Conclusions
The hydrodynamic characteristics in an external loop airlift slurry reactor are investigated with three different types of gas distributors. The correlations are developed to calculate the hydrodynamic parameters, including the total gas holdup, the slurry circulating velocity, the bubble size distribution, and the slip velocity between the gas phase and slurry phase, which are obtained with good accuracy.
Based on the influence of the solid holdup,εs, on the average bubble size,dav, the fuid fow in the reactor can be divided into two regimes and 10% is the critical solid holdup value. Whenεsis ≤ 10%,davdecreases with the increase ofεsand the bubble size is determined by both the gas phase and the slurry phase. Whenεsis ≥ 10%,davincreases with the increase ofεs, and the bubble size is determined mainly by the slurry phase.
Upon analyzing the relationship between the slip velocity and the gas holdup, the bubble coalescence plays a key role in the slurry reactor.
Nomenclature
CD—drag coeffcient
Dr—riser diameter, m
d—bubble diameter, mm
d0—bubble diameter referring to u∞, mm
d32—Sauter mean bubble diameter, mm
dav—average bubble diameter in Equation 6, mm
δd—bubble diameter differential in Equation 8, mm
E—energy dissipation, m2/s3
f—number density function
g—acceleration due to gravity, m/s2
Δh—height difference, m
lk—characteristic turbulent length, mm
n—parameter in Equation 18
PDF—probability of number density function
Δp—pressure difference, Pa
Re—Reynolds number
u—velocity, m/s
Vs—slip velocity between the gas phase and the slurry phase, m/s
We—Weber number
Z—parameter in Equation 16
Greek letters
β—parameter in Equation 6
ε—phase holdup
ρ—density, kg/m3
μ— viscosity, Pa·s
σ— surface tension, N/m
Subscripts
cal—calculated
exp—experimental
g—gas phase
l—liquid phase
s—solid phase
sl—slurry phase
∞— refers to quiescent liquid (or slurry) with gas holdup being close to 0
Reference
[1] Krishna R, Sie S T. Design and scale-up of the Fischer-Tropsch bubble column slurry reactor[J]. Fuel Proc Tech, 2000, 64(1/3): 73-105
[2] Yang G Q, Du B, Fan L S. Bubble formation and dynamics in gas-liquid-solid fluidization—A review[J]. Chem Eng Sci, 2007, 62(1/2): 2-27
[3] Miyahara T, Hamaguchi M, Sukeda Y, et al. Size of bubbles and liquid circulation in a bubble column with a draught tube and sieve plate[J]. Can J Chem Eng, 1986, 64(5): 718-725
[4] Lage P L C, Esposito R O. Experimental determination of bubble size distribution in bubble columns: Prediction of mean bubble diameter and gas holdup[J]. Powder Tech, 1999, 101(2): 142-150
[5] Luo H, Svendsen H F. Theoretical model for drop and bubble breakup in turbulent dispersion[J]. AIChE J, 1996, 42(5): 1225-1233
[6] Lehr F, Millies M, Mewes D. Bubble-size distributions and flow fields in bubble columns[J]. AICHE J, 2002, 48(11): 2426-2443
[7] Wang T, Wang J, Jin Y. Theoretical prediction of flow regime transition in bubble columns by the population balance model[J]. Chem Eng Sci, 2005, 60(22): 6199-6209
[8] Behkish A, Lemoine R, Sehabiague L, et al. Gas holdup and bubble size behavior in a large-scale slurry bubble column reactor operating with an organic liquid under elevated pressures and temperatures[J]. Chem Eng J, 2007, 128(2/3): 69-84
[9] Hinze J O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion process[J]. AIChE J, 1955, 1(3): 289-295
[10] Luo X, Lee D J, Lau R, et al. Maximum stable bubble size and gas holdup in high-pressure slurry bubble columns[J]. AIChE J, 1999, 45(4): 665-680
[11] Simonnet M, Gentric C, Olmos E, et al. Experimental determination of the drag coefficient in a swarm of bubbles[J]. Chem Eng Sci, 2007, 62(3): 858-866
[12] Tang X, Luo G, Wang J. Mechanism analysis on the twophase flow characteristics in coalescence-dispersion pulsed-sieve-plate extraction columns[J]. Ind Eng Chem Res, 2008, 47(23): 744-754
[13] Thomas G D. Transport characteristics of suspension: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles[J]. J Colloid Sci, 1965, 20(3): 267-277
[14] Vial Ch, Poncin S, Wild G, et al. Experimental and theoretical analysis of axial dispersion in the liquid phase in external-loop airlift reactors[J]. Chem Eng Sci, 2005, 60(22): 5945-5954
[15] Boyer C, Duquenne A M, Wild G. Measuring techniques in gas-liquid and gas-liquid-solid reactors[J]. Chem EngSci, 2002, 34(16): 3185-3215
[16] Lo C S, Hwang S J. Local hydrodynamic properties of gas phase in an internal-loop airlift reactor[J]. Chem Eng J, 2003, 91(1): 3-22
[17] Zhang T, Wang J, Luo Z, et al. Multiphase fow characteristics of a novel internal-loop airlift reactor[J]. Chem Eng J, 2005, 109(1): 115-122
[18] Zhu S, Zhang B, Shen Z, et al. A study on two-phase fow characteristics in pulsed sieve plate column for liquid-liquid extraction[J]. Chinese Journal of Chemical Engineering, 1984, 3: 12-25
[19] Militaru R. Dimensional characterizations for homogeneous and isotropic turbulence[J]. Comput Methods Appl Mech Eng, 2001, 190(18-19): 2369-237
[20] Jamialahmadi M, Branch C, Müller-Steinhagen H. Terminal bubble rise velocity in liquids[J]. Chem Eng Res Des, 1994, 72(1): 119-122
[21] Tang Xiaojin, Hou Shuandi, Zhang Zhanzhu. Influence of gas density on hydrodynamics in a bubble column[J]. China Petroleum Processing and Petrochemical Technology, 2014, 16(1): 66-70
[22] Lü Chao, Zhang Zimu, Zhao Qiuyue, et al. Numerical simulation of enhanced oil-water separation in a threestage double-stirring extraction tank[J]. China Petroleum Processing and Petrochemical Technology, 2015, 17(4): 121-126
Received date: 2016-07-06; Accepted date: 2016-08-05.
Dr. Tang Xiaojin, Telephone: +86-10-82369270, E-mail: tangxj.ripp@sinopec.com.
杂志排行
中国炼油与石油化工的其它文章
- Effect of Magnetic Field on Tribological Properties of Lubricating Oils with and without Tricresyl Phosphate
- Preparation and Lubricating Properties of A New Antibacterial Emulsion Containing Nano-TiO2for Cold Rolling Strips
- Prediction of Coke Yield of FCC Unit Using Different Arti fi cial Neural Network Models
- An Extraction Process for Optimal Utilization of Naphtha Based on Molecule Management
- Microwave-Assisted Synthesis of Poly(Aspartic Acid-Itaconic Acid) Copolymer and Its Characterization
- Effects of Solution Chemistry Conditions and Adsorbent Surface Properties on Adsorption of Ni(II) on Laiyang Bentonite
