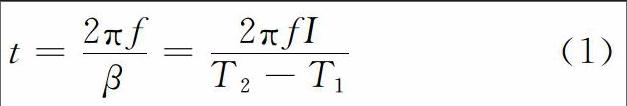振动压路机激振机构偏心块的设计优化
2016-03-22孔国华陈乐尧石明礼段乾坤
孔国华 陈乐尧 石明礼 段乾坤
摘要:为了提高振动压路机的作业性能和操作舒适性,对压路机激振机构内偏心块的转动惯量与静偏心矩的关系进行了研究,从理论上得出在静偏心矩一定的情况下,葫芦状的偏心块转动惯量最小,并利用软件仿真和试验验证了该结果。应用该种偏心块,能使压路机在不降低激振力和振动频率的情况下,提高起停振灵活性,从而提高压实路面的平整度。
关键词:振动压路机;偏心块;转动惯量;静偏心矩
中图分类号:U415.521文献标志码:B
Abstract: By researching the relationship between moment of inertia and eccentricity, it was found that the cucurbit shape of the eccentric block has the smallest moment of inertia when the eccentricity is fixed, and the result was validated by simulation and test. Application of this kind of eccentric block can improve the flexibility of vibration in the condition of not reducing the exciting force and vibration frequency of the roller, and as a result improve the smoothness of pavement.
Key words: roller; eccentric block; moment of inertia; eccentricity
0引言
振动压路机的工作原理是利用激振机构中偏心块旋转产生的离心力作用于钢轮上使钢轮振动,钢轮的振动能量传入被压实的路面上,从而实现路面的压实[12]。
在实际施工过程中,振动压路机是前进、后退交替压实,且在压实过程中,振动轮需要经历一次起停振阶段。振动轮的起振、停振时间对被压实路面及设备均有较大影响,如在起振和停振过程中,振动频率不断变化,激振力也不断变化,而在该过程中压路机的行走速度基本不变,如果起振、停振时间过长,会导致路面承受不稳定的激振力,从而影响路面的平整度和压实度;又如,由于压路机稳定工作时振动频率比整车固有频率高,因而起振、停振时间越长,振动频率超过压路机固有频率的时间就越长,会导致压路机的共振时间增长,从而影响路面的平整度,并且影响压路机的可靠性和操作舒适性。
因此在进行压路机的设计时,应保证在不降低压路机激振力和频率的前提下,尽量降低振动轮的起振、停振时间。
1设计需求分析
由于压路机工作时振动频率的选择与施工路面结构有关,本文不作相关论述,主要考虑在某一固定振动频率下,激振机构如何在不降低压路机激振力的前提下,尽量降低振动轮起振和停振的时间。
1.1振动轮起振、停振时间分析
全液压振动压路机工作时,激振机构受力如图1所示。
图中,T1为激振机构工作过程中的阻力矩;T2为振动马达提供的输出力矩;N为激振机构所受振动轴承的支撑力;F3为由于激振机构旋转而产生的离心力。由于激振机构重力相对于F3很小,本文忽略了激振机构重力的影响。
因此压路机起振时间为
式中: f为压路机的振动频率;β为激振机构的转动加速度;I为激振机构转动惯量。
由式1可知,起振时间t与f、 I成正比,与(T2-T1)成反比。在一般的设计过程中,振动频率f为选定值;T2与马达排量及振动系统压力有关;T1与压实对象、振动轴承、振动频率、激振力及润滑状况有关;I与激振机构的结构有关。因此,有效降低激振机构的转动惯量I对于降低压路机的起振时间,提高振动灵活性有直接的作用[3]。
1.2压路机激振力分析
压路机理论激振力为(即激振机构旋转产生的离心力)
F3=me(2πf)2(2)
式中:m为激振机构重量;e为激振机构重心距旋转中心的距离。
1.3设计需求简化
由式(2)可知,如果振动频率f不变,为了获得一定的激振力F3,激振机构的静偏心矩me必须相同。因此设计需求转化为如何满足在激振机构静偏心矩me一定的条件下,使其转动惯量I最小。
一般压路机激振机构由固定偏心块及活动偏心块组成,通过改变活动偏心块与固定偏心块的相位差可以获得不同的静偏心矩,从而获得不同的激振力。当活动偏心块及固定偏心块均满足me一定,I最小的条件时,激振机构整体达到设计要求。
假设活动偏心块及固定偏心块均采用钢板加工,因此偏心块厚度h与me及I均成正比,当单位厚度的偏心块达到设计要求后,具有一定厚度h的偏心块也达到设计要求,即:实际静偏心矩me×h不变的情况下,实际转动惯量I×h为最小。因此本文只需考虑对单位厚度偏心块的形状进行优化,获得的最优偏心块形状即可推广到具有一定厚度的偏心块。
2偏心块形状曲线优化
2.1提出目标函数
传统压路机激振机构中偏心块的形式主要为半圆形或扇形[3],如图2所示。
由于振动压路机偏心块均绕中心振动轴旋转,且实际偏心块的设计一般都采用对称结构,设旋转中心为原点,对称中心为x轴,因此可以先考虑位于第1、2象限的偏心块部分,静偏心矩及转动惯量的计算均相对于原点。
基于以上条件,设一任意偏心块处于第1、2象限内,与x轴相交的外轮廓曲线方程为
该曲线如图3所示。该曲线与x轴所围成的区域即所要求的偏心块形状的一半,由于实际偏心块相对于x轴对称,因此偏心块相对于原点的静偏心矩me0=2mex,且
图3任意偏心块位于第一、二象限内外轮廓曲线
式中:mex为所求区域相对于原点的静偏心矩在x轴上的分量;ρ为偏心块单位面积的质量。
该区域相对于原点的转动惯量为
因此所求的目标函数可以表示为
当满足mex=K时,使I0 最小的函数:r=f(θ),(0≤θ<π)。
其中K为根据压路机所需的激振力、激振频率得出的常数,计算方式如下
式中:F为压路机标定的激振力。
2.2最优曲线求取
在该曲线上假设有一点Ar,θ(见图4),其质量为d2m,其相对于原点的静偏心矩在x轴的分量为
dmex=rcos θdm(7)
相对于原点的转动惯量为
令:dI0dmex=r2dmrcos θdm=rcos θ=C
式中:C为常数。
则有
r=Ccos θ,(0≤θ<π)(9)
该方程代表的曲线为经过原点(0,0)及(C,0)点,且圆心在x轴上、半径为C2的圆,如图4所示。
该曲线上的任何点均满足
dI0=Cdmex=Cxdm(10)
经计算机仿真得出,该曲线即为所求的最优曲线,下面将对该结论进行证明。
2.3证明
设经过点(0,0)、(C0,0),圆心在x轴上的半圆所包含的区域为设计区域S,其相对于原点的静偏心矩在x轴的分量为me0x,相对于原点的转动惯量为I00。
如图5所示,假设位于设计区域S外,有一区域B(xj,yj)在第一象限内与区域S相邻,其相对于原点的静偏心矩在x轴的分量meBx=∫Bxjdm,相对于原点的转动惯量IB0=∫BdIj。
由公式(10)可推出,区域B相对于原点的转动惯量
如果将区域B(xj,yj)加入区域S内,为了满足区域S相对于原点的静偏心矩一定的要求,需要从区域S内删除一块区域,假设为A(xi,yi),以抵消加入区域B所增加的静偏心矩,因此区域A(xi,yi)相对于原点的静偏心矩在x轴的分量满足
由公式(10)可推出,区域A(xi,yi)相对于原点的转动惯量
由于区域A包含在设计区域内,区域B在设计区域外,因此Ci 因此图5所示阴影部分所组成的新区域满足:me0x+meBx-meAx=me0x,即与设计区域S相对于原点的静偏心矩在x轴的分量相同;相对于原点的转动惯量为:I00+IB0-IA0>I00,即大于设计区域S相对于原点的转动惯量。因此在该条件下,设计区域S满足静偏心矩一定,转动惯量最小的要求。 如图6所示,假设位于设计区域S外,有一区域E(xk,yk)在第二象限内与区域S相邻,其相对于原点的静偏心矩在x轴的分量meEx=∫Exkdm,相对于原点的转动惯量IE0=∫EdIk=∫ECkd(mek)=∫ECkxkdm。如果将区域E(xk,yk)加入区域S内,为了满足区域S相对于原点的静偏心矩在x轴的分量一定的要求,必需在第一象限再增加一块区域D(xl,yl),由于增加了两块区域,此时相对于原点的总转动惯量必定大于I00。即该条件下设计区域S也满足静偏心矩一定、转动惯量最小的要求。 由以上证明可知,在第一、二象限内,满足相对于原点的静偏心矩在x轴的分量一定的情况下,经过原点,且圆心在x轴上的半圆所围成的区域相对于原点的转动惯量最小,即式9所代表的曲线为所求的最优曲线。 该曲线相对于x轴对称的曲线为:r=Ccos θ,(π≤θ<2π),因此所求理想的整个偏心块的最优轮廓曲线如图7所示。 r=Ccos θ,(0≤θ<2π)(15) 3软件计算 式(15)所代表的曲线为理论最优曲线,该曲线没有考虑材料的装配、加工、承载等因素,由于偏心块工作时必须绕原点旋转,因此实际设计偏心块时,原点处必须包围一定厚度的材料,以保证偏心块绕原点旋转时,材料在离心力的作用下不会失效。 图8为某压路机偏心块实际形状及尺寸,利用Pro/e对该零件进行分析,其相对于原点的静偏心矩me1=319.5 kg·mm;相对于原点的转动惯量I1=6.26×104 kg·mm2;材料重量m1=787 kg。 如果采用另一种常用的扇形偏心块,为了保持恒定的静偏心矩,在厚度一定的情况下,需求外形尺寸如图9所示。 经Pro/e对该零件进行分析,其相对于圆点的静偏心矩me2=320.1 kg·mm;相对于圆点的转动惯量I2=5.72×104 kg·mm2;材料重量m2=7.41 kg。 如果采用本文推出的最优偏心块形状,偏心块主体轮廓必须为经过原点,且圆心在x轴上的圆(见图10中位于第1象限和第4象限内R148.5所代表的圆),为保持与上述两种形状的偏心块相对于原点的静偏心矩相同,在相同厚度的情况下,需求外形尺寸如图10所示。 经Pro/e对该零件进行分析,其相对于原点的静偏心矩me0=319.5 kg·mm;相对于原点的转动惯量I0=5.26×104 kg·mm2;材料重量m0=656 kg。 对比以上数据有 me0=me1=me2;I0=0.84I1=092I2;m0=0834m1=0885m2。 由压路机起振时间公式t=2πfIT2-T1可知,在保证压路机振动频率、泵和马达型号、轴承型号及负载不变的情况下,使用这3种不同偏心块的压路机的起停振时间存在以下关系:t0≈084t1≈092t2。 因此,在保证偏心块相对于原点静偏心矩不变的情况下,对偏心块形状进行优化后,使压路机起振时间缩短为原来的84%;且偏心块质量也降低为原来的83.4%,既节约了材料,又提高了偏心块的灵活性。 4试验验证 本公司同吨位系列中有2台不同的压路机,其中压路机A的激振机构采用半圆形偏心块,且振动轴直径较大;压路机B的激振机构采用了优化后的偏心块,且对整体结构进行了改进,将原来1根较粗的振动轴改为2根较细的振动轴串联,在不影响振动轮激振力的情况下,使激振机构的转动惯量得到了大幅减小。理论上振动轴直径减小引起的转动惯量的减小及偏心块形状优化后转动惯量的减小将共同作用,降低压路机起停振时间。 图11为压路机A的振动液压系统压力曲线图,图12为压路机B的振动液压系统压力曲线图,试验时2款压路机的的激振力、振动频率、马达排量及压实对象基本相同。 由图11、图12可以看出,起振时2款压路机振动液压系统压差都是32 MPa左右,停振时压差约为25 MPa,压路机A激振机构振动频率从零加速到设定值所用的时间约为52 s,从设定值减速到零所需的时间约为44 s。压路机B对应的上述时间分别为2.6 s和2.4 s,即压路机B的起振时间仅为压路机A的50%,停振时间仅为压路机A的55%。 该试验结果说明采用本文所述的激振机构,能够使振动系统变得更加灵活,起振、停振时间更短。 5结语 由以上理论分析和试验数据所得出的结果可得出以下结论。 (1) 偏心块理论最优轮廓曲线方程为:r=Ccosθ,(0≤θ<2π),代表的曲线为经过原点,且圆心在x轴上的圆。 (2) 与传统半圆形偏心块及扇形偏心块相比,在静偏心矩相同的条件下,设计的葫芦状偏心块转动惯量及质量均最小,既提高了压路机激振机构的振动灵活性,又能节省材料。 (3) 试验验证采用优化后的偏心块及激振机构,能有效降低压路机的起振、停振时间,从而有利于提升压实路面的平整度。 参考文献: [1]尹继瑶.压路机设计与应用[M].北京:机械工业出版社,2000. [2]胡春军,王华君.探析振动压路机的工作装置[J].工程机械,2007,38(9):1316. [3]万汉驰,胡春军.振动压路机振动轴结构浅析[J].建筑机械,2001(12):3435. [责任编辑:杜卫华]