对几种不常见刚体转动惯量的研究

周瑞雪

（贵州师范大学物电院，贵州 贵阳 550001）

引言

对于我们常见到的刚体，如均匀细棒、圆盘、圆环、圆柱等，教科书中已给出其转动惯量的结论，我们也可以根据转动惯量的定义计算出来，但对于另外一些刚体，如椭圆盘、球体、长方体、六面体等这些刚体，其转动惯量的推导和计算教科书并没有给出，有些刚体转动惯量的计算上也有一定的难度，本篇文章将对这些刚体的转动惯量在理论上进行一些研究，计算出它们的转动惯量.

1 球体的转动惯量

质量为m，半径为R 的均匀球体，计算通过中心轴的转动惯量.

方法：分割积分法［1］

如图1把球分成很多的薄圆盘，薄圆盘的半径为

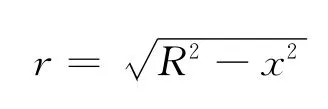
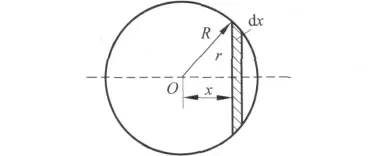
图1

质量为

dm =ρdV =ρπr2dx

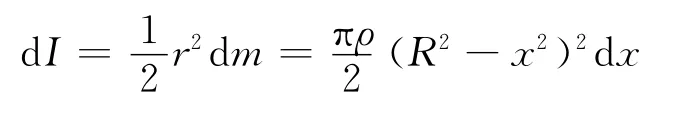
整个球的转动惯量为

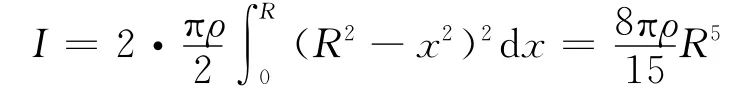
球的质量

得到结果

2 椭圆盘的转动惯量

质量为m 的均质薄椭圆盘，其长半轴为a，短半轴为b，计算其对x、y、z轴的转动惯量.

方法：质量投影法［2］

（1）首先计算对x 轴的转动惯量

如图2所示，将椭圆盘向y 轴投影得到长为2b的线段，质量仍为m，但质量非均匀分布，其质量线密度为

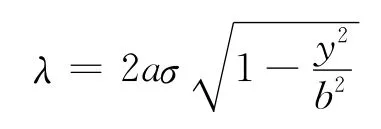
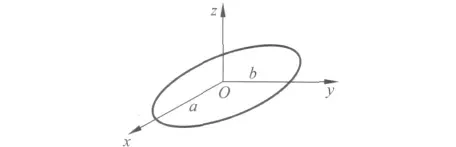
图2

那么，长为2b的线段对x 轴的转动惯量即系均质椭圆盘对x 轴的转动惯量.

计算为

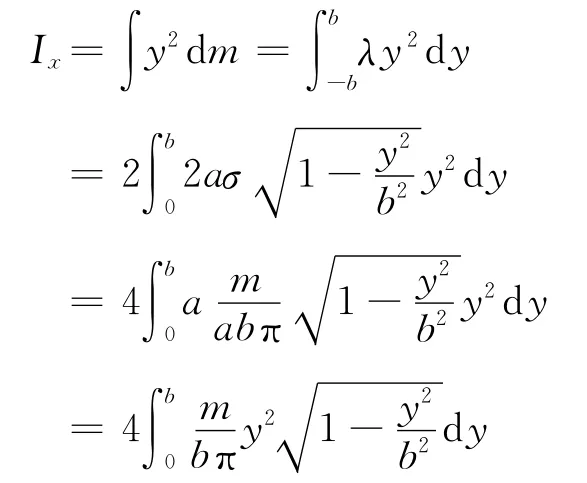
（2）数学计算［7］

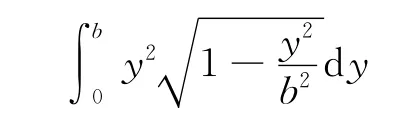
令

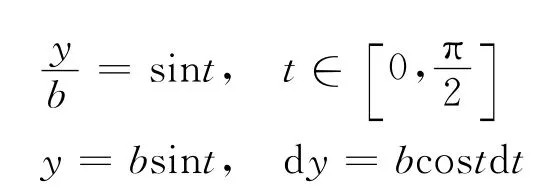
于是有

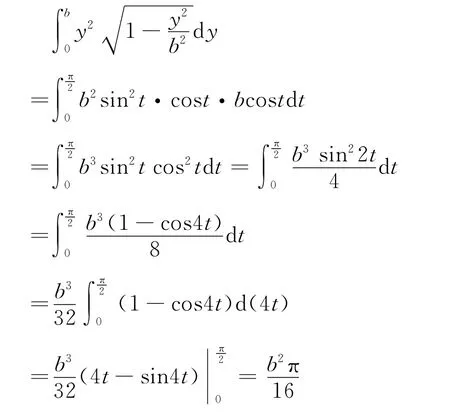
（3）结论

②同理得均质椭圆盘对y 轴的转动惯量为

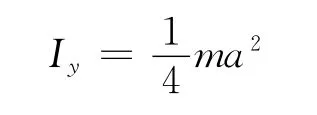
③利用正交轴定理得出对z轴的转动惯量为

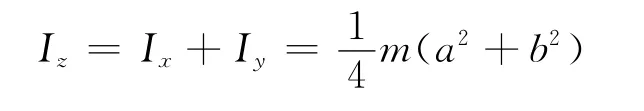
3 均质六面体的转动惯量

如图3所示，已知六面体的长为a、宽为b、高为c，其质量m 均匀分布，分别计算六面体对过质心 的x 轴、y 轴、z轴 的 转 动 惯 量.

图3

方法：质量投影法［3］

（1）首先计算对z轴的转动惯量

将六面体向Oxy 平面投影得到长为a 宽为b的与z 轴垂直的矩形平面s，其质量仍为m 且均匀分布，这样就把六面体对z 轴的转动惯量转化为均质矩形平面s对z 轴的转动惯量；再将平面s向y 轴投影，得到长为a 的线段（细杆），其质量仍为m 且均匀分布，线段a对x 轴的转动惯量为

即为平面s对x 轴的转动惯量.

（2）同理得平面s对y 轴的转动惯量为

（3）因此平面s对z 轴的转动惯量为

此即均质六面体对z轴的转动惯量.

（4）同理得均质六面体对x 轴、y 轴的转动惯量

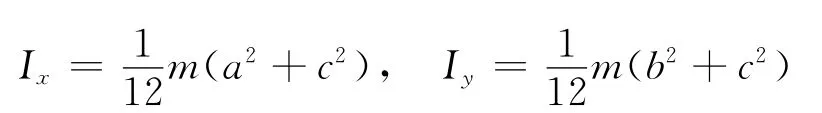
（5）讨论 当a＝b＝c＝l时，

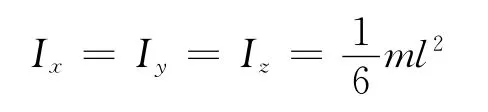
此即均质六面体转化为均质正六面体.

4 均匀长方形薄板的转动惯量

已知长方形薄板的长为a、宽为b、质量为m，转动轴为其对角线，计算其转动惯量.

方法：定积分法［5］

如图4所示，取对角线为x 轴，原点为O 和它垂直的直线为y 轴，令σ为薄板的面密度.

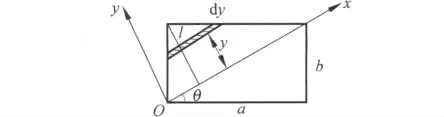
图4

取一长方形窄条，长为l，宽为dy，由转动惯量的定义得到绕对角线（x 轴）转动的转动惯量为

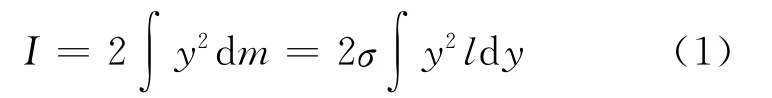
将l代入式（1）得

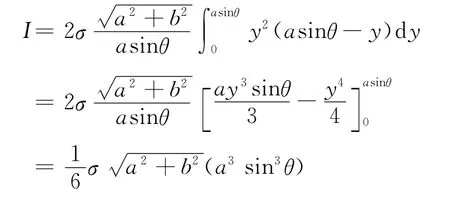
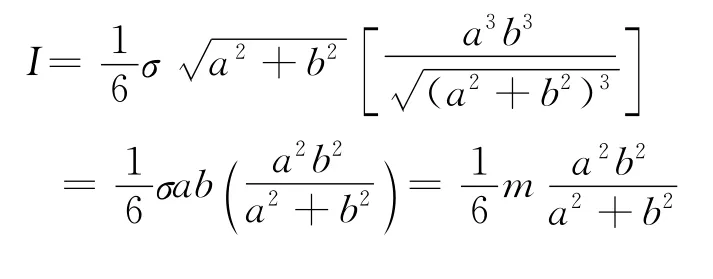
5 空心立方体柱的转动惯量

如图5所示，已知空心立方体（即由四块正方形薄板构成），质量为m，边长为2R，转轴通过重心并和图面垂直，计算其转动惯量.

方法：为了求四薄板空心立方体绕过它的重心并垂直图面的轴的转动惯量，先求一块板绕该轴的转动惯量.

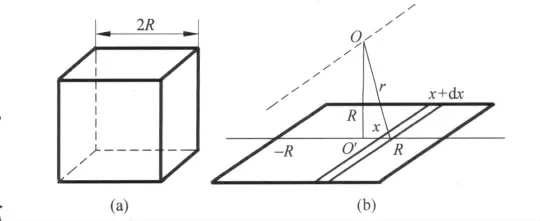
图5

距O 轴的距离是

r2＝R2＋x2

所以，此窄条绕O 轴的转动惯量是

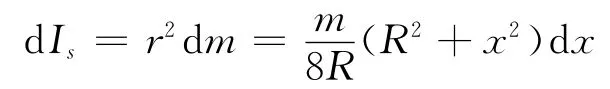
因此整个薄板绕O 轴的转动惯量是

结论：由于四块薄板对O 轴是对称的，所以整个立方体对O 轴的总的转动惯量为

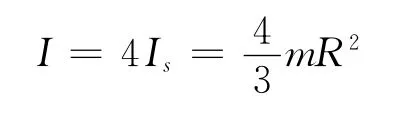
6 结束语

本文从转动惯量的定义出发，采用了分割积分法，质量投影法等方法，计算了椭圆盘、六面体、正立方体，空心立方体、转轴在对角线上的长方形薄板等几种不常见刚体的转动惯量，给出了教材中没有的计算方法，对同行和研究这方面的学生有一定的借鉴作用.

［1］［美］F.W.Sears.大学物理学（第一册）［M］.郭泰运译.人民教育出版社，1979.274～278

［2］王永超.刚体转动惯量的质量投影法［J］.大学物理，2010，9

［3］漆安慎，杜婵英.普通物理学教程：力学［M］.北京：高等教育出版社，2005.222～226

［4］徐德，刘聚成，袁贞丰.大学物理学习题解答［M］.北京：人民教育出版社，1989.319～324

［5］周衍柏.理论力学［M］.北京：人民教育出版社，1982

［6］马文蔚.物理学（上册）［M］5版.北京：高等教育出版社，2008.104～111

［7］华东师范大学数学系.数学分析（上册）［M］3版.北京：高等教育出版社，2001.224～225