“任性”表达:儿童数学思维的理性观照
2016-03-21张锦
【摘要】儿童天生是诗人和哲学家。数学教学应当关注儿童思考问题的视角及其对数学现象的理解和表达方式,不必过分苛求他们对知识点进行完美的表述。儿童的“任性”表达作为其数学思维的呈现方式,充盈着智慧,彰显着价值,闪耀着人性。
【关键词】“任性”表达;数学思维;理性唤醒;理性构建;理性自觉
【中图分类号】G623.5 【文献标志码】A 【文章编号】1005-6009(2016)06-0024-03
【作者简介】张锦,江苏省淮安市实验小学(江苏淮安,223000),一级教师。
一、“任性”一些又何妨?
新课改以来,尤其是新课标实施以来,人们越来越关注儿童的“学”,关注“以生为本”,关注儿童的长期可持续发展。但是,我们也应该看到,在数学课堂上,儿童自由表达的时空仍然受到比较大的限制。
1.争论不休的“规定”。每到备课季,教研组的老师们都会为“鸡毛蒜皮”的细节争得面红耳赤。比如:“6∶05”究竟怎么读?甲说:“严格按照教参,读作‘6时零5分。”乙说:“为什么不能读作‘6时过5分呢?”争论不灭亦不休。
2.追求完美的“表达”。一教师执教苏教版五下《圆的认识》,教到半径、直径等概念时,教师用手指着“圆上”,引导学生说:“这叫圆——”面对学生思维短路、表述不畅等情况,教师干脆打断学生的回答,说:“这叫圆上,大家齐读——经过圆心,两端都在圆上的线段……”
儿童与数学的相遇应该是美好的。词人纳兰性德描绘了“人生若只如初见”的意境,我们不妨将儿童学习数学的过程视作他们与数学“初见”的过程。这样说来,观照当下的数学课堂,让学生的表达“任性”一些又何妨?
二、数学课堂中“任性”表达的价值探寻
表达是将思维所得的成果用语言反映出来的一种行为。在数学教学中,笔者更愿意将“表达”理解为:数学思维成果以广义的语言形式呈现出来。聚焦课堂,这种表达方式可能是口语式的、图画式的、操作式的……在表达前面冠以“任性”二字,并非简单地附庸时尚,而是从儿童和学科的角度,还原他们学习的真实状态。
1.尊重人性:关于本原,关于未来,关于价值观照的哲学视角。周国平曾说过:“孩子天生是诗人和哲学家。”童年是一个独特的生命阶段,每个儿童都是一个完整的生命个体,有自己的哲学。基于儿童“任性”表达的数学课堂,教师理应对儿童抱有敬畏之心、谦逊之心,精心呵护他们的发现、表达和成长。
2.顺应天性:关于成长,关于生命,关于理性彰显的审美意蕴。尼采说:“只有作为审美现象,人世的生存才有充足的理由。”变封闭、被动、个体、静态的表达为开放、主动、集体、动态的表达,就是基于儿童生命发展的教学诉求。教师应注意赋予课堂“任性”表达的时空,为儿童的精彩成长提供可能。
3.彰显个性:关于自主,关于思考,关于素养提升的教育诠释。《义务教育数学课程标准(2011年版)》指出:学生学习应当是一个生动活泼的、主动的和富有个性的过程。儿童的“任性”表达在一定程度上是基于自主建构和个性思考的,这种思考可能是灵光一现的,也可能是经过深思熟虑的。在数学表达的过程中,学生借助抽象和半抽象的图像、符号等载体,完成一次次“破茧飞翔”的思维之旅。
三、数学课堂中“任性”表达的实践策略
(一)基于“任性”表达:指向儿童数学思维的理性唤醒
1.沿着“精神实体”的目标展开——“是什么”“为什么”“怎么样”。
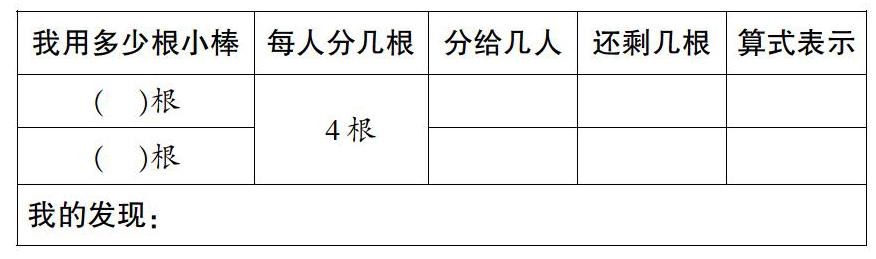
数学教育家弗赖登塔尔曾指出:数学教学目标一个叫精神实体,一个叫实体。实体解决的是“是什么”的问题,精神实体则沿着“为什么”“怎么样”的路径展开。例如:苏教版二下《有余数的除法》一课的教学重点,是研究除数和余数的关系,我设计了如下学习单:
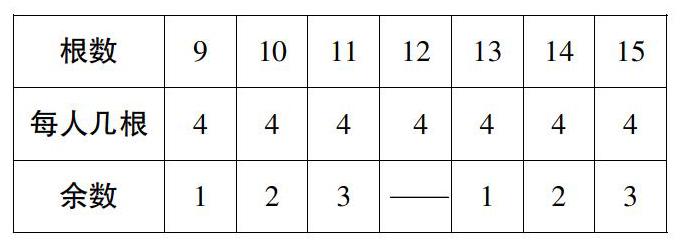
表格承前启后,及时巩固例1,又为例2做好了准备。在教学例2时,通过操作9—15根小棒研究除数和余数的关系,板书则借鉴了教材的样式。
学生的“任性”表达由此开始。(1)争执阶段——“是什么”:在说12的余数时,学生出现了0和4的争执,讨论后一致认为余数是0(更准确地说,是没有余数);(2)延伸阶段——“怎么样”:16根,余数是多少呢?(3)发现阶段——“为什么”:余数会是5、8、9吗?会是4吗?3呢?余数可能和谁有关呢?有什么关系?有的学生说“余数不能比4大”,有的学生说“余数要比4小”,还有的学生说“除数是4,余数就固定了”……
2.基于“朴素理解”的形式推进——“从哪里来”“到哪里去”。
北京教育学院刘加霞教授说:“数学教学应该行走在‘朴素理解和‘形式化之间。”在数学教学中,基于朴素理解的表达应带有儿童特质,但又不能让其失去数学的学科特点。例如:教学苏教版三上《分数的认识》时,我们可以让学生自主理解“二分之一”,借助饼形图、线段图、实物图等表征方式,最终指向分数的数学意义。教师应注意让学生经历知识发生、发展的过程,既要感受到知识“从哪里来”,又要知晓“到哪里去”,顺着这样的思路延伸,构建理性的数学学习生活将成为贯穿课堂的主线,儿童的数学思维将得到发展。
(二)延伸“任性”表达:指向儿童数学学习的理性建构
1.建立儿童认知与学科体系的联系,凸显数学学习的哲学意蕴。
皮亚杰说:“儿童的数概念不是成人能直接教会的。”儿童有时会有这样一种感觉:老师讲的不是我们需要的,我们需要的老师都没讲。在儿童的认知与学科体系之间,往往存在着断层或鸿沟。教师应注意挖掘并延伸儿童“任性”表达的资源及其价值,帮助他们有效建构认知体系。例如:教材在编排苏教版六上《百分数的认识》时,从投篮比赛引入,“巧合”的是,这几个分数的分母分别是5、20、25,化成分母是100的分数后就变成百分数了。一个学生追问:“万一分母不是5、10、25这样的数,百分数还能这样变过来吗?”顺着这个追问往下走,很快就能接近百分数的本质了。
2.建立学习直觉与数学理性的联系,凸显数学学习的审美意蕴。
儿童的“任性”表达往往包含着数学学习的直觉。美国数学家库朗指出:直觉,这种难以捉摸、充满活力的力量,始终在创造性的数学中起作用,甚至推动和引导最抽象的思维过程。例如:苏教版二下“两、三位数的加法和减法”单元有这样一道例题:车上原来有34人,到站后有15人下车,又有18人上车,离站时车上有多少人?学生列出了算式,分别是:(1)34-15+18=37(人);(2)34-15=19(人),19+18=37(人);(3)34+18-15=37(人);(4)18-15=3(人),34+3=37(人)。对于第四种算式,学生解释:15人下车,位置空出来,18人中有15个人补坐上去,还剩下3人,也就相当于多了3人。学生一个简单的比方、一种形象的表达,也许强过教师的百般引导,这其中,学生的数学思考方式是需要教师倍加珍视的。
3.建立数学发现与核心知识的联系,凸显数学学习的教育意蕴。
数学教育家波利亚发现,数学有两个方面:用欧几里得方式提出的数学是一门系统的演绎科学,但在创造过程中的数学是实验性的归纳科学。鼓励儿童“任性”表达的数学课堂应以“核心知识”为主线,在数学发现中让学习真实地发生。例如:教学苏教版二下“近似数”,借助数轴,学生发现,越往左边越接近500,越往右边越接近600,这些数都以一个数为界限,那就是550。李同学突然提问:“为什么要把550作为分界线,而不是其他数呢?”一石激起千层浪:“5000约等于几千?”有的学生说:“5000≈6000。”大家马上否定:“5000怎么会约等于6000呢?”有学生说:“5000有近似数吗?”在美妙的数学发现中,学生又初步表达了对使用“近似数”的感觉:“买东西大概需要多少钱”“旅游的时候大约走了多少千米”等都会用到。将数学发现与核心知识联系起来,富有趣味和意义。
(三)提升“任性”表达:指向儿童数学学习的理性自觉
1.让“任性”表达与数学语言有效接轨,学会数学地思维。
北京师范大学石中英教授在《教育哲学导论》一书中阐释:“人的发展,就其根源来说,不是一个外在的规则或控制过程,而是一个内在的觉醒或成长过程。”在某种意义上,学生的“任性”表达与其思维发展水平有着不可分割的关系。在教学中,教师应巧妙地将儿童形象化的、事例化的表达与数学语言接轨,哪怕是隐性接轨也是非常有必要的。例如:苏教版二下“角的初步认识”单元有一道关于“用一副三角尺拼出不同的角”的思考题。有的学生将“拼”理解为“两个三角尺的叠加”,有的学生“拼”出了符合要求的角却答非所问。教师引导学生将他们的错误理解各个击破后,学生很容易就理解了“拼”就是“顶点重合,一条边重合”。引领儿童转换数学语言的过程,也是帮助他们转换数学思维的过程。
2.让“任性”表达与数学理解巧妙联通,实现思维数学化。
儿童的“任性”表达是基于数学素材,通过数学思考,指向数学思维的过程。教师应注意借助对比、推理、猜想、验证等方法,将儿童的思维表达与数学思考巧妙连接。例如:教学苏教版二下“有余数的除法应用题”,我对教材进行整合,呈现了两道对比题:(1)10个磁性圆片,每人4个,最多可以分给几个人?(2)10个磁性圆片,每个袋子装4个,需要准备几个袋子?对比之后,学生各抒己见:“人家会不高兴的,袋子还需要准备一个”“你买了10个苹果,还剩下2个不能不拿就走,还需要一个袋子装走”……对比中透露出学生数学思考的力量,初步的思维模型也在他们头脑中浮现。
3.让“任性”表达与数学思考高效契合,促进思维自觉化。
在课堂的互动环境中,在表达与思考之间建立起联系,促进个体自主建构,可行而且有必要。例如:苏教版二下“两、三位数的加法和减法”单元有这样一道思考题:赵强家养的鸡比鸭多30只,后来又买来30只鸡和45只鸭。现在是鸡多还是鸭多,多多少只?教学用书提供了两种思路:一种是补差法,一种是假设法。小王同学假设鸭有0只,鸡有30只。围绕假设,学生的思考高度展开。教师问:“可以设30和60吗?”学生认为可以,还可以设15和45,还有人说设1030和1060,在对假设的数据进行遴选时,学生进行了优化。有的学生还说“假设鸡比鸭多25只”,被直接否定:“题目里说的是多30只,条件不可以改变。”学生辩解:“0和30题目里也没有啊。”大家认为:就是因为没有才去假设,但不能改变题目的意思。通过几轮思考,学生的表达层层深入,思维也变得敞亮起来。
“不忘初心,方得始终。”教师应悉心呵护学生学习数学的“初心”,让数学思维在学生“任性”表达的过程中逐渐被唤醒,让学生“诗意地栖居”,绽放“活泼泼的生命”,那将是一种美妙的向往和追求!
【参考文献】
[1]许卫兵.简约数学教学[M].南京:江苏教育出版社,2011.
[2]G.波利亚.数学与猜想:数学中的归纳和类比[M].李心灿,王日爽,李志尧,译.北京:科学出版社,2012.
[3]G.波利亚.数学与猜想:合情推理模式[M].李志尧,王日爽,李心灿,译.北京:科学出版社,2013.
[4]亲近母语研究院.儿童与哲学[M]北京:接力出版社,2012.
[5]刘晓东.儿童精神哲学[M].南京:南京师范大学出版社,2003.
注:本文获2015年江苏省“教海探航”征文竞赛一等奖,有删改。
