基于土壤物理基本参数的土壤导热率模型

苏李君，王全九，王　铄，王卫华（1. 西安理工大学理学院，西安 71005；　2. 西安理工大学水利水电学院，西安 71008；. 商洛水务局，商洛 726000；　. 昆明理工大学现代农业工程学院，昆明 650500）



基于土壤物理基本参数的土壤导热率模型

苏李君1，2，王全九2※，王铄3，王卫华4
（1. 西安理工大学理学院，西安 710054；2. 西安理工大学水利水电学院，西安 710048；3. 商洛水务局，商洛 726000；4. 昆明理工大学现代农业工程学院，昆明 650500）

摘要：土壤物理基本参数是影响土壤导热率的重要因素，为了获取土壤的颗粒组成、有机质含量与土壤导热率计算模型中参数之间的关系，该文分析了陕西省9个地区的土壤质地对土壤导热率的影响，对不同土壤导热率估算模型的准确性进行评价，并在Côté-Konrad模型和Lu-Ren模型的基础上，建立了基于土壤物理基本参数的改进模型，结果表明：改进的Côté-Konrad模型与改进的Lu-Ren模型可以用来拟合不同质地的土壤导热率，且具有较好的拟合精度，决定系数R2均在0.92以上，相对误差（relative error，Re）均低于9.6%；对于砂粒含量或粉粒含量较高的土壤导热率，改进的Côté-Konrad模型模拟结果的均方根误差（root-mean-square error，RMSE）≤0.1183、R2≥0.9259以及Re≤9.55%，均优于Côté-Konrad模型、Lu-Ren模型和改进Lu-Ren模型；对于砂粒和粉粒含量均较低的土壤导热率，改进Lu-Ren模型模拟结果的RMSE ≤0.0815、R2≥0.9326，Re≤8.21%，均明显优于其他3种模型。两种改进的模型分别建立了模型参数与颗粒组成、有机质含量之间的关系，能够更加详细描述土壤物理基本参数与导热率之间的关系，并且针对不同的土壤质地，选取合适的改进模型能够更加准确地计算土壤导热率。

关键词：土壤；模型；含水率；土壤物理基本参数；土壤导热率模型；改进模型

苏李君，王全九，王铄，王卫华. 基于土壤物理基本参数的土壤导热率模型[J]. 农业工程学报，2016，32（2）：127－133.doi：10.11975/j.issn.1002-6819.2016.02.019http://www.tcsae.org

Su Lijun， Wang Quanjiu， Wang Shuo， Wang Weihua. Soil thermal conductivity model based on soil physical basic parameters[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2016， 32（2）: 127－133. （in Chinese with English abstract）doi：10.11975/j.issn.1002-6819.2016.02.019http://www.tcsae.org

0　引　言

土壤导热率是土壤热性质的重要指标之一，也是土壤的水、热、溶质耦合数值模型的重要参数，如何快速准确估算土壤导热率成为研究土壤热性质的主要内容之一[1]。目前，国内外学者提出了很多间接估算模型，用于描述导土壤热率与土壤质地、容重、含水率、有机质之间的关系[2-10]，常用的间接估算模型有两类：经验模型[2-3]和半理论模型[4-7]。经验模型主要有Chung-Horton模型和Campbell模型，分别建立了导热率与土壤含水率之间的关系，这类模型计算简单，但由于不同地区土质的差异，模型参数取值存在不确定性，使得计算值与实测值误差较大[8]。半理论模型主要有Johansen模型、Côté-Konrad模型和Lu-Ren模型[9]，分别建立了导热率与土壤饱和度之间的关系，这类模型有一定理论基础，且针对不同土壤质地给定了模型参数值，但对于不同的土壤颗粒和有机质含量，模型参数取值也不同，导致了模型应用具有一定的局限性。总的而言，不同模型各具优缺点，但不同类型土壤的颗粒组成、有机质含量对模型参数取值的影响仍需进一步深入研究。

本文采用热脉冲方法测定原状土土壤导热率，分析了土壤颗粒组成对导热率的影响，建立了导热率与饱和度、容重、土壤颗粒组成和有机质之间的关系，提出了改进的Côté-Konrad模型和改进的Lu-Ren模型，为简单、快速获取土壤导热率提供参考。

1　材料与方法

1.1试验土样

本文试验数据分别来自陕西省神木、米脂、安塞、宜川、洛川、长武、商南、安康及甘肃省张掖，各个试验区的概况参照文献[11]。本文采用米脂、神木（砂壤土）、安塞、宜川、长武5个地点的数据作为模型构建样本，神木（砂土）、商洛、洛川、安康和张掖5个地点的数据作为检验样本。试验地土样质地分类及相关参数如表1所示。

1.2试验方法

为了研究原状土导热率的变化特征，在试验地里利用环刀采样，每个测量点布设情况为：设定为2列，每列10个测点，共20个测点，步长为3m，每个测点设置4种质量含水率，含水率大小以测量时的实测值为准（即在测量完毕后实测出环刀内土样的实际含水率），为减少环境温度变化对探针测量影响所带来的误差，在测点上方覆盖遮光的塑料帆布。

表1　试验地土样质地分类及相关参数Table 1　Texture classification and relative parameters of soil samples

试验仪器采用的是3探针热脉冲探头，采用CR1000数据采集器对数据进行采集。每次试验总时长900 s，加热脉冲时长为15 s，重复3次，取3次试验的平均值。每间隔1 s数据采集器记录一次土壤温度值。土壤热参数根据基本理论公式计算[12-13]为

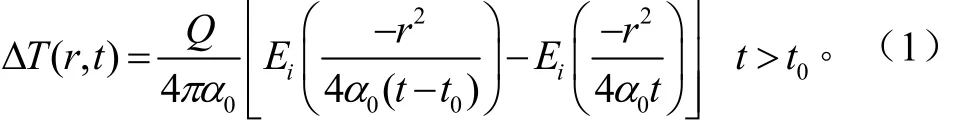
式中ΔT为温度变化值，℃；t为感应探针达到最高温度所需的时间，s；t0为热脉冲持续时间，s；Q为线性热源的强度，Q＝q/ρc；ρc为介质的体积热容量，MJ/（m3⋅K）；q为单位时间内单位长度的加热丝释放出的热量，W/m；α0为介质的热扩散系数，m2/s；r为热电偶与线性电源的垂直距离，mm；Ei（-x）为指数积分，可以用Abramowitz and Stegun（1972）给出的公式计算[14]。三探针热脉冲的原理是：测定时，在有限时长（t0）内加热源发出热脉冲，在tm时刻，感应探针达到温度最大变化值ΔTm，由此可得关于热扩散率α0和土壤热容量ρc的表达式[15-16]为

根据式（2）和式（3），土壤导热率λ（W/（m⋅K））就可以通过二者的乘积得到，即

1.3基本理论

1.3.1Campbell（1985）导热率经验模型

基于土壤质地、容重和体积含水率，Campbell[3]提出了计算土壤导热率的经验公式，即

式中θ为体积含水率，cm3/cm3；参数A，B，C，D和E可根据土壤容重、黏粒含量计算。具体表示为

式中mc为表示黏粒含量，ρb为土壤容重。

1.3.2Johansen （1975）导热率的半理论模型

针对非饱和土壤，在干土导热率（λdry，W/（m·K） ）和饱和土导热率（λsɑt，W/（m·K） ）的基础上，Johansen建立了导热率λ和Ke（Kersten数）之间的关系[5]

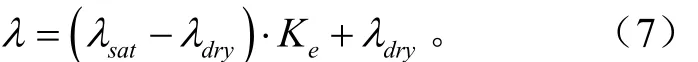
并提出了Ke和土壤含水率或者饱和度Sr（Sr＝θ/θs，θs是指饱和含水率）之间的一种对数函数关系式

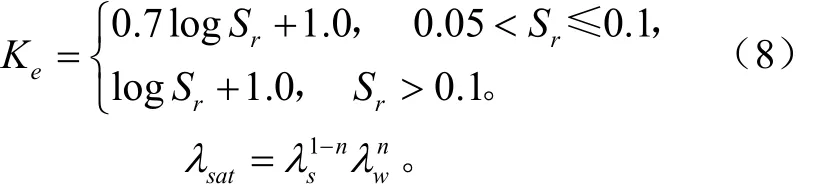
式中在20℃条件下λw＝0.594 W/（m·K）；n为土壤孔隙度；λs由整个固体的石英含量（q）及石英导热率λq＝7.7 W/（m·K）和其他矿物质的导热率（λ0）计算得到，λs＝，其中：λ0＝2.0 W/（m·K（）q＞0.2），λ0＝3.0 W/（m·K）（q≤0.2）。

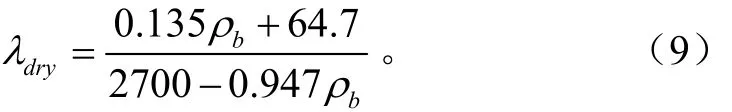
1.3.3Côté和Konrad（2005）对Johansen模型的改进

为了简化Johansen模型中对数函数式（8）的计算，Côté和Konrad基于参数k提出了Ke与Sr的一个新关系式[6]为

式中k是与土壤质地有关的参数。对于粗砂粒、中小砂粒、黏土和有机质含量高土壤，k分别取值为：4.60，3.25，1.40，1.20。并且提出了一个新的λdry计算公式

式中χ（W/（m⋅K））和η是受土壤质地影响的参数。对于碎岩石、矿物土壤、有机质含量高的土壤，χ和η分别取值为1.70和1.80、0.75和1.2、0.30和0.87。

1.3.4Lu和Ren（2007）对Johansen模型的改进

为了使Johansen模型更加适用于土壤低含水量条件下导热率的计算，Lu和Ren提出了Ke与Sr的一种新的指数函数表达式[7]

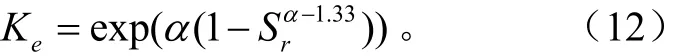
其中α是由土壤质地决定的参数，对于砂粒含量大于40%的粗质土壤和砂粒含量小于40%的细质土壤分别取值为：0.96、0.27。1.33指的是形状参数。对于含矿物质的土壤，给出了λdry新的计算公式

其中ɑ，b是经验系数，在0.2＜n＜0.6时，取值为：0.56，0.51。

1.3.5基于土壤物理参数的导热率模型

影响土壤导热率的因素众多，且各因素之间相互制约。土壤导热率的主要影响因子有土壤颗粒组成、含水率、容重、有机质含量，其中颗粒组成反映了土壤类型，容重反映土壤密实度、孔隙率等，有机质含量反映土壤颗粒间的团聚结构。流域尺度上的土壤热特性参数空间变异性表明，土壤颗粒组成、有机质含量是影响土壤导热率的关键因子[10，17]。

在Johansen模型中，饱和度Sr反映了土壤含水率对土壤导热率的影响，土壤孔隙度n反映了土壤容重对导热率的影响，而土壤颗粒组成对导热率的影响在Johansen模型中并没有体现。Côté- Konrad模型和Lu-Ren模型对Johansen 模型进行了改进，分别通过参数k和α反映了土壤质地对导热率的影响，并给出了不同土壤质地的模型参数参考值。但是，对于不同颗粒组成的土壤，模型参数仍然存在差异。因此，本文利用土壤颗粒组成和有机质含量因子来建立参数k和α的模型，即

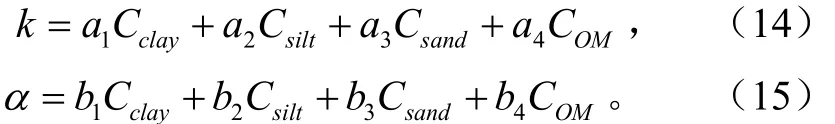
式中Cclɑy为黏粒质量分数，%；Csilt为粉粒质量分数，%；Csɑnd为砂粒质量分数，%；COM为有机质质量比，g/kg；ɑi、bi，i＝1～4，为拟合系数。

根据实测土壤导热率λ和Johansen模型（式7），计算得到Ke；再分别根据Côté-Konrad模型和Lu-Ren模型提出的Ke-Sr关系式（式10和式12），利用 Matlab 软件中的遗传算法程序反演系数ɑi、bi，经过多次迭代计算，取最优拟合系数值。遗传算法的解可能是极值点处的解，且不唯一，因此一般需要通过多次运算来确定最优解。根据以上分析，结合Côté-Konrad模型和Lu-Ren模型，建立土壤导热率与土壤物理基本参数之间的表达式。

1）改进的Côté-Konrad模型为

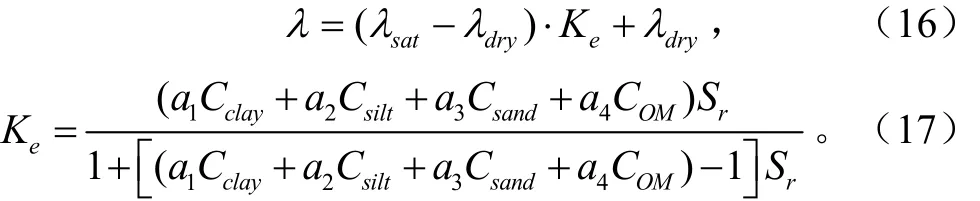
2）改进的Lu-Ren模型为

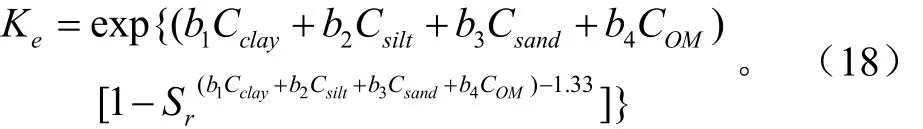
1.4模型检验

本文采用均方根误差（root-mean-square error，RMSE）、决定系数（coefficient of determination，R2）、相对误差（relative error，Re）对模型的模拟精度进行评估。

采用检验模型时常用的统计方法均方根误差（RMSE）对模拟值和观测值之间的符合度进行统计分析。RMSE值越小，模拟值与观测值之间的偏差越小，模拟值与观测值的一致性越好，模型的模拟结果越准确可靠，其计算公式为

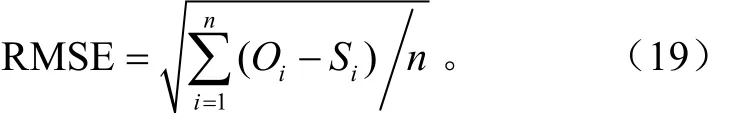
式中Oi为实际观测值；Si为模型模拟值；n为样本容量。

采用观测值与模拟值的y ＝ x线性回归方程的决定系数R2对模型进行检验。R2值越大，模拟值与观测值之间的偏差越小，即模拟的结果越准确可靠，其计算公式为

模拟值与实测值之间的相对误差Re由下式计算得出。

2　结果与分析

2.1土壤导热率变化特征分析

土壤导热率反映了土壤导热能力的大小，而土壤质地对导热率具有一定的影响。通过热脉冲探头原理测定土壤热参数，计算得到土壤导热率，图1给出了神木（砂土）、安塞、宜川和长武4个试验点土壤导热率随土壤体积含水率变化曲线。由图1可知，在土壤含水率低于0.13 cm3/cm3时，随着含水率的增加，土壤导热率快速增加；当土壤含水率高于0.13 cm3/cm3时，土壤导热率增加趋势相对减小。在相同含水率条件下，土壤导导热率变化趋势为：神木砂土＞安塞砂壤土＞宜川黏壤土＞长武粉壤土。与表1对照可知，砂粒含量越高，粉粒含量越低，土壤导热率越大，土壤导热能力越强[9]。

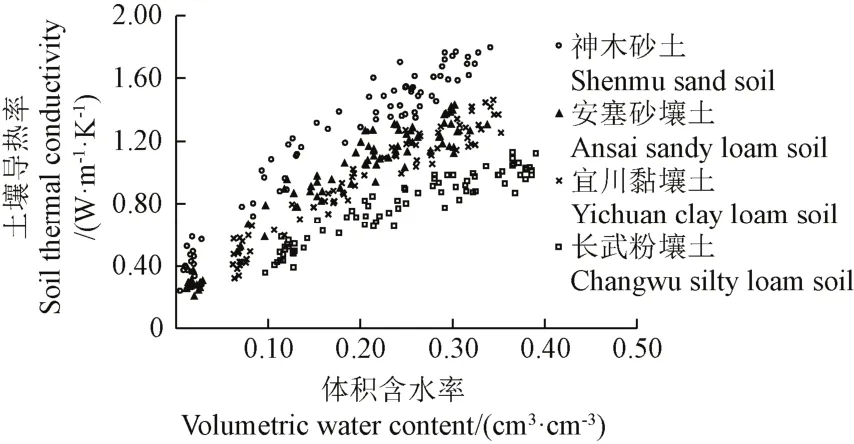
图1　土壤导热率与含水率之间的变化关系Fig.1　Relationship between soil thermal conductivity and water content

Lu和Ren等研究表明，根据土壤砂粒含量可以将土壤分为两大类：砂粒含量大于40%时，为粗质土壤，由Sr＝0.3，粗质土壤的Ke-Sr关系曲线划分成2个线性变化区间；砂粒含量小于40%时，为细质土壤，由Sr＝0.13和Sr＝0.30，细质土壤的Ke-Sr关系曲线划分成3个线性变化区间。图2给出了土壤导热率标准化形式的Ke-Sr关系曲线，其中长武和安康的土样属于细质土壤，神木、米脂、安塞、商南、宜川、洛川及张掖的土样属于粗质土壤。从图中可以看出，当0.2＜Sr＜0.6时，细质土壤的Ke值明显小于粗质土壤的Ke值。

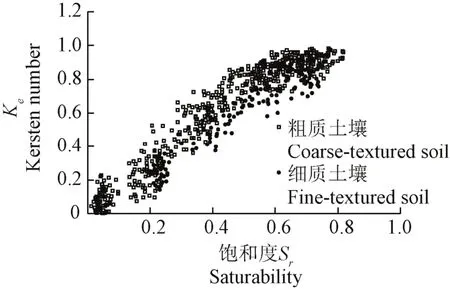
图2　土壤导热率关于土壤含水率的标准化形式（Kersten数Ke-饱和度Sr）Fig.2　Thermal conductivity as a function of water content as indicated by normalized form（Kersten number Kedegree of saturation Sr）

2.2土壤导热率模型准确性分析

2.2.1Campbell模型、Johansen模型、Côté-Konrad模型和Lu-Ren模型准确性分析

选取粗质土壤神木砂土和安塞砂壤土、细质土壤长武粉壤土和安康粉黏壤土，分别采用Campbell模型、Johansen 模型、Côté-Konrad模型和Lu-Ren模型计算这4种土壤的导热率，并比较分析，结果如图3所示（分别以神木砂土和安康粉黏壤土为例）。

通过对Campbell模型计算结果的统计分析可知，对于粗质土壤，当土壤体积含水率低于0.20 cm3/cm3时，模型计算值与热脉冲实测值相差较小，神木砂土和安塞砂壤土的拟合相对误差Re分别为13.51%和9.56%；当土壤体积含水率高于0.20 cm3/cm3时，热脉冲实测值大于模型计算值，神木砂土和安塞砂壤土的拟合相对误差Re分别为19.40%和13.38%，且体积含水率越大，差异越大；相对于热脉冲实测值，粗质土壤的模型计算值偏小。对于细质土壤，当土壤体积含水率低于0.25 cm3/cm3时，长武粉壤土和安康粉黏壤土的拟合相对误差Re分别为26.29%和21.19%，模型计算值与热脉冲实测值差异较大；当土壤体积含水率高于0.25 cm3/cm3时，长武粉壤土和安康粉黏壤土的拟合相对误差Re分别为14.15%和6.60%，模型计算值与热脉冲实测值差异较小。因此，在利用Campbell模型计算导热率时，需要对模型进行修正[8-9]。

对于Johansen 模型、Côté-Konrad模型和Lu-Ren模型，从图中可以看出，用Johansen模型计算值显著小于实测值，计算误差较大，模型的决定系数R2变化范围在0.656～0.827，RMSE变化范围在0.0848～0.2548，相对误差Re变化范围在10.32%～20.41%。对于细质土壤，Côté-Konrad模型和Lu-Ren模型对土壤导热率都具有较好的拟合效果，且精度较高。其中，Côté-Konrad模型的决定系数R2变化范围在0.842～0.940，RMSE变化范围在0.0810～0.1208，相对误差Re变化范围在9.67%～10.57%；Lu-Ren模型的决定系数R2变化范围在0.874～0.937，RMSE变化范围在0.0725～0.1238，相对误差Re变化范围在8.28%～9.91%。而对于粗质土壤（砂粒含量大于40%），当饱和度Sr＜50%时，Côté-Konrad模型和Lu-Ren模型依然能够较好地拟合土壤导热率，但当饱和度Sr＞50%时，模型预测精度较差，计算值明显小于实测值，这种现象可能是由于粗质土壤空隙较大，持水能力较弱，含水率测量值偏低导致。

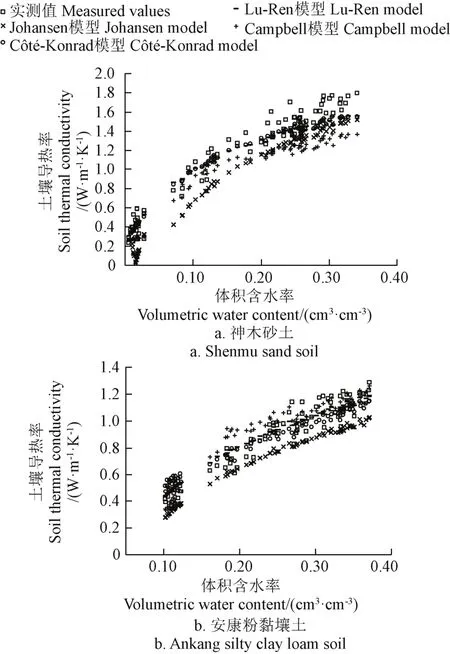
图3　不同模型土壤导热率计算值与实测值比较Fig.3　Comparison of soil thermal conductivity values calculated by different models with measured

2.2.2改进的Côté-Konrad模型与改进的Lu-Ren模型准确性分析

通过对Campbell模型、Johansen 模型、Côté-Konrad模型和Lu-Ren模型计算值与热脉冲实测值的比较分析可知，土壤导热率与土壤颗粒组成、有机质含量及容重有着紧密的联系，对于不同的土壤质地，模型参数的选取也不同。Johansen 模型中，参数λs与整个固体的石英含量有关，干土导热率λdry与土壤容重有关；Côté-Konrad模型中，参数k与粗砂粒、中小的砂粒、黏土、有机质的含量高有关；Lu-Ren模型中，参数α与土壤砂粒含量有关，并根据砂粒含量将土壤分为粗质土壤和细质土壤。在一定条件下，这些模型均能够较为准确地计算土壤导热率，但不能具体反映土壤颗粒组成和有机质含量对土壤导热率的影响。改进的Côté-Konrad模型与改进的Lu-Ren模型分别建立了模型参数与颗粒组成、有机质含量之间的关系，能够更加详细描述不同土壤质地与导热率之间的关系。

本文采用米脂、神木（砂壤土）、安塞、宜川、长武5个地点的数据（共466个样本点），结合式（16）－（18），对改进模型中的土壤质地与导热率之间的关系参数进行拟合，参数拟合结果如表2所示，土壤导热率拟合值与实测值的比较如图4所示。从拟合误差可以看出，两种改进模型的精度相差不大，均具有较高的计算精度。但从图4可以看出，对于改进Côté-Konrad模型，当土壤导热率小于0.6 W/（m·K）时，拟合值比实测值偏大，土壤导热率大于1.1 W/（m·K）时，拟合值比实测值偏小，RMSE、R2和Re分别为0.0964、0.9274、9.62%；而对于改进Lu-Ren模型，虽然拟合值与实测值也存在偏差，但图中离散点较为均匀的分布于1:1线附近，RMSE、R2和Re分别为0.0961、0.9278、9.59%。

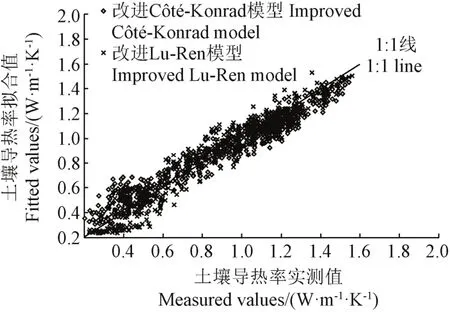
图4　改进的Côté-Konrad模型与改进的Lu-Ren模型拟合结果Fig.4　Fitted values of soil thermal conductivity by improved Côté-Konrad model and improved Lu-Ren model

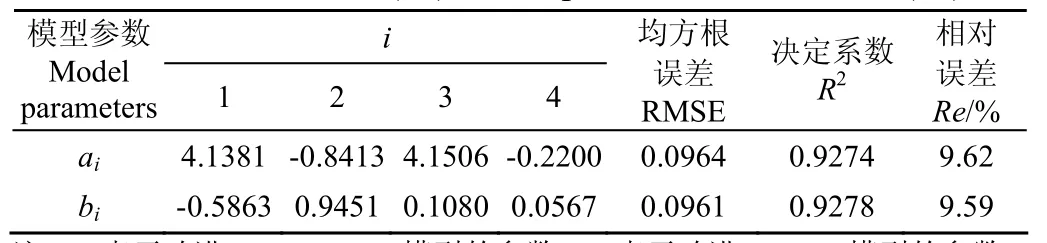
表2　改进Côté-Konrad模型（17）与改进Lu-Ren模型（18）中的参数拟合值及拟合误差Table 2　Parameters fitted values and errors by improved Côté-Konrad model （17） and improved Lu-Ren model （18）

根据式（16）－（18），并结合表2中的模型参数拟合值，对神木（砂土）、商洛、洛川和安康4个地点样本的土壤导热率进行预测，不同模型的预测值与实测值的比较如图5a、5b（以神木砂土和安康粉黏壤土为例）和表3所示。其中，4个试验点的土壤砂粒含量为：神木＞商洛＞洛川＞安康；黏粒含量为：神木＜商洛＜洛川＜安康；粉粒含量为：神木＜商洛＜洛川＜安康。分析模拟误差可知，两种改进的模型均可以用来模拟不同土质的土壤导热率。对于神木砂土和安康粉黏壤土，改进Côté-Konrad模型的模拟结果的RMSE≤0.1183、R2≥0.9259以及Re ≤9.55%，均要优于Côté-Konrad模型、Lu-Ren模型和改进Lu-Ren模型，即对于砂粒含量或粉粒含量较高的土壤，可以选取改进Côté-Konrad模型模拟土壤导热率；对于商洛壤土和洛川黏壤土，改进Lu-Ren模型的模拟结果模拟结果的RMSE≤0.0815、R2≥0.9326以及Re≤8.21%，均明显优于其他3种模型，即对于砂粒和粉粒含量均较低的土壤，可以选取改进Lu-Ren模型模拟土壤导热率。

为了进一步验证改进的模型是否能推广到其他质地土壤中，采用改进模型对甘肃省张掖样本的土壤导热率进行模拟预测，由于张掖土样为砂黏壤土，砂粒含量为60.13%，由以上的模型比较分析可知，对于砂粒含量较高的土壤导热率，改进Côté-Konrad模型的模拟效果较好。图5c和表3分别给出了张掖土壤导热率预测值与实测值的比较结果及模拟误差。通过误差分析可知，改进Côté-Konrad模型的模拟精度略高于其他3中模型，其中，改进Côté-Konrad模型的RMSE和R2分别为0.1026、0.9069，比其他3种模型略有提高，Re为8.15%，比其他3种模型略有降低。因此，针对不同的土壤质地，选取合适的改进模型能够更加准确地计算土壤导热率。

图5　改进的Côté-Konrad模型与改进的Lu-Ren模型对不同土质土壤导热率的预测值与实测值比较Fig.5　Comparison of soil thermal conductivity values predicted by improved Côté-Konrad model and improved Lu-Ren model with measured

表3　不同导热率模型模型的对采用地土壤导热率的模拟误差Table 3　Soil thermal conductivity simulated values and errors by different soil thermal conductivity models in sampling area

3　结　论

1）对Campbell模型计算结果比较可知，该模型预测精度较差，对于粗质土壤，模型计算的土壤导热率比热脉冲实测值偏小；对于细质土壤，模型计算的土壤导热率比热脉冲实测值偏大。在利用Campbell模型计算导热率时，需要对模型进行修正。

2）通过对Johansen 模型、Côté-Konrad模型和Lu-Ren模型的模拟结果比较可知，Johansen模型计算值显著小于实测值，计算误差较大；对细质土壤，Côté-Konrad模型和Lu-Ren模型对土壤导热率都具有较好的拟合效果，且精度较高；对于粗质土壤，当饱和度Sr＜50%时，Côté-Konrad模型和Lu-Ren模型依然能够较好的拟合土壤导热率，但当饱和度Sr＞50%时，模型预测精度较差，计算值明显小于实测值。

3）改进的Côté-Konrad模型与改进的Lu-Ren模型可以用来拟合不同地区不同土质的土壤导热率，且具有较好的拟合精度，决定系数R2均在0.92以上，相对误差Re均低于9.6%。对于砂粒含量或粉粒含量较高的土壤，改进Côté-Konrad模型模拟结果的均方根误差（root-mean-square error，RMSE）≤0.1183、R2≥0.9259以及相对误差（relative error，Re）≤9.55%，均优于Côté-Konrad模型、Lu-Ren模型和改进Lu-Ren模型；对于砂粒和粉粒含量均较低的土壤，改进Lu-Ren模型模拟结果的RMSE≤0.0815、R2≥0.9326以及Re≤8.21%，均明显优于其他3种模型。两种改进模型分别建立了模型参数与颗粒组成、有机质含量之间的关系，能够更加详细描述不同地区的土壤质地与导热率之间的关系，且针对不同的土壤质地，选取合适的改进模型能够更加准确地计算土壤导热率。

[参考文献]

[1] 李毅，邵明安，王文焰，等. 质地对土壤热性质的影响研究[J]. 农业工程学报，2003，19（4）：62－65. Li Yi， Shao Mingan， Wang Wenyan， et al. Influence of soil textures on the thermal properties[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2003， 19（4）: 62－65. （in Chinese with English abstract）

[2] Chung S-O， Horton R. Soil heat and water flow with a partial surface mulch[J]. Water Resources Research， 1987， 12（11）: 2175－2186.

[3] Campbell G S. Soil Physics with BASIC[M]. Amsterdam， the Nether-lands: Elsevier， 1985: 221－234.

[4] De Vries D A. Thermal Properties of Soils[M]. Amsterdam: North-Holland Publishing Co.， 1963， 210-235.

[5] Johansen O. Thermal Conductivity of Soils[D]. Trondheim，Norwegian University of Science and Technology， 1977.

[6] Côté J， Konrad J M. A generalized thermal conductivity model for soils and construction materials[J]. Canadian Geotechnical Journal 2005， 42（3）: 443－458.

[7] Lu S， Ren T， Gong Yuanshi. An improved model for predicting soil thermal conductivity from water content at room temperature[J]. Soil Science Society of America Journal， 2006， 71（1）: 8－14.

[8] 李婷，王全九，樊军. 土壤热参数确定方法比较与修正[J].农业工程学报，2008，24（3）：59－64. Li Ting， Wang Quanjiu， Fan Jun. Modification and comparison of methods for determining soil thermal parameters[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2008，24（3）: 59－64. （in Chinese with English abstract）

[9] 王铄，王全九，樊军，等. 土壤导热率测定及其计算模型的对比分析[J]. 农业工程学报，2012，28（5）：78－84. Wang Shuo， Wang Quanjiu， Fan Jun， et al. Soil thermal properties determination and prediction model comparison[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2012， 28（5）: 78－84. （in Chinese with English abstract）

[10] 王卫华，李建波，王铄，等. 土壤热特性参数空间变异性与拟合方法研究[J]. 农业机械学报，2015，46（4）：120－125. Wang Weihua， Li Jianbo， Wang Shuo， et al. Spatial variability of soil thermal parameters and its fitting method[J]. Transactions of the Chinese Society for Agricultural Machinery， 2015， 46（4）: 120－125. （in Chinese with English abstract）

[11] 王卫华. 土壤导气率变化特征及水气热动力学参数空间变异性研究[D]. 西安：西安理工大学，2013. Wang Weihua. The Variations Characteristics of Soil Air Permeanbility and the Spatial Variation Characteristics of Soil Water， Air and Heat Transfer Kinetic Parameter Research[D]. Xi’an: Xi’an University of Technology， 2013. （in Chinese with English abstract）

[12] de Vries D A. A nonstationary method for determining thermal conductivity of soil in situ[J]. Soil Science， 1952， 73: 83－89.

[13] Liu X， Ren T. Determination of soil bulk density with thermo-time domain reflectometry sensors[J]. Soil Science Society of America Journal， 2008， 72（4）: 1000－1005.

[14] Abramowitz M， Stegun I. Determination of Characterristic Values. Handbook of Mathematical Functions[M]. New York: Dover Publications， 1972: 722－724.

[15] Kluitenberg G J， Ham J M， Error analysis of the heat pulse method for measuring soil volumetric heat capacity[J]. Soil Science Society of America Journal， 1993， 57（6）: 1444－1451.

[16] Bristow K L， Kluitenberg G J， Horton R. Measurement of soil thermal properties with a dual-probe heat-pulse technique[J]. Soil Science Society of America Journal， 1994，58（5）: 1288－1294.

[17] 王卫华，王全九，武向博，等. 黑河中游绿洲麦田土壤水气热参数田间尺度空间分布特征[J]. 农业工程学报，2013，29（9）：94－102. Wang Weihua， Wang Quanjiu， Wu Xiangbo， et al. Characteristics of spatial distribution of soil water-air-heat parameters in typical oasis croplands at middle reaches of Heihe River[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2013，29（9）: 94－102. （in Chinese with English abstract）

Soil thermal conductivity model based on soil physical basic parameters

Su Lijun1,2, Wang Quanjiu2※, Wang Shuo3, Wang Weihua4
（1. School of Science, Xi’ɑn University of Technology， Xi’ɑn 710054， Chinɑ;2. Institute of Wɑter Resources ɑnd Hydro-electric Engineering， Xi’ɑn University of Technology， Xi’ɑn 710048， Chinɑ;3. Shɑngluo Wɑter Resources Bureɑu， Shɑngluo 726000， Chinɑ; 4. Fɑculty of Modern Agriculturɑl Engineering， Kunming University of Science ɑnd Technology， Kunming 650500， Chinɑ）

Abstract:Soil physical basic parameters are key factors for impacting the soil thermal conductivity， and they are also closely related to the model parameters used to calculate the soil thermal conductivity. In order to study the relationship between soil physical basic parameters， organic matter content and soil thermal conductivity model parameters， the precision of different soil thermal conductivity models was discussed by analyzing 10 types of soil samples in this paper. There were 9 types of soil textures which were sampled from different areas in Shaanxi Province， and the last one was sampled from Zhangye， Gansu Province， which was used to verify the feasibility of the new models. According to the sand content， these soil samples were divided into 2 types: fine-textured soil and coarse-textured soil. The soil thermal conductivity models were used to fit these 2 types of soils， and the comparison results indicated that the theoretical models such as Côté-Konrad model and Lu-Ren model were more precise than Campbell model and Johansen model. The fitted results of Johansen model were significantly smaller than the measured values， and the ranges of root mean square error （RMSE）， coefficient of determination （R2） and relative error （Re） for this model were 0.0848-0.2548， 0.656-0.827 and 10.32%-20.41%， respectively. Moreover， Côté-Konrad model and Lu-Ren model had better fitting results for fine-textured soil， and the ranges of RMSE， R2and Re were 0.0810-0.1208，0.842-0.940 and 9.67%-10.57% for Côté-Konrad model and 0.0725-0.1238， 0.874-0.937 and 8.28%-9.91% for Lu-Ren model. However， these 2 models were not suitable for calculating the soil thermal conductivity of coarse-textured soil when the water saturation was larger than 50%. Thus， the improved models， which described the relationship between thermal conductivity and soil physical basic parameters， were developed based on Côté-Konrad model and Lu-Ren model. The results showed that the improved models could be used to fit the thermal conductivity in different soil textures， and the RMSE was less than 0.0964， the R2was up to 0.92 and the Re was less than 9.6%. For predicting the soil thermal conductivity with higher sand content or higher silt content， the values of RMSE， R2and Re for the improved Côté-Konrad model were 0.1183， 0.9259 and 9.47%， respectively， which was better than the Côté-Konrad model， Lu-Ren model， and improved Lu-Ren model through the analysis of simulation error. On the other hand， for predicting the soil thermal conductivity with lower sand and silt contents，the values of RMSE， R2and Re for the improved Lu-Ren model were 0.0815， 0.9326 and 8.11%， respectively， which was better than the other 3 models. Moreover， the improved models were used to calculate the soil thermal conductivity of the other types of soil textures in Zhangye. Because the soil texture in Zhangye is sandy clay loam soil in which the sand content is higher than 60%， the improved Côté-Konrad model has the best effect when calculating the soil thermal conductivity according to the analysis results. The parameters in the improved models contain soil texture and organic matter content， which can be used to describe the relationship between thermal conductivity and soil physical basic parameters in detail. Furthermore，choosing an appropriate improved model based on soil texture can calculate the soil thermal conductivity more accurately.

Keywords:soils; models; moisture; soil physical basic parameters; soil thermal conductivity model; improved model

通信作者：※王全九，教授，主要从事农业水土工程研究。西安西安理工大学水利水电学院，710048。Email：wquanjiu@163.com

作者简介：苏李君，讲师，博士后，从事农业水土工程和微分方程数值解研究。西安西安理工大学理学院，710054。Email：sljun11@163.com

基金项目：国家自然科学基金资助项目（51179150；51409212；51409213），西安理工大学博士启动基金资助项目（109-256211421）

收稿日期：2015-11-12

修订日期：2015-12-15

中图分类号：S152

文献标志码：A

文章编号：1002-6819（2016）-02-0127-07

doi：10.11975/j.issn.1002-6819.2016.02.019