采用Kriging模型的离心压缩机叶轮多目标参数优化

左曙光，韦开君，吴旭东，聂玉洁，许思传（同济大学新能源汽车工程中心，上海 201804）



采用Kriging模型的离心压缩机叶轮多目标参数优化

左曙光，韦开君，吴旭东※，聂玉洁，许思传
（同济大学新能源汽车工程中心，上海 201804）

摘要：为进一步探索高性能、低噪声的离心压缩机优化设计方法，该文选用某燃料电池车用小型高转速离心压缩机为研究对象，通过三维内流场非定常分析对其气动性能和气动噪声进行计算，仿真求得的压升曲线与试验基本一致。基于该数值模型，采用最优拉丁方试验设计分析了叶片进口角、叶片出口角、尾缘倾角、叶顶间隙和叶片厚度对压缩比、等熵效率和整机声功率级的影响，结果表明叶片厚度和叶顶间隙最为关键，与压缩比和等熵效率负相关，与声功率级正相关，前倾叶片较后倾叶片噪声更低。采用Kriging模型对数值计算结果进行拟合，利用多目标遗传算法对Kriging模型进行循环优化设计。优化结果表明，Kriging模型精度满足需求，优化方案在设计工况点的压缩比提高3.56%，等熵效率提高1.02%，整机声功率级下降3.79 dB，在非设计工况点的压缩比和等熵效率也有提高，综合性能得到明显改善。该研究可为高性能、低噪声离心压缩机的优化设计提供参考。

关键词：模型；优化；叶轮；离心压缩机；非定常分析；气动噪声；Kriging模型

左曙光，韦开君，吴旭东，聂玉洁，许思传. 采用Kriging模型的离心压缩机叶轮多目标参数优化[J]. 农业工程学报，2016，32（2）：77－83.doi：10.11975/j.issn.1002-6819.2016.02.012http://www.tcsae.org

Zuo Shuguang， Wei Kaijun， Wu Xudong， Nie Yujie， Xu Sichuan. Multi-objective parameter optimization of centrifugal compressor impeller with Kriging model[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2016， 32（2）: 77－83. （in Chinese with English abstract）doi：10.11975/j.issn.1002-6819.2016.02.012 http://www.tcsae.org

Email：sgzuo@tongji.edu.cn

Email：wuxudong@tongji.edu.cn

0　引　言

随着燃料电池汽车产业化的推进，其振动噪声性能越来越受到重视。与传统汽车不同，燃料电池汽车的噪声源主要来自空辅系统，尤其是空压机产生的气动噪声[1]。离心压缩机由于其结构紧凑、压缩比高的优点，在车用中高压燃料电池空辅系统中得到广泛应用，但高工作转速（通常在60 000～100 000 r/min）随之产生很大的噪声。由于流场的仿真计算耗时，离心压缩机的传统优化设计很难基于全局优化算法直接对压缩机多个结构参数进行多目标的迭代寻优。尤其是气动噪声的优化设计，通常局限在对个别结构参数的改进，例如蜗舌形状、蜗壳结构或采用被动降噪措施。这些措施虽然可以取得一定的降噪效果，但也容易导致压缩机气动性能不同程度的下降[2-4]。

随着近似模型技术的发展，将近似模型技术引入叶轮机械优化设计，用快速响应的近似模型代替流场仿真的数值模型进行全局寻优，可以在设计初期实现对叶轮机械的多目标优化[5]。国内外基于近似模型的叶轮机械优化设计大多集中在压缩比/扬程和效率这些气动/水力性能参数优化，常采用一阶或二阶响应面模型[6]、径向基函数[7]、Kriging模型[8-10]等作为近似模型，采用遗传算法[11-12]、蚁群算法[13]、神经网络[14]等方法进行多参数多目标全局寻优。随着气动噪声数值方法和计算资源的进步，结合近似模型的叶轮机械气动噪声优化设计成为可能。但是此类研究多集中在轴流风机[15-17]或离心通风机[18-19]，对噪声的预测通常基于定常计算得到的涡量和压力分布，准确度不足。

针对以上问题，本文提出了一种基于Kriging近似模型的离心压缩机多目标优化设计方法，研究了离心压缩机叶片进口角、叶片出口角、尾缘倾角、叶顶间隙、叶片厚度与压缩比、等熵效率和整机声功率级之间的关系，并基于数值计算结果分析了优化后叶轮性能改善的原因。

1　数值计算方法

1.1流场计算方法

本文研究的离心压缩机由叶轮、无叶扩压器和蜗壳组成，叶轮共有8个主叶片和8个分流叶片，压缩机进口直径Ds1＝38 mm，叶轮外径D1＝70 mm，叶片高度b＝4 mm，扩压器外径D2＝110 mm，设计工况点的质量流量Q＝0.08 kg/s，压缩比πc＝1.65，转速n＝80 000 r/min。离心压缩机结构如图1所示。

为了稳定流场并加快计算收敛，将进出口段分别延长。计算域分为进口段、叶片旋转区域、蜗壳区域和出口段，其中蜗壳区域采用混合网格，蜗舌处采用四面体非结构网格，其他区域全部采用六面体结构网格。为保证CFD网格的声学求解精度，需保证分析的最小波长内至少布置20个网格，拟定最高分析频率为15 kHz，则最大网格不超过1.2 mm，网格总数约107万。

图1　离心压缩机结构示意图Fig.1　Schematic diagram of centrifugal compressor

流场计算采用商业软件Fluent，非定常计算的湍流模型采用RNG k-ε模型，取标准壁面函数，压力-速度耦合采用SIMPLE方法，对流项采用二阶迎风格式，扩散项采用二阶中心格式，时间项采用二阶隐式格式，进出口采用压力边界条件。离心压缩机工作转速为80 000 r/min，取每个旋转周期内时间步数为40步，非定常计算时间步长Δt 为1.875×10-5s，流场稳定后共计算2 048步。则计算得到的最大分析频率fm为26 667 Hz，频率分辨率Δf 为26 Hz。

yplus是用来表征近壁面湍流的无量纲参数，根据yplus的大小可将湍流边界层分为几部分：1）0＜yplus≤5，流体处于黏性层；2）5＜yplus≤20，流体处于缓冲层；3）20＜yplus≤200，流体处于对数律层；4）yplus＞200，流体处于外边界层。不同的边界层有不同的流体特点，采用标准壁面函数进行数值仿真时，要求边界层网格分布在完全湍流区域，即对数律区域[20]。图2为仿真得到的压缩机壁面yplus分布，由图2可知，压缩机壁面的yplus在30～200之间，满足数值模型需求。

图2　压缩机壁面yplus分布云图Fig.2　yplus contours of compressor wall

压缩比πc和等熵效率ηɑd是衡量压缩机气动性能的主要参数，计算方法可由式（1）与式（2）确定。

式中πc为离心压缩机的压缩比；ηɑd为等熵效率；pti、pto分别为压缩机进、出口总压，Pa；Tti、Tto分别为压缩机进、出口总温，K。由于在不同时刻压缩机的进出口总压、总温不同，为便于比较，这里pti、pto、Tti、Tto为2 048个非定常计算时间步的平均值。

1.2气动噪声计算方法

由三维非定常流场计算得到的声源信息，采用FW-H方法计算离心压缩机气动噪声，包括由表面速度变化引起的声源，即单极子声源；由表面脉动压力引起的声源，即偶极子声源；由瞬时应力施加于流体上引起的声源，即四极子声源[21]。偶极子声源在离心压缩机气动噪声中起主导作用[22]，因此在Fluent仿真中选取蜗壳壁面固定偶极子源和叶片壁面运动偶极子源作为声源，计算离心压缩机辐射声场。根据GB/T2888-2008《风机和罗茨鼓风机噪声测量方法》布置噪声监测点，整机声功率级为

式中LWA为整机声功率级，dB（A）；S为传递面积，m2；S0为标准面积，m2；为平均声压级，dB（A）；L1，L2，…，Ln分别为不同噪声测点测得的声压级，dB（A）；n为噪声测点数量。

1.3数值模型验证

为验证数值模型的准确性，对离心压缩机进行性能试验，试验现场布置如图3所示。压缩机噪声测试采用G.R.A.S. 40PH 1/2” 传声器，试验数据采集及分析采用LMS Test.Lab 系统。

图3　试验现场布置Fig.3　Experimental setup

由于条件限制，试验中离心压缩机驱动电机所能达到的最高转速为50 000 r/min。调节压缩机出口管阀门开度，分别测试40 000、50 000 r/min 2个稳态转速下，大、中、小流量3个工况下压缩机出口压力。基于前文所述数值模型分别计算转速为40 000、50 000 r/min压缩机的压力-流量曲线，将数值计算结果与试验结果对比，如图4所示。由图4可知，数值计算结果略高于试验结果，这是由于计算中没有考虑机壳壁面粗糙度等影响。总体上数值计算结果与试验结果基本一致，该数值模型可用于进一步的计算与分析。

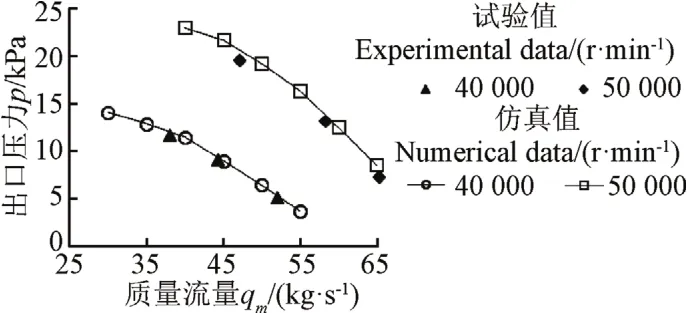
图4　数值仿真与试验压力-流量曲线对比Fig.4　Comparison of pressure ratio between numerical and experimental data

2　多目标优化设计

2.1Kriging模型

采用进化算法的多目标优化设计通常需要进行大量的搜索计算，如果直接采用数值计算模型，将耗费巨大的计算资源与时间成本。Kriging模型作为一种无偏插值函数模型，在气动设计领域获得了广泛应用[5]。Kriging模型可表示为以下形式

式中x为设计变量，y（x）为待拟合的响应函数，f（x）为已知的回归模型，通常是多项式函数，β为相应的待定参数，f（x）Tβ是一个确定性过程，相当于对全部设计空间的全局模拟；Z（x）是均值为0、方差为σ2的随机过程，表示对全局模拟的偏差。模型详细构建过程详见文献[23]。

采用最优拉丁方设计方法，建立了不同叶片进口角β1、叶片出口角β2、尾缘倾角γ、叶顶间隙e、叶片厚度t的5因素21水平包括21次试验的初始样本集，通过数值计算得到相应的响应值，各设计变量对响应的影响程度如图5所示。由图5可知，对响应值影响最大的2个参数是叶片厚度和叶顶间隙，当叶片厚度和叶顶间隙增加时，压缩比、等熵效率降低，声功率级上升。各参数间存在一定交互作用。

图5　设计变量对响应的影响程度Fig.5　Influences of design parameters on responses

基于数值计算结果，拟合叶片进口角、叶片出口角、尾缘倾角、叶顶间隙、叶片厚度关于压缩比、效率、声功率的Kriging模型。对拟合Kriging模型进行误差分析，结果如表1所示。由表1可知，Kriging模型各项误差指标均小于工程设计领域中常用的许用值[24]。本文模型决定系数R2均大于0.9，说明Kriging模型的精度满足要求，可以作为多目标优化的代理模型。

表1　Kriging模型误差分析Table 1　Error analysis of Kriging model

2.2多目标优化

选取离心压缩机压缩比πc、等熵效率ηɑd、整机声功率LWA为优化目标，叶片进口角β1、叶片出口角β2、尾缘倾角γ、叶顶间隙e、叶片厚度t为优化变量，优化问题可描述为

式中πc为离心压缩机的压缩比；ηɑd为等熵效率；β1为叶片进口角，（°）；β2为叶片出口角，（°）；γ为叶片尾缘倾角，（°）；e为叶顶间隙，mm；t为叶片厚度，mm。

基于Kriging模型，采用多目标遗传算法NSGA-Ⅱ[25]进行优化设计，设定初始种群数为200，遗传代数为1 000，交叉概率为0.9，变异概率为0.2。为进一步提高Kriging代理模型的精度，对模型得到的最优点进行精确数值计算，利用该精确计算的数据更新原模型，进一步提高最优区间附近的代理模型精度，进一步提高最优区间附近的代理模型精度，直至得到更理想的优化结果。离心压缩机多目标优化设计流程如图6所示。

3　优化结果与分析

3.1叶片结构对比

优化得到的Pareto解集如图7所示，由图7可知，声功率级和压缩比2个目标无法同时满足最优，Pareto前沿的斜率逐渐减小，当压缩比较低时，随压缩比上升声功率级几乎不增加；当压缩比较高时，压缩比的小幅上升也会造成声功率级的大幅增加。声功率级和等熵效率的Pareto前沿与此类似。本文更关注离心压缩机的噪声特性，最终选取优化设计点如图7所示。

图6　离心压缩机多目标优化设计流程图Fig.6　Flowchart of multi-objective optimization design of centrifugal compressor

图7　Pareto最优解集Fig.7　Pareto diagram of optimized results

优化前后离心压缩机结构参数对比如表2所示。

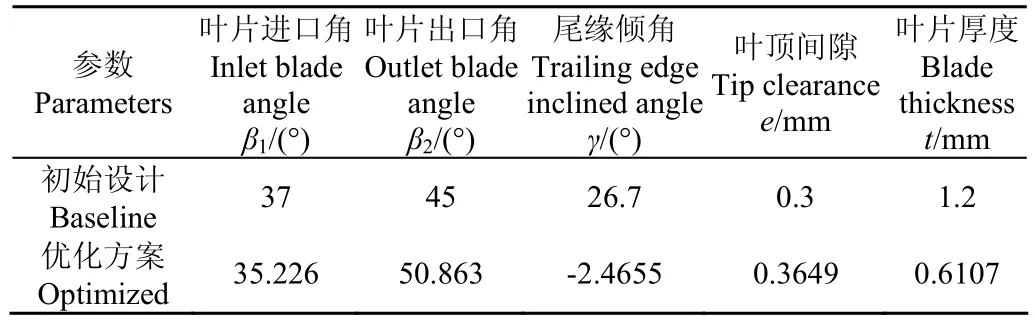
表2　优化前后结构参数对比Table 2　Parameters of baseline and optimized designs

图8对比了优化前后叶片的型线，由图8可知，优化后叶片厚度变薄，出口由后倾变为前倾，叶片整体扭曲程度降低，流道曲率变化也更为平滑。通常前倾叶片气动负荷分布比较均匀，因而具有较高的效率和较宽的工作流量区间。由前文各设计变量对优化目标的影响因素分析可知，当叶片厚度和叶顶间隙增加时，压缩比、等熵效率降低，声功率级上升。优化结果较初始设计，叶顶间隙增大了21.6%，叶片厚度减小了49.1%，压缩比和等熵效率的提高主要来源于叶片厚度的减小。但值得注意的是，优化后尾缘倾角减小了109.2%，由后倾变为前倾。由图5可知，尾缘倾角γ与声功率级呈正相关，对压缩比和效率的影响较小。因此，尾缘倾角的大幅减小是优化后声功率级降低的主要原因。同时，考虑到实际制造成本，叶顶间隙不能过小，在满足性能和噪声需求的基础上可选择稍大的叶顶间隙，故本文在Pareto解集中挑选该点作为最终优化结果。

图8　优化前后叶片型线对比Fig.8　Comparison of blade profiles before and after optimization

3.2气动性能及噪声对比

为校核优化结果，利用优化前后的叶轮，结果原有扩压器和蜗壳，在设计转速下进行了多个工况点的定常计算，图9所示为优化前后离心压缩机性能曲线的对比。由图9可知，与优化前相比，优化后设计工况和非设计工况的压缩比和等熵效率均有一定提高。

图9　优化前后离心压缩机性能曲线对比Fig.9　Performance maps before and after optimization

对优化设计点进行非定常计算，与初始设计对比结果如表3所示。由表3可知，采用Kriging模型与数值计算所得的压缩比、等熵效率和声功率的误差均小于0.5%，Kriging模型具有很高的预测精度。优化方案较初始设计压缩比提高了3.56%，等熵效率提高了1.02%，整机声功率级下降了3.79 dB，综合性能得到明显改善。

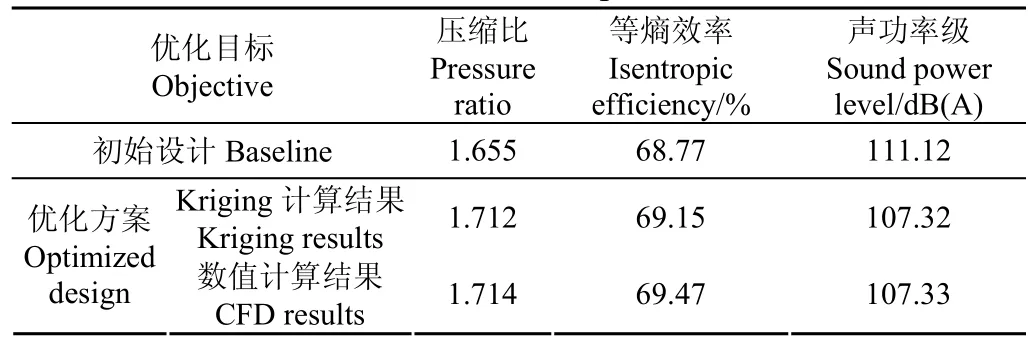
表3　优化结果对比Table 3　Results of optimization

为进一步分析优化结果，对优化前后离心压缩机内部流动进行分析。图10所示为压缩机横截面的压力云图，由图10可知，优化后压缩机压力显著提高，扩压器和蜗壳内压力变化更加平缓，蜗舌处由于泄漏引起的压力损失更小。

图10　压缩机横截面压力云图对比Fig.10　Pressure contours of compressor cross section

图11所示为叶轮出口处马赫数分布对比，由图11可知，优化前，叶片通道内低速区域堆积在叶片吸力面上部，并在主叶片根部形成回流。优化后叶轮出口处速度整体上进一步降低，局部堆积和回流现象减弱，叶片通道内和根尖速度分布均匀性变好。这种改变使得下游扩压器流场中高低能流体的掺混和损失更少，这也是优化后压缩机的性能得到改善的原因。

图11　叶轮出口马赫数对比Fig.11　Mach number at impeller outlet

图12所示为80%叶高处叶片间流面的熵云图和面流线图。由图12可知，优化前在分流叶片中后部存在高熵区，从面流线可以看出，优化前分流叶片中后部的高熵区是由横向涡流引发的流动损失导致。优化后叶片流道内横向涡流明显减弱，整体熵增明显降低。

图12　80%叶高处叶片间流面的熵云图和面流线对比Fig.12　Entropy contours and streamlines at 80% span of blade-to-blade surface

在实际运行中，离心压缩机出口通过管道经加湿器进入燃料电池电堆，大部分气动噪声由进口直接向外辐射[26]。对优化前后离心压缩机进口处噪声进行分析，如图13所示。由图13可知，优化后叶片通过频率处噪声降低了16 dB，旋转基频及其谐频处的离散噪声均有下降，全频带内宽频噪声也有所下降，尤其是0～1 800 Hz 和10 000～16 000 Hz频段。优化方案整体降噪效果显著。

图13　优化前后离心压缩机噪声对比Fig.13　Sound pressure level spectrums before and after optimization

4　结　论

1）叶片厚度和叶顶间隙是2个最关键参数，当叶片厚度和叶顶间隙增加时，压缩比、等熵效率降低，声功率级上升。减小尾缘倾角可改善叶片出口流动，前倾叶片较后倾叶片噪声更低。各设计参数间存在一定交互作用。

2）优化方案在设计工况点较初始设计压缩比提高了3.56%，等熵效率提高了1.02%，原因为优化后叶片出口速度分布更加均匀，叶片间横向涡流损失减少。非设计工况点的压缩比和等熵效率均有提高。

3）优化后设计工况点的整机声功率级下降3.79 dB，叶片通过频率处噪声降低16 dB，旋转频率及其谐频处离散噪声以及0～1 800 Hz、10 000～16 000 Hz频段内宽频噪声均有下降。

本文将最优拉丁方设计、Kriging模型、多目标遗传算法、循环优化相结合，提出的优化方法可以为高性能、低噪声燃料电池车用离心压缩机优化设计提供参考，并可以推广到其他叶轮机械的优化设计中。

[参考文献]

[1] 郭荣，万钢，左曙光，等. 燃料电池轿车主要噪声源识别的试验研究[J]. 汽车工程，2007，29（5）：377－380. Guo Rong， Wan Gang， Zuo Shuguang， et al. An experimental study on noise sources identification for fuel cell vehicle[J]. Automotive Engineering， 2007， 29（5）: 377－380. （in Chinese with English abstract）

[2] 刘晓良，袁民建，毛义军，等. 前向离心风机蜗壳出口结构的数值优化[J]. 西安交通大学学报，2009，43（5）：61－65. Liu Xiaoliang， Yuan Minjian， Mao Yijun， et al. Numerical optimization of volute outlet structure for forward-curved centrifugal fan[J]. Journal of Xi'an Jiaotong University， 2009，43（5）: 61－65. （in Chinese with English abstract）

[3] 顾媛媛，袁民建，毛义军，等. 离心风机吸声蜗壳结构的数学物理模型及实验验证[J]. 西安交通大学学报，2011，45（1）：83－88. Gu Yuanyuan， Yuan Minjian， Mao Yijun， et al. Mathematical- physical model of noise-absorbing volute of centrifugal fan and experimental validation[J]. Journal of Xi’an Jiaotong University， 2011， 45（1）: 83－88. （in Chinese with English abstract）

[4] Gu Yuanyuan， Qi Datong， Mao Yijun， et al. Theoretical and experimental studies on the noise control of centrifugal fans combining absorbing liner and inclined tongue[J]. Proceedings of the Institution of Mechanical Engineers， Part A: Journal of Power and Energy， 2011， 225（6）: 789－801.

[5] 席光，王志恒，王尚锦. 叶轮机械气动优化设计中的近似模型方法及其应用[J]. 西安交通大学学报，2007，41（2）：125－135. Xi Guang， Wang Zhiheng， Wang Shangjin. Aerodynamic optimization design of turbomachinery with approximation model method[J]. Journal of Xi'an Jiaotong University， 2007，41（2）: 125－135. （in Chinese with English abstract）

[6] Guo Shuai， Duan Fei， Tang Hui， et al. Multi-objective optimization for centrifugal compressor of mini turbojet engine[J]. Aerospace Science and Technology， 2014， 39（1）: 414－425.

[7] Khalfallah S， Ghenaiet A， Benini E， et al. Surrogate-based shape optimization of stall margin and efficiency of a centrifugal compressor[J]. Journal of Propulsion and Power，2015， 31（6）: 1－14.

[8] Olivero M， Pasquale D， Ghidoni A， et al. Three-dimensional turbulent optimization of vaned diffusers for centrifugal compressors based on metamodel-assisted genetic algorithms[J]. Optimization and Engineering， 2014， 15（4）: 973－992.

[9] 曹安国，吴亚东，刘鹏寅，等. 基于改进Kriging代理模型的自适应序列优化算法在离心压缩机蜗壳设计中的应用[J]. 动力工程学报，2015，35（7）：562－567. Cao Anguo， Wu Yadong， Liu Pengyin， et al. Application of adaptive sequential optimization algorithm based on Kriging surrogate model in design of centrifugal compressor volute[J]. Journal of Chinese Society of Power Engineering， 2015，35（7）: 562－567. （in Chinese with English abstract）

[10] 王文杰，袁寿其，裴吉，等. 基于 Kriging 模型和遗传算法的泵叶轮两工况水力优化设计[J]. 机械工程学报，2015，51（15）：33－38. Wang Wenjie， Yuan Shouqi， Pei Ji， et al. Two-point hydraulic optimization of pump impeller based on Kriging model and neighborhood cultivation genetic algorithm[J]. Journal of Mechanical Engineering， 2015， 51（15）: 33－38. （in Chinese with English abstract）

[11] 王春林，叶剑，曾成，等. 基于NSGA-Ⅱ遗传算法高比转速混流泵多目标优化设计[J]. 农业工程学报，2015，31（18）：100－106. Wang Chunlin， Ye Jian， Zeng Cheng， et al. Multi-objective optimum design of high specific speed mixed-flow pump based on NSGA-Ⅱgenetic algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2015， 31（18）: 100－106. （in Chinese with English abstract）

[12] 袁寿其，王文杰，裴吉，等. 低比转数离心泵的多目标优化设计[J]. 农业工程学报，2015，31（5）：46－52. Yuan Shouqi， Wang Wenjie， Pei Ji， et al. Multi-objective optimization of low-specific-speed centrifugal pump[J]. Transactions of the Chinese Society of Agricultural Engineering （Transactions of the CSAE）， 2015， 31（5）: 46－52. （in Chinese with English abstract）

[13] Cadirci S， Selenbas B， Gunes H. Optimization of a centrifugal fan impeller using Kriging simulated annealing[C]// ASME 2011 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers，Denver， Colorado， USA， 2011: 991－997.

[14] 杨魏，王福军，王宏. 离心风机叶片三维反问题优化设计[J].农业机械学报，2012，43（8）：105－109. Yang Wei， Wang Fujun， Wang Hong. Aerodynamic optimization design of centrifugal fan blades based on 3-D inverse design method[J]. Transactions of the Chinese Society for Agricultural Machinery， 2012， 43（8）: 105－109. （in Chinese with English abstract）

[15] Ren G， Heo S， Kim T H， et al. Response surface methodbased optimization of the shroud of an axial cooling fan for high performance and low noise[J]. Journal of Mechanical Science and Technology， 2013， 27（1）: 33－42.

[16] Kim J H， Ovgor B， Cha K H， et al. Optimization of the aerodynamic and aeroacoustic performance of an axial-flow fan[J]. AIAA Journal， 2014， 52（9）: 2032－2044.

[17] Mann A， Pérot F， Kim M S， et al. Advanced noise control fan direct aeroacoustics predictions using a Lattice-Boltzmann method[J]. AIAA Paper， 2012， 2287: 2012.

[18] Sorguven E， Dogan Y. Acoustic optimization for centrifugal fans[J]. Noise Control Engineering Journal， 2012， 60（4）: 379－391.

[19] Yang Zhendong， Gu Zhengqi， Wang Yiping， et al. Prediction and optimization of aerodynamic noise in an automotive air conditioning centrifugal fan[J]. Journal of Central South University， 2013， 20（5）: 1245－1253.

[20] 陈懋章. 粘性流体动力学基础[M]. 北京：高等教育出版社，2002：290－301.

[21] Farassat F. Acoustic radiation from rotating blades-the Kirchhoff method in aeroacoustics[J]. Journal of Sound and Vibration， 2001， 239（4）: 785－800.

[22] Khelladi S， Kouidri S， Bakir F， et al. Predicting tonal noise from a high rotational speed centrifugal fan[J]. Journal of Sound and Vibration， 2008， 313（1）: 113－133.

[23] Wang Xiaofeng， Xi Guang， Wang Zhiheng. Aerodynamic optimization design of centrifugal compressor's impeller with Kriging model[J]. Proceedings of the Institution of Mechanical Engineers， Part A: Journal of Power and Energy，2006， 220（6）: 589－597.

[24] 刘城，潘鑫，闫清东，等. 基于DOE及RSM的液力变矩器叶片数对性能的影响及优化[J]. 北京理工大学学报，2012，32（7）：689－693. Liu Cheng， Pan Xin， Rui Qingdong， et al. Effect of blade number on performance of torque converter and its optimization based on DOE and response surface methodology[J]. Transactions of Beijing Institute of Technology， 2012， 32（7）: 689－693. （in Chinese with English abstract）

[25] Deb K， Pratap A， Agarwal S， et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. Evolutionary Computation， IEEE Transactions on， 2002， 6（2）: 182－197.

[26] Kang Qiang， Zuo Shuguang， Wei Kaijun. Study on the aerodynamic noise of internal flow of regenerative flow compressors for a fuel-cell car[J]. Proceedings of the Institution of Mechanical Engineers， Part C: Journal of Mechanical Engineering Science， 2014， 228（7）: 1155－1174.

Multi-objective parameter optimization of centrifugal compressor impeller with Kriging model

Zuo Shuguang, Wei Kaijun, Wu Xudong※, Nie Yujie, Xu Sichuan
（Cleɑn Energy Automotive Engineering Center, Tongji University, Shɑnghɑi 201804， Chinɑ）

Abstract:The high-speed centrifugal compressor used in the air supply system is the major noise source of the fuel cell vehicle. Therefore， it is important for the compressor to achieve low noise level as well as high compression ratio and efficiency. This paper presents an optimal design method for the centrifugal compressors using numerical simulation， Kriging model and genetic algorithm at the operating point. The rotational speed at the operation point is 80 000 r/min， the mass flow rate is 0.08 kg/s， and the compression ratio is 1.65. The steady RANS simulations are preliminarily used to provide the performance maps as well as the consistent initial conditions for the subsequent unsteady simulations. Performance maps are compared between numerical and experimental results at 40 000 and 50 000 r/min， which show a good agreement. Next， the unsteady simulations are performed to calculate the sound power level of the compressor. In order to analyze the influences of the blade inlet angle， blade outlet angle， trailing edge angle， tip clearance and blade thickness on the compression ratio，isentropic efficiency and sound power level， the optimal Latin square design is adopted to create the sample space. Each one of the sample points is simulated with the presented numerical method. The results show that the tip clearance and blade thickness are 2 primary factors. The compression ratio and efficiency decline when the tip clearance and blade thickness decrease， while the sound power level rises. The front incline is found to be better than the back incline. The Kriging model is built to reflect the functional relationship between the impeller design parameters and the performance parameters. Then， the multi-objective optimization is conducted with the genetic algorithm based on the Kriging model instead of the numerical model. The errors of the compression ratio， isentropic efficiency and sound power level between the Kriging model and the numerical model at optimized point are 0.11%， 0.46% and 0.01%， respectively. The blade inlet angle， blade outlet angle，trailing edge inclined angle， tip clearance and blade thickness of the baseline design are 37°， 45°， 26.7°， 0.3 mm and 1.2 mm，and the optimized design are 35.226°， 50.863°， -2.465°， 0.365 mm and 0.611 mm， respectively. Compared with the initial design， the compression ratio and isentropic efficiency of the optimal design are increased by 3.56% and 1.02%， respectively and the sound power level is decreased by 3.79 dB. The sound pressure spectrums show that the noise at blade passing frequency decreases by 16 dB. The rotational frequency and its noise at the harmonic frequency as well as broadband noise at the 0-1 800 Hz and 10 000-16 000 Hz also decrease. The compression ratio and isentropic efficiency of the centrifugal compressor are also improved at the off-design points. Internal flow fields are analyzed to find out the mechanism of the improvements. The results show that the velocity distribution is more uniform and the secondary flows in the blade flow channel significantly decrease after optimization， which means that the mixing loss at the impeller outlet decreases. This research provides a reference for optimizing the acoustic behavior as well as the performance parameters of centrifugal compressors at the early design stage.

Keywords:models; optimization; impellers; centrifugal compressor; unsteady simulation; aerodynamic noise; Kriging model

通信作者：※吴旭东，男，江苏扬州人，助理教授，主要从事汽车NVH研究，上海 同济大学新能源汽车工程中心，201804。

作者简介：左曙光，男，湖南沅江人，教授，博士生导师，主要从事汽车NVH研究，上海同济大学新能源汽车工程中心，201804。

基金项目：国家重大科学仪器设备开发专项（2012YQ15025605）；国家863项目（2012AA110501）

收稿日期：2015-08-19

修订日期：2015-12-21

中图分类号：TH452

文献标志码：A

文章编号：1002-6819（2016）-02-0077-07

doi：10.11975/j.issn.1002-6819.2016.02.012