接近式光刻中基于条纹相位解析的掩模硅片面内倾斜校正研究*

佟军民 徐 锋 胡 松

(①许昌职业技术学院，河南 许昌461000；②中国科学院光电技术研究所，四川 成都 610209；③西南科技大学信息工程学院，四川 绵阳 621010)

接近式光刻中基于条纹相位解析的掩模硅片面内倾斜校正研究*

佟军民①②徐 锋③胡 松②

(①许昌职业技术学院，河南 许昌461000；②中国科学院光电技术研究所，四川 成都 610209；③西南科技大学信息工程学院，四川 绵阳 621010)

针对接近式光刻中掩模硅片面内倾斜提出一种条纹相位解析方法。该方法通过2D傅里叶变换结合2D汉宁窗对于掩模硅片在面内发生的倾斜而形成的倾斜条纹进行处理，获得掩模硅片在面内的倾斜角度，进而进行倾斜校正。数值模拟与实验验证了该方法的可行性与有效性。结果表明，该方法能准确获得掩模硅片在面内的倾斜角度并进行校正。

纳米光刻；对准； 面内倾斜；条纹图形分析；相位解析

随着高集成度电路以及相关器件的研发，IC特征尺寸愈来愈小，对光刻分辨力要求也越来越高。如何提高光刻的分辨力成为业界关注的热点问题[1-4]。光刻对准技术作为光刻的核心技术之一，是影响光刻分辨力的重要因素之一，提高对准精度是提高光刻分辨力的一个重要途径[5-9]。基于光栅调制空间相位成像的纳米级对准方法[10-11]，理论上能达到较高的对准精度且具有最好的抗干扰能力。然而，掩模与硅片之间任意一点的倾斜将严重影响对准的精度。针对掩模硅片在空间内的倾斜，周提出了基于两周期相近的光栅作为标记的单点调平方法[12]，并且对掩模与硅片在两个正交方向的关系和倾斜条纹的相位分布进行了详细的介绍与讨论。但是，针对掩模与硅片在平面内的倾斜角度校正，却并未提及。因此，基于双光栅调平框架中掩模与硅片之间的面内相对倾斜，我们提出通过条纹相位解析方法对倾斜条纹图形进行处理来获得掩模硅片面内倾斜角度。首先，对基于双光栅对准中面内倾斜框架和条纹相位解析的原理进行了介绍；然后，通过数值模拟与实验验证了通过该方法进行倾斜位移与角度的提取的可行性与有效性；最后，给出了该方法的部分结果及面内倾斜校正精度的分析。

1 理论

1.1 面内倾斜干涉条纹

基于光栅调制空间相位成像纳米对准方法是采用了两周期接近的线形拼接微光栅作为掩模和硅片上的对准标记，将掩模与硅片的相对位置变化反映到条纹图像的空间相位变化中，通过CCD采集到干涉条纹图像，再解析条纹图像的空间相位信息，可以获得掩模与硅片的相对位移信息，用于进一步的对准。图1显示了基于光栅调制空间相位成像接近式纳米对准示意图。

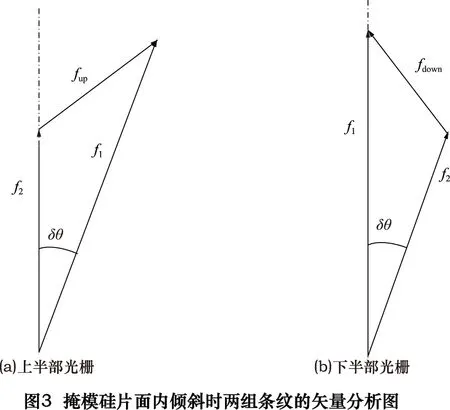
对准过程中掩模、硅片上的对准标记采用如图2所示的顺序相反(周期不同)的拼接光栅组成。掩模标记上半部周期为T1，下半部周期为T2；而硅片标记则相反，在对准过程中，上下两部分条纹分别进行对准，即图2a中周期为T1的光栅与图2b中周期为T2的光栅进行对准，而下半部分也相同。最终将形成两组运动方向相反的线形差动莫尔条纹。根据线光栅的莫尔成像规律可知，当如图2所示两光栅在平面内存在一定的旋转倾斜角度时，条纹分布频率与坐标系内的倾斜角可由条纹的波矢量大小与辐角表示[10]。这里，矢量描述的方向为光栅的延伸方向。如图3所示，当掩模与硅片在面内形成一个角度偏差δθ，两组光栅标记上下两部分产生的上下两组条纹向相反方向偏转。其中，上半部标记是频率为f1的光栅相对于频率为f2的光栅偏转；在下半部标记，频率为f2的光栅相对于频率为f1的光栅偏转。同时上下两组光栅产生的条纹满足一定矢量关系。两部分标记产生的矢量可分别表示为

(1)

(2)

由上式可推导出上下两组条纹相对于光栅延伸方向的夹角的正切值分别为

(3)

(4)

图4a-c给出了不同的掩模硅片面内角度偏移产生的条纹图像。图4d为掩模硅片两标记在面内没有倾斜产生的条纹图像。根据式(3)和(4)，当获得上下两组条纹的倾斜角度θup和θdown时，面内倾斜角度δθ将被计算出来。

1.2 倾斜条纹相位解析

我们提出一种结合2D傅里叶变换和2D汉宁窗的方法来进行相位解析，首先，条纹图形可归一化为

I=cos(2πF·X+φ0)

(5)

再对条纹进行2D傅里叶变换

+φ0)e-j(2π/M)uxe-j(2π/N)vy

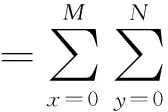
e-j(2π/M)uxe-j(2π/N)vy

(6)

式中：u、v为频域中的变量；M、N为条纹图形在两个方向的像素点；F(u,v)为经过2D傅里叶变换处理后的空间频谱。由式(6)可知，经傅里叶变换后的条纹频谱图与倾斜量造成的频率变化与倾斜角度有关。在频域中，θf表示基频点与u轴夹角。然后，再通过仔细设计2D汉宁窗来提取条纹分析后的有效频率部分。汉宁窗的函数被设置为：

(7)

式中：T1和T2分别表示在频域中沿着u和v轴的提取范围。最终，当获得条纹图像的相位之后，由于倾斜的影响，从条纹相位的任意一点开始分别沿着u和v轴移动相同的像素点其相位值是完全不同并产生一定的差值，而角度θ可以通过相位差获得，他们可表示为

(8)

式中：φAB和φAC分别表示沿着u和v轴从A点到B点和C点的相位差。同理可得出第二组倾斜条纹与水平方向的夹角，最后通过式(3)与式(4)获得掩模与硅片平面内的倾斜角度。

2 数值模拟

首先通过计算机模拟实现如图3所示的周期分别为2 μm与2.2 μm的双线光栅。当硅片相对于掩模在面内倾斜一定的角度时，将产生如图5a所示的条纹。在此，为了便于处理，条纹图像的大小选择为128pixel×256pixel。并且预设掩模和硅片的旋转角度为π/100，即0.031 416 rad。从图5a中可看出产生的上下两组条纹与垂直方向均产生一定的角度变化。为了便于验证，根据式(5)～(8)计算出条纹的频率和倾斜角度。其中，上面一组条纹偏离垂直方向角度θup为0.334 36 rad，下面一组条纹偏离垂直方向θdown为-0.302 94 rad(此处以条纹逆时针偏转为正)。为了更接近真实处理环境，在仿真中加入了均值为0、方差为0.3的高斯噪声，如5b所示。首先，对条纹图进行图像分割，获得如图5c所示上下两组条纹图；然后分别对上下两组条纹图应用二维傅里叶变换与改进的2D汉宁窗函数进行相位提取，再应用相位展开可获得各自条纹的连续相位分布。图6a、b分别为图5c所示上面一组条纹的包裹相位与展开相位图。最后，根据式(8)，角度θ可以通过φAB和φAC获得。角度θup为0.333 95 rad，该测量值与数值模拟中计算出角度相差为0.000 41 rad。同理，针对于下一组条纹，角度θdown为-0.302 21 rad，测量值与仿真中角度相差为-0.000 73 rad。从结果可知，条纹相位解析方法能很好地提取微小的面内倾斜位移用于校正。

3 实验

为了验证相位提取方法在实际应用中的有效性，我们依据图1所示的对准示意图搭建了实验平台。通过CCD采集到的条纹如图7所示分别为周期是2 μm与2.2 μm、6 μm与8 μm拼接光栅在面内发生倾斜时的条纹图。从图中可看出光学抖动与硅片工艺等所引入的噪声对条纹具有较大的影响。为了方便于图像处理，此处条纹截取为128pixel×256pixel。通过对图7分别应用2节所提面内倾斜条纹处理方法。首先进行图像分割，再通过2D傅里叶变换与改进的2D汉宁滤波器最终获得条纹包裹相位如图8所示。从包裹相位中可看出，条纹的相位也发生了倾斜，由于边缘部分相位易受到影响，通过对上面一组条纹的连续相位中间部分都取相隔80个像素值的相位差进行角度计算，最终获得周期为2 μm与2.2 μm条纹的倾斜角度为-0.142 0 rad，而周期为6 μm与8 μm条纹的倾斜角度为0.048 9 rad。然后通过式(3)获得掩模硅片上光栅标记的相对偏移角度，最终进行校正，获得的条纹图如图9所示。从图中可看出条纹的面内角度倾斜已基本校正，只存在横向位移的变化。

4 讨论

和数值模拟中的条纹进行对比分析可知，即使实验中的条纹严重受到外部因素的影响，条纹角度仍然能够通过文中所述的方法提取出来进行进一步提取倾斜角。通过该方法能很好地消除两组光栅标记在面内的倾斜。此外，根据式(3)和(4)可知，当其他的物理参数f1和f2确定后，面内倾斜校正的精度主要取决于条纹相位解析的精度。而根据公式(8)，相位解析的分辨率主要取决于条纹图像的大小。比如，当条纹图像的大小为256 pixels×256 pixels，当沿着u轴和v轴分别移动1个像素和200个像素达到相同的相位差，则条纹倾斜角度θf为0.005 rad。如果条纹图像更大，相位解析角度的分辨率将更高。其条纹倾斜角度探测灵敏度还会更高。而根据条纹角度式(3)可知，当面内倾斜角度δθ较小且趋近于0时，其与θf满足以下关系

(9)

此式表明条纹倾斜角度相对于掩模、硅片面内倾斜角度有一个线性放大作用，以周期为2 μm与2.2 μm的光栅为例，该放大倍率大约为10倍，通过前面所述倾斜条纹图像相位解析方法可获得大约0.000 5 rad的角度测量，由此可知，通过莫尔条纹相位解析可获得较高的角度探测灵敏度。

5 结语

针对接近式光刻对准过程中两光栅标记面内倾斜产生的倾斜条纹图形，提出了条纹相位解析方法来提取面内倾斜产生的倾斜角。该方法结合2D傅里叶变换和2D汉宁窗来获得条纹的倾斜角度。对掩模和硅片的对准框架和倾斜条纹相位解析进行了理论分析。然后通过数值模拟和实验验证了该方法的有效性。结果表明，该方法能准确提取条纹的倾斜角度并进一步计算掩模和硅片的面内倾斜角进行校正。并且通过该方法可以在接近式光刻中使掩模与硅片面内倾斜校正的灵敏度达到10-4rad甚至更高。

[1]Jain T, Aernecke M, Liberman V,et al. High resolution fabrication of nanostructures using controlled proximity nanostencil lithography[J]. Applied Physics Letters,2014,104(83117): 083117 - 083117-5.

[2]Huang J, Fan D, Ekinci Y,et al. Fabrication of ultrahigh resolution metal nanowires and nanodots through EUV interference lithography[J]. Microelectronic Engineering,2015, 141:32-36.

[3]Katrin S, Villanueva LG, Oscar VM, et al. Compliant membranes improve resolution in full-wafer micro/nanostencil lithography [J]. Nanoscale,2012,4(3): 773-778.

[4]Waiz K, Simon T Andreas, Mehtap O, et al. High-resolution and large-area nanoparticle arrays using EUV interference lithography [J]. Nanoscale,2015,7(16): 7386-7393.

[5]Li N, Wu W, Chou SY. Sub-20-nm alignment in nanoimprint lithography using Moire fringe [J]. Nano Letters,2006,6(11): 2626-2629.

[6]Wangfu C, Wei Y, Song H,et al. Extended dual-grating alignment method for optical projection lithography [J]. Applied Optics,2010, 49(4):708-713.

[7]Fader R, Rommel M, Bauer A,et al. Accuracy of wafer level alignment with substrate conformal imprint lithography [J]. Journal of Vacuum Science & Technology B,2013,31(6): 06FB02-06FB02-5.

[8]Nan W, Wei J, Jiangping Z,et al. Influence of collimation on alignment accuracy in proximity lithography[J]. IEEE Photonics Journal,2014,6(4): 1-10.

[9]Jiangping Z, Song H, Junsheng Y,et al. Influence of tilt moiré fringe on alignment accuracy in proximity lithography [J]. Optics and Lasers in Engineering,2013,51(4): 371-381.

[10]Shaolin Z, Yongqi F, Xiaoping T, et al. Fourier-based analysis of moiré fringe patterns of superposed gratings in alignment of nanolithography [J]. Opt. Express,2008,16(11): 7869-7880.

[11]周绍林,杨勇,陈旺富,等.基于双光栅的纳米测量方法[J].光学学报, 2009,29 (3):702-706.

[12]Shaolin Z, Yong Y, Lixin Z, et al. Tilt-modulated spatial phase imaging method for wafer-mask leveling in proximity lithography[J]. Optics Letters,2010, 35(18):3132-4

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Tilt correction in the plane between mask and wafer based on fringe phase analysis in proximity nanolithography

TONG Junmin①②, XU Feng③, HU Song②

(① Xuchang Vocational College, Xuchang 461000, CHN；② Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, CHN；③ Faculty Information & Engineering, Southwest University of Science and Technology,Mianyang 621010, CHN)

The fringe pattern phase analysis method is proposed for the tilt correction in the plane between mask and wafer in proximity lithography. The tilt between mask and wafer in the plane is reflected in the tilted fringe pattern. The method combining the 2D Fourier transform and 2D Hanning window is proposed for processing the tilted fringe pattern. The angles in the plane of tilt are extracted through phase analysis and the tilts are corrected. Computer simulation and experiment are both performed to verify this method. The results indicate that the tilt of the mask and wafer in the plane can be extracted with high accuracy through this method.

nanolithography; alignment；tilt in the plane; fringe pattern analysis; phase demodulation

*国家自然科学基金资助项目(61204114、61274108、61376110)；四川省教育厅基金资助项目(16ZB0141)

TH741.6

A

10.19287/j.cnki.1005-2402.2016.09.020

佟军民，男，1969年生，硕士，副教授，从事微电子专用设备技术方面的研究，已发表论文10篇。

�颖) (

2016-04-12)

160925