数字农业图像在小波变换中信号滤波步骤
2016-03-21易大国
曾 辉,易大国,2,卓 辉,方 逵*
(1.湖南农业大学信息科学技术学院,湖南长沙 410128;2.湖南生物机电职业技术学院,湖南长沙 410128)
1 小波因子值域信号与噪声的去噪
当前,小波分析-信号滤波在数字图像处理领域应用越来越广泛,其应用领域包括图像的压缩、去噪、边缘检测、增强[1]等。通常在频域中信号与杂波噪声散布区域明显不同,主要体现在高频区域中存在图像纹理、边缘轮廓等细节以及大量噪声;在低频区域基本是信号的分布[2]。如将信号与噪声两者重叠交集范畴变得尽可能小,或者变得比较大,这将对信号失真、噪声冗余、图像细节丢失造成很大负面作用;为此,既能保持图像细节特征又能很好消除掉噪声;如何有效将高频与低频区域内分布的细节、噪声、信号进行区分;成为图像去噪的关键。
其具体去噪过程为:定义原始图像为f(m,n),p(m,n),q(m,n)分别去高斯白噪声、噪声干扰后的图像,则关系表达式为:
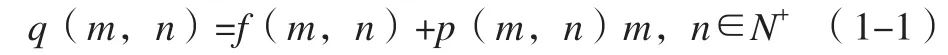
若式(1-1)为可离散小波,令其变换矩阵为W;则有:
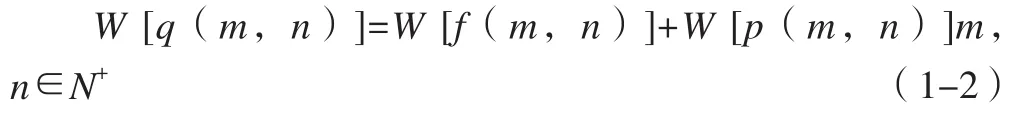
为便于对原理进行分析,令p(m,n)=P;f(m,n)=F;q(m,n)=Q且有Q=F+P
通过小波变换处理p(m,n)=P后仍然是Gaussian分布,换句话说就是高斯白噪声均匀散落在频率尺度全部空间中;而变换后的信号散落在频率尺度局部空间中,在能量有限角度出发:即受污染图像的噪声集中全部小波因子上,而信号能量集中在部分小波因子上。为此,小波因子大体可分为两种:(1)受污染噪声小波变换后产生的,数量小、此时波峰到波谷距离的一半(即幅值大);(2)信号变换后的幅值小,数量多。故可以根据幅值参数不同,来设置一个临界值,来去除图像噪声部分,与此同时,很好保存图像局部细节特征。
2 小波片分量编码——解码图像压缩
小波变换处理后的图像压缩可在离散余弦变换基础上降低“块状噪声”“随机噪声”以及“蚊式噪声”作用[3];即通过时频域局部分析方法不但可将图像片分量与视觉效果中的多层分辨率,方向异同的信号频带去相关性编码相匹配,而且经过变换后将大多数小波系数信号集中在某些子带,这将对图像的压缩更加有利。
利用小波变换对图像进行压缩时,首先将初始图像进行分量分解;同时常常需要先考虑图像的大小,若图像较大时,需将分解后分量图划分为若干个信号片,若图像较小,可将整个图片看成一个信号片。在此过程(如图1所示),初始图像和分量分解图像的最小基本单位为信号片。这样划份多个段信号片能防止“方形块状”效应的产生。随后,信号片经过小波变换后再次分解成多个分辨等级次序,而其中分辨等级次序最小组成单元为信号频带去相关编码带。值得关注的是去相关性后的编码带变换系数能体现分辨级别、片分量的频域特点。接着对该系数进行“编码块”矩阵量化,在此过程中编码块中的位平面按关键性次序从主到次进行系数信息量度量的嫡编码,得到压缩码流,为方便对编码错误修复,故而在码流中添加特殊标识符号。最终,在产生的码流前方存在一段头消息,用来解释初始图像的分解等级次序;解码端会根据上面的头信息,结合自身实际情况,无需解出所有码流,就能够重新构建出关于初始图像在某个特定分辨率下、某一特定区域中的图像。
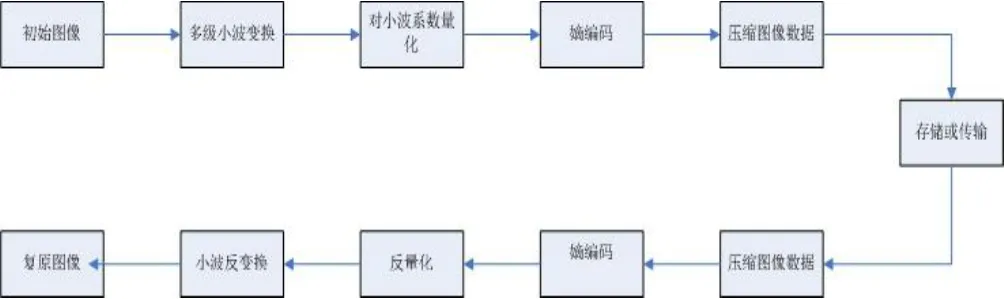
图1 小波变换图像压缩过程
3 小波变换尺度分量——图像增强
由于小波变换自身具有多分辨率和双尺度等特点,是在能够满足图像与视觉相匹配的要求情况下诞生的,其旨在有目的性地凸显图像感兴趣部分或者去除噪声的特征。根据小波变换尺度分量特性,可分为对角高频、垂直高频、水平高频、低频分量[4]。考虑到图像增强处理的实际情况,对不同空间结构、不同的能量载波以及不同坐标方向的分量来改变小波因子的数值,达到某些感兴趣特征分量放大、去噪部分分量缩小的目的。一般情况下,都是通过小波变换对高频分量的小波因子进行改变,从而能够有效增强图像质量、丰富图像的信息量。
常见的小波变换图像增强方法有空域法和频域法,其中前者是就图像的像素点进行讨论的,即:
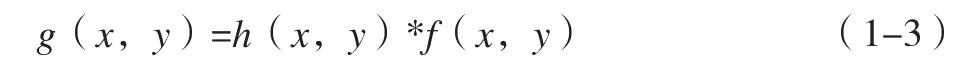
式(1-3)f(x,y)为初始图像函数,h(x,y)是空间转换函数,g(x,y)代表处理后的函数。
而频域法小波变换增强原理:先将频域内对图像进行傅立叶变换,然后对图像的频谱数字滤波修复,最后,将修正后的图像进行傅立叶反变换,使得图像感兴趣特征得到进一步增强(如图2所示)。

图2 图像增强——频域模型
4 小结
本文分别就基于小波系数大小的数字农业信号与噪声、数字农业图像细节特征去噪、数字农业图像压缩以及小波尺度分量做了详细介绍;这将对后期研究农业数字图像中存在脉冲噪声、Gaussian噪声、以及混合噪声具有重要作用。
[1] 易大国,曾辉,卓辉,等.农业物联网数字图像传输—小波变换信号滤波处理研究[J].农业网络信息,2015(11):44-48.
[2] 王晓甜.基于信噪特征的遥感图像去噪方法研究[D].西安:西安电子科技大学,2011.
[3] 金彩虹.小波域内的分形图像编码[D].武汉:华中师范大学,2001.
[4] 邢小军.小波变换边缘检测及边缘线特征描述算法研究[D].南昌:南昌航空大学,2011.
