立式水轮发电机组转动部件和负荷机架联合系统的轴向固有频率分析

汪 小 芳（东芝水电设备（杭州）有限公司，杭州 310020）



立式水轮发电机组转动部件和负荷机架联合系统的轴向固有频率分析

汪 小 芳
（东芝水电设备（杭州）有限公司，杭州 310020）

[摘要]对立式水轮发电机组转动部件和负荷机架联合系统的轴向固有频率进行了单自由度系统和二自由度系统的理论分析，并用有限元方法进行了解析对比研究，发现固有频率的理论分析结果略高于有限元解析值，但是两者误差在1%以内；并且根据分析结果，提出了单自由度系统和二自由度系统各自的适用范围，为转动部件和负荷机架联合系统的轴向固有频率的有效评估提供了参考。

[关键词]水轮发电机；转动部件；负荷机架；二自由度系统；固有频率；有限元法

0　引言

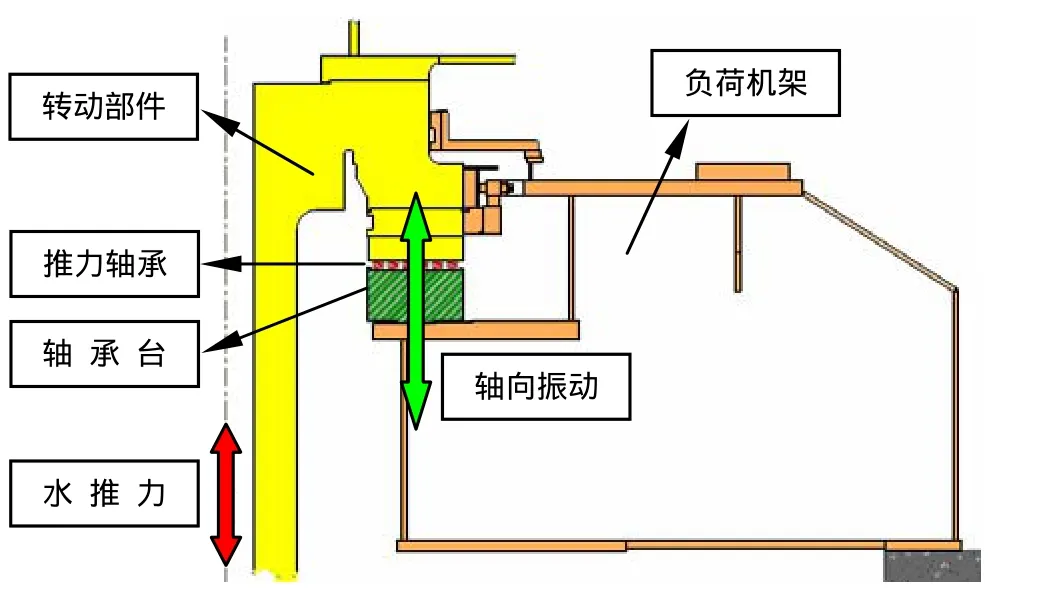
图1　转动部件轴向振动

如图1所示，立式水轮发电机组的转动部件通过推力轴承安装于负荷机架上。运行过程中，作用于转轮的轴向水推力经转动部件最终传递到推力轴承。由于水推力的周期性变化，整个转动系统将会产生一定程度的轴向振动。如果该振动频率和转动部件与负荷机架组成的联合系统的固有频率接近，就会导致机组轴向共振，严重时甚至引发安全事故。因此，在设计阶段，需要对转动部件和负荷机架组成的系统作轴向固有频率计算。

1　理论计算

转动部件坐落于推力瓦上，运行过程中，两者之间会产生推力油膜。

推力瓦通常通过其下部的弹性支撑元件，比如弹性油箱或者弹簧簇等，安装于轴承台上。

轴承台放置在负荷机架上。

在轴向振动系统中，转动部件和轴承台就是简谐振子，而推力油膜、弹性支撑以及负荷机架就是弹簧部件。所以，转动部件与负荷机架所组成的振动系统可以简化为如图2所示的模型。

符号说明：m1：转动部件重量，t；m2：轴承台重量，t；KOIL：推力油膜轴向刚度，t/mm；KSP：弹性支撑轴向刚度，t/mm；KZ：负荷机架轴承台支撑部位的轴向刚度，t/mm；由有限元计算得到。

K1：推力油膜与弹性支撑串联之后的合成刚度，t/mm；K2：为便于记号统一，将KZ记作K2，t/mm；g：重力加速度，9800 mm/s2；

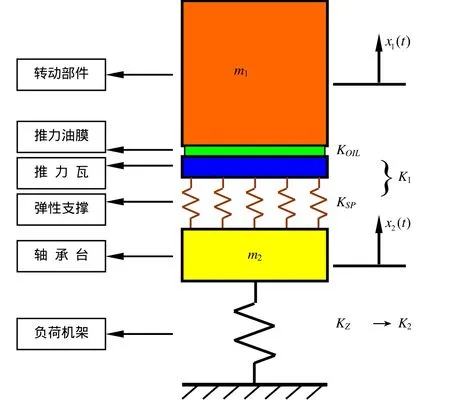
图2　轴向振动系统模型

1.1单自由度系统

当轴承台重量远小于转动部件重量时，整个振动系统可以进一步简化为单自由度系统。此时简谐振子质量m、弹簧刚度K如下式表示

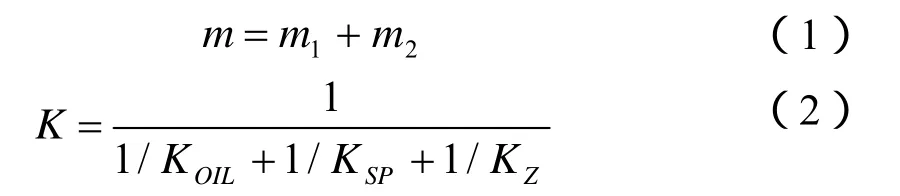
从而，转动系统的轴向固有频率f为

1.2二自由度系统

当需要考虑轴承台重量时，整个振动系统即为二自由度系统。此时，由图2可知，与振子m1、m2对应的弹簧刚度K1与K2分别为

令x1(t)、x2(t)分别为转动部件和轴承台的位移，单位mm。

运用牛顿第二定律，分别对m1和m2列竖直方向的运动方程：

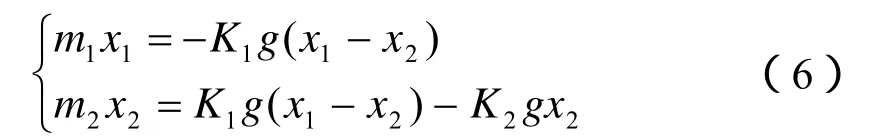
即，

写成矩阵形式，即为

式中，

设解为

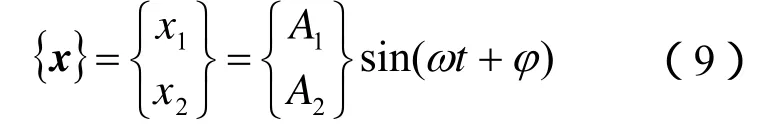
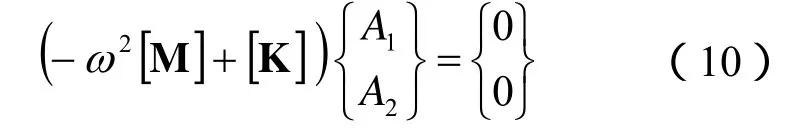
因为A1、A2不为0，所以有

即，

展开即可得到关于w2的一元二次方程

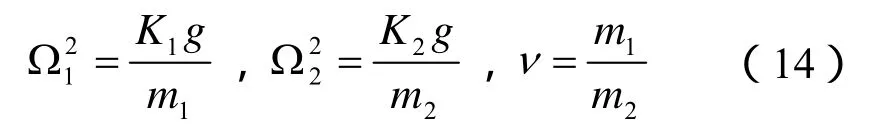
则有，

该一元二次方程的两个根为

所以，前二阶固有频率为

另外，由式（10）可得

所以，模态向量为

2　有限元计算

上述理论分析的缺点是将负荷机架简化成了轻质弹簧。显然，负荷机架由于结构的复杂性，无法简化为一个不计重量的弹簧，所以，上述计算得到的频率结果偏大。

为了更准确地得到整个振动系统的固有频率，也为了评估机架重量的影响，下面采用有限元方法进行计算。

图3　转动系统轴向振动解析模型

典型水轮发电机转动系统轴向振动解析模型如图3所示。在机架轴承台支撑部位建立轴向的弹簧单元，用以模拟推力瓦下部的弹性支撑。在轴心部位建立质量单元，用以模拟整个转动部件的质量。

弹簧单元的下部端节点与机架合为一体，而上部端节点则与代表转动部件的质量单元所在节点形成刚性连接。质量单元节点为主节点，所有弹簧节点为从节点，从属自由度为轴向平动。

在需要考虑轴承台质量的情况下，需要在机架轴承台支撑部位建立分布的质量单元，而且这些质量单元成为弹簧单元的下部端节点。

然后，对机架支臂基础板部位施加固定的位移边界条件之后，即可对整个系统进行有限元模态分析，得到转动部件的轴向固有频率。

3　计算结果分析

分别用单自由度、二自由度及相应的有限元方法计算了几个电站的转动部件和负荷机架联合系统的轴向固有频率，结果见表1。

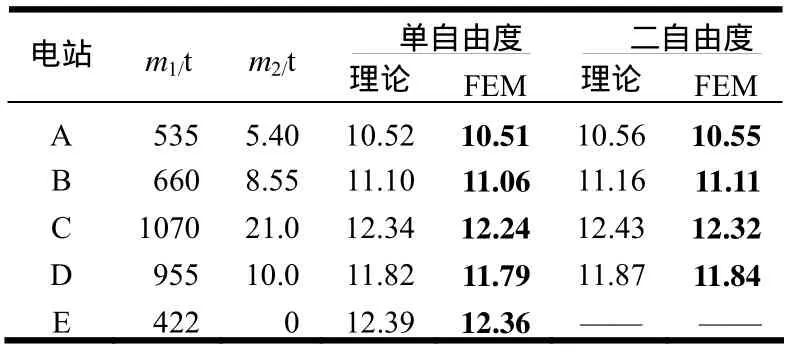
表1　轴向固有频率计算结果对比　Hz

从表1可以看出，无论是单自由度还是二自由度，理论计算的结果都略高于有限元解析，但是两者的偏差都在1%以内。这也就说明机架自身重量对计算结果的影响可以忽略不计。

另外，计算的几个案例中，轴承台的重量相对于转动部件而言，都非常小。此时，二自由度系统的一阶固有频率比单自由度系统时略高，但是两者的偏差也在1%以内。所以，当轴承台重量较小时（转动部件重量的1/10以下），单自由度系统的理论计算结果完全可以评估整个转动系统的轴向固有频率。

为了研究需要，不妨看一下轴承台重量占比较大时的结果对比情况。

以A电站为例，假设轴承台重量为200t，则计算结果对比如表2所示。

表2　轴承台重量较大时计算结果对比　Hz

由上表可以看出，一阶固有频率结果，二自由度系统的理论值10.14 Hz与有限元解析值10.12 Hz的误差只有0.2%。而此时若是根据单自由度的理论公式进行计算，得到的结果则为9.02 Hz，与解析结果偏差近20%。所以当轴承台重量与转动部件重量处于同一数量级时，必须采用二自由度系统进行固有频率的分析计算。

此算例，二自由度系统的一阶模态与二阶模态分别如图4、5所示。

有限元结果中，比较弹簧单元上、下部节点的振幅值，即可得到幅值比A2/A1。

由图4可知，一阶固有振型中：

A2/A1= 0.021/0.041 = 0.51

这与理论计算的0.50非常接近。

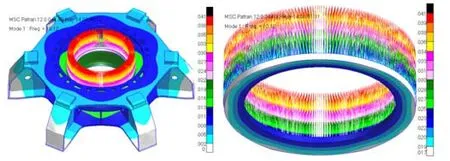
图4　一阶固有振型（10.12Hz）

图5　二阶固有振型（35.27Hz）

由图5可知，二阶固有振型中：

A2/A1= -0.069/0.013 = -5.31

这与理论计算的-5.31一模一样。

所以，在考虑轴承台重量的二自由度系统计算中，理论计算结果完全可以评估转动部件的轴向固有频率。

4　结语

通过对立式水轮发电机转动部件和负荷机架联合系统轴向固有频率的理论分析和有限元对比解析研究，可以得到以下结论：

（1）在没有轴承台，或者轴承台重量可以忽略的情况下，单自由度系统的理论分析结果略高于有限元解析值，但是误差在1%以内。

（2）当轴承台重量与转动部件重量接近于同一数量级时，必须按二自由度系统来考虑。此时，一阶固有频率的理论分析结果也略高于有限元解析值，但是误差也在1%以内。

（3）在轴承台重量较大时，二阶固有频率也是十分重要的。此时，轴承台的振动频率也有可能引起结构的轴向共振，必须引起注意。

（4）当计算得到的固有频率与转轮水推力的激振频率的偏差在±20%的范围之内时，必须通过调整负荷机架结构以改变机架的轴向刚度，最终使得激振频率与固有频率不发生共振。

汪小芳（1978-），男，2004年毕业于浙江大学固体力学专业，硕士，主要从事水轮发电机设计和有限元解析工作，高级工程师。

审稿人：钟苏

水轮机及水泵

Analysis of Axial Natural Frequency of the Combined System of Rotating Parts and Thrust Bearing Bracket of Vertical Hydro-generator

WANG Xiaofang
(Toshiba Hydro Power (Hangzhou) Co., Ltd., Hangzhou 310020, China)

Abstract:The single-degree-of-freedom system and two-degrees-of-freedom system theory have been used to analysis the axial natural frequency of the combined system of rotating parts and thrust bearing bracket of vertical hydro-generator, and finite element method also have been carried out for comparative study. It finds that the natural frequency results from theory are slightly higher than the finite element analytical value, but the difference is within 1%. According to the results of the analysis, the applicable scope of single-degree-of-freedom system and two-degrees-of-freedom system of their own is proposed, and then provide a reference for the effective evaluation of the axial natural frequency of the combined system.

Key words:hydro-generator, rotating parts; thrust bearing bracket; two-degrees-of-freedom system; natural frequency; FEM

[作者简介]

[收稿日期]2014-08-17

[中图分类号]TM312

[文献标识码]A

[文章编号]1000-3983(2016)01-0021-03