串级控制对过程预测控制的影响分析与对策

罗雄麟，叶松涛，许锋，许鋆（中国石油大学(北京)自动化系，北京 102249）



串级控制对过程预测控制的影响分析与对策

罗雄麟，叶松涛，许锋，许鋆
（中国石油大学(北京)自动化系，北京 102249）

摘要：化工过程控制中普遍设置以流量控制为副回路的串级控制来实现对温度、液位和成分等被控变量的控制。预测控制的操作变量在很多情况下也是流量，其控制作用的实现要靠底层的流量控制回路。本文针对由于现场串级控制结构不允许改变，流量副回路只能接收温度等主控制器的输出作为其给定值，造成上层预测控制的操作变量无法直接下载到流量控制回路的问题，分别提出了一种将上层优化输出通过一阶惯性滤波作用于主回路控制器和一种将串级控制中流量对主被控变量的传递函数嵌入预测控制模型的实施方案，通过Shell标准重油分馏塔的控制问题进行仿真实验证明了两种方案的可行性，并对其控制性能进行了比较分析。两种方法理论上构思简单，实际中易于实现，具有普遍适用性。

关键词：过程控制；预测控制；串级控制；副回路；流量

第一作者及联系人：罗雄麟（1963—），男，博士，教授，研究方向为控制理论与过程控制工程、化工系统工程、模式识别与智能系统。E-mail luoxl@cup.edu.cn。

在过程控制领域中，模型预测控制（model predictive control，MPC）已经成为一种解决有约束多变量控制问题的标准技术与方法。目前的工业过程控制系统多数为多层递阶结构[1-3]，MPC作为系统承上启下的重要环节，基于上层的操作优化结果实施先进控制，其预测控制器的输出再送到底层多回路PID控制器的设定值，由底层PID控制实现，MPC的应用有助于提高工业生产过程的经济性和平稳性[4-6]。

多变量控制系统设定值的设计问题关系到工业生产过程的安全稳定性、产品质量、产品收率以及运行成本等诸多问题。对于MPC的设定值设计问题，文献[7]提出设定值的选取应该追求全局最优，而非仅仅对局部生产过程实现优化控制，从而达到提高品质和降低成本的目的。文献[8-9]指出化工过程控制中普遍存在着各种对输入和输出变量的约束条件，若由人工或通过工艺优化直接将设定值送入动态控制层后，设定期望值与系统约束之间的不相容可能使得控制目标无法实现，因此设定值的设计应包含其可行性的分析和不可行时的约束处理。文献[1-2，10-11]通过在常规MPC动态控制层上添加了一个稳态优化层，提出双层结构预测控制以解决多变量控制系统设定值的设计问题。

然而，对于底层多回路PID控制器的设定值设计问题却鲜有人关注，这是因为目前通常认为上层MPC控制器输出的操作变量都可以直接送到底层多回路PID控制器的设定值，必然能够通过底层的基本PID控制层来实现。但是，化工过程底层控制中对重要被控变量如温度、成分、液位等普遍设置以流量控制为副回路的串级控制[12-13]，而预测控制的操作变量在很多情况下也是流量[14-15]，故MPC控制器输出也应当送到流量控制回路的设定值上。在串级控制中流量控制在副回路中，作为副控制器只能接收温度等主控制器的输出，上层MPC控制器的输出不允许直接下载到串级控制副回路的流量控制器设定值上，使得上层预测控制无法实现。现有的解决方案通常是将现场的串级控制结构直接断开或者利用辨识建模，前者通过改变现场结构的方法虽然实施简单，但是取消主回路控制后无法有效保证主被控变量的控制效果，而且当预测控制停用检修或者撤除时，由于无法恢复原有的操作条件，给生产带来安全隐患。后者利用辨识建模的方法虽然具有普遍适用性，但其模型外推性较差，无法在多个同类生产上移植，而且所建的模型只能针对当时测试时的生产工况，工况变化太大，模型需要重新测试和辨识，尤其是辨识建模需要对工业装置进行大量的测试工作，对生产操作产生较大的干扰。

本文作者针对如何通过现存的“主被控变量-流量”串级控制实现流量在线优化问题，给出了一种流量优化变量通过一阶惯性环节改变主回路被控变量设定值的在线优化的理想方案[16]。在此基础上，本文基于预测控制机理建模，在不改变底层控制结构的条件下考虑通过现有的“主被控变量-流量”串级控制结构来实现过程预测控制输出的问题，分别提出了一种将上层优化输出通过一阶惯性滤波作用于主回路控制器和一种将串级控制中流量对主被控变量的传递函数嵌入预测控制模型的实施方案，并通过重油分馏塔的Shell标准控制问题进行仿真实验证明了两种方案的可行性。

1 问题提出

流量是化工过程中重要的调节变量，在化工领域，工艺装置中各单元设备中进行着复杂的物理过程和化学过程，这些过程都与流量的变化密切相关，因此通常通过流量的改变来实现化工过程中被控变量和操作指标的调节。预测控制的操作变量在很多情况下也是流量，特别是当预测控制的模型是通过机理分析的方法获取时，其建模过程的实质就是将质量衡算和能量衡算进行具体化，所建模型的输入变量是流量，输出变量是成分、液位、温度等。因此，预测控制最终输出一般为流量优化设定值，而流量优化设定值的实现最终又要靠底层的流量控制系统来实现。

另一方面，在化工过程控制中，由于流量作为重要的过程变量，其在生产过程中通常受到大幅高频扰动，因此实际生产中底层控制广泛采用串级控制结构，即将流量控制设置为副回路，设定值由主控制器输出决定，在流量副回路中抑制干扰因素，确保了主回路中温度、液位和成份等被控变量的控制品质。因此，如图1(a)所示，其表征了典型底层串级控制系统的结构当流量作为上层预测控制的操作变量时，由于串级控制回路副控制器的设定值不能直接由预测控制器输出给定，导致预测控制输出的实现存在问题。

如图1(b)所示，若将作为预测控制输出的流量设定值Fop直接叠加到流量副回路控制器Gc2的设定值上，副回路控制器将会接收到两个设定值信号，即设定值为主控制器输出Fsp和预测控制输出Fop之和。由于闭环反馈作用，经过若干控制周期后，系统达到稳态，主控制器Gc1输出值将改变至（Fsp−Fop），则流量副回路控制器设定值恢复至Fsp，达不到优化值Fop。而若将串级控制结构断开，取消主回路控制，让副回路独立工作，预测控制器代替了主控制器的功能，其输出直接作为副回路的控制器作为设定值。但这种方式改变了现场的控制结构，且无法保证主被控变量的控制效果，为生产工艺过程所不允许，因此需要寻找解决预测控制在串级控制中的实现方法。

2 控制方案实现

针对如图1中的预测控制面对串级控制结构的实现问题，本节提出了两种控制实现方案，并对其控制方案的原理及其优点进行了论述。

2.1 一阶惯性滤波实现方案

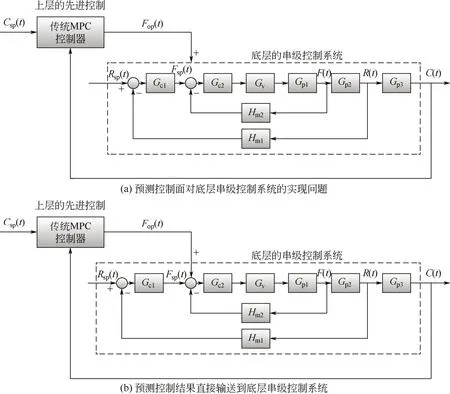
图1 过程预测控制面对串级结构的控制实现

图2 串级控制的预测控制实现结构

为了满足生产工艺，必须在不断开主回路的前提下，将预测控制输出作用于副回路控制器。可考虑将预测控制输出处理后作用于主回路控制器，且保证主控制器输出值达到副回路控制器的理想设定值，即将图1(a)中的控制结构图进行比较点前移的等效变换。根据串级控制中各个模块的传递函数，可推导出Fsp到Rsp的传递函数关系，见式(1)。

为了得到Fsp到Rsp的传递函数关系，可对G(s)进行求逆运算，即式(2)。

根据式(2)可将预测控制输出的流量设定值转化为主被控变量的设定值，然后作用于主回路。这样就解决了预测控制在串级控制中的实现问题。通过式(1)可知，G−1(s)在工程实际中使用存在两方面的问题：一方面由于其与串级控制中的PID参数有关，因此当控制参数发生变化时，G−1(s)也要进行更新；另一方面由于G(s)是根据实际物理单元建模得到，其精度不高且通常为真分式，导致G−1(s)的准确性以及物理可实现性难以保证。另外考虑到预测控制的优化结果一次性下载给对象会造成系统的大幅波动[17-19]。因此，可采用一阶惯性滤波器来简化代替G−1(s)，该过程必须保证一阶惯性环节的增益与G−1(s)相同且时间常数选择合理。该滤波器作用在于将预测控制输出的流量设定值Fop转化为主控制器设定值Rop，即式(3)。

该方案的系统控制结构如图2(a)所示。一阶惯性环节中的Kg可以通过闭环辨识得到，时间常数T可通过优化的方法得到最优值。综上，该方案能够在不改变现场串级控制结构的基础上，实现了上层预测控制。并且该方案具有实现简单、可靠性好、普适性强等优点。

2.2 嵌入底层串级动态信息的MPC控制

预测控制是基于模型的算法，通过机理建模获得的流量对MPC被控变量的传递函数矩阵为式(4)。

由于流量在石油化工工业的质量衡算和能量衡算中的重要地位，因此预测控制的操作变量通常以流量为主。面对化工过程中广泛存在着的“主被控变量－流量”串级控制回路，以流量作为操作变量的预测控制在输出实现上存在问题。假设由于底层的串级控制结构导致MPC控制器的第j个输出无法实现，通过辨识的方法获得第j个输出到其对应的串级控制结构中主被控变量的传递函数为Gj(s)，将流量对主被控变量的传递函数嵌入到预测控制模型中，得到主被控变量设定值对MPC被控变量的传递函数矩阵为式(5)。

系统控制结构如图2(b)所示。这种方法仅需对底层的串级控制中副变量对主变量的传递函数进行辨识，无需对整个生产装置进行生产测试和辨识，大大减少了工作量，对工艺生产的影响小。该方法简单易行且具有较强的通用性。

3 控制方案实现与对比分析

以壳牌公司的典型重油分馏塔控制问题为例进行研究，如图3所示，重油分馏塔有一个提供热量的气态过热蒸汽进料、3个产品抽出和3个侧线循环回流，包括3个控制变量（顶部抽出u1、侧线抽出u2和塔底回流负荷u3）、7个被控变量（塔顶馏出物终馏点y1、塔底馏出物终馏点y2、塔顶温度y3、顶部循环回流温度y4、侧线馏出物抽出温度y5、中部循环回流温度y6和塔底循环回流温度y7）、2个扰动量（塔顶循环回流负荷l1和中段循环回流负荷l2）。对于该系统Prett和Morari给出的一阶传递函数模型[20]，其变量控制约束见表1。

重油分馏塔是一个多变量、有约束的系统。其延迟时间长达28min，时间常数60min，动态响应时间约208min，可见该对象工艺结构复杂，其时变、强耦合、大时延、大时间常数、大动态响应等特点让它成为公认的比较难控的典型对象，现有的专家学者普遍利用此模型对各种新型控制方法进行测试[21-22]。重油分馏塔设备有3个被控变量：塔顶产品组成y1、侧线产品组成y2、塔底循环回流抽出温度y7，当操作变量为顶部抽出u1、侧线抽出u2和塔底回流负荷u3时，其过程模型的传递函数矩阵为式(6)。

通过在MATLAB软件平台上进行预测控制仿真实验，假设系统初始输入、输出为零，被控输出目标是将y1、y2和y7分别控制到0.2、−0.4、0.3，仿真曲线如图4(a)所示。可以看出，对于该多变量、有约束的复杂系统，实施预测控制能够取得较好的控制效果。

图3 重油分馏塔结构图

表1 Shell重油分馏塔变量约束

但是，在实际重油分馏塔的工业控制现场中，由于塔顶温度y3与塔顶馏出量u1以及侧线抽出温度y5与侧线抽出量u2强烈关联，且两个主要扰动为塔顶循环回流l1和中段循环回流l2，所以实际现场控制中通常分别对其采用串级控制结构，即建立y3–u1、y5–u2的串级控制。由于串级控制结构的特点，上层预测控制器输出的流量结果不允许直接送给副回路的控制器设定值，只允许送给主回路的控制器设定值，将会出现如图1所示的预测控制的实现问题。因此，依据上述模型的预测控制在现场实施时必须将底层串级结构的主回路断开，取消串级控制中的主控制回路，而对于绝大多数不允许改变底层控制结构的工业现场，这种采用打开底层串级控制结构的预测控制方案并不适用。

现利用表1中的过程模型在MATLAB/Simulink平台上搭建重油分馏塔仿真模型，调节PID参数以保证底层的串级控制性能最佳。对于底层的串级控制回路，通过闭环辨识可获得u1–y3和u2–y5的传递函数为式(7)。

首先采用通过一阶惯性环节改变主回路被控变量设定值的方法，依据辨识结果可知g1(s)和g2(s)的增益Kg1和Kg2分别为3.65和2.37，为使预测控制输出对主回路设定值的调整柔和平稳，最终选定时间常数T1和T2分别为15和25。

其次采用将串级控制中流量对主被控变量的传递函数嵌入预测控制模型的方法，根据式(5)可推导出嵌入流量对主被控变量的传递函数后的预测模型为式(8)。

将以下几种预测控制的实施方案分别进行仿真。

（1）将串级控制结构的主回路打开，预测控制模型以流量为输入，MPC被控变量为输出，预测控制操作变量直接送到流量控制回路的设定值上，仿真曲线如图4(a)所示。

（2）保留串级控制结构的主回路，预测控制模型以流量为输入，MPC被控变量为输出，预测控制操作变量通过一阶惯性环节改变主回路被控变量设定值，仿真曲线如图4(b)所示。

（3）保留串级控制结构的主回路，将串级控制中流量对主被控变量的传递函数嵌入预测控制模型，预测控制模型以主回路被控变量设定值为输入，MPC被控变量为输出，预测控制操作变量直接改变主回路被控变量设定值，仿真曲线如图4(c)所示。

（4）保留串级控制结构的主回路，以串级控制主回路的设定值作为输入变量，MPC被控变量作为输出变量，通过系统辨识的方法获得重油分馏塔的预测控制模型[式(9)]预测控制操作变量直接改变主回路被控变量设定值，仿真曲线如图4(d)所示。

将图4中的仿真结果进行对比得出，方案(2)和方案(4)的控制效果相似，对该多变量、有约束的复杂系统能够取得较好的控制效果，系统在360min左右达到控制目标；方案(1)和方案(3)的控制效果是相近的，而且在控制性能上优于前两种控制方案，系统在300min时达到控制目标。

图4 控制策略仿真曲线被控变量：y1—塔顶馏出物终馏点；y2—塔底馏出物终馏点；y7—塔底循环回流温度

方案(1)需要改变底层控制结构，常为工业现场所不允许，在工程应用中有较大的限制；方案(4)虽然具有普遍适用性，但其模型外推性较差，无法在多个同类生产上移植，而且所建的模型只能针对当时测试时的生产工况，工况变化太大，模型需要重新测试和辨识，辨识建模需要对工业装置进行大量的测试工作，将会对生产操作产生较大的干扰；相比之下，机理建模方法的适用范围宽、外推性好、对工艺生产影响小，在实际工业的应用中获得了良好的控制效果，但需要解决流量同时作为预测控制操作变量和串级控制副变量的实施问题。因此，本文针对实际工程中以流量为操作变量的预测控制，提出了方案(2)和方案(3)，并均获得了良好的控制效果。综合比较4种控制方案，方案(3)在保证普遍适用性的同时，获得了最佳的控制效果。本文所述普遍适用性就是这种控制方案的实施对任何底层常规串级控制都可以不必改变（重新组态）就可以实现上层的预测控制。

4 结 论

本文从预测控制实际应用出发，针对现场实施中如何在现存的“主控制变量–流量”这种典型的化工过程串级控制条件下实现预测控制的流量操作变量实施的问题，给出了一种通过一阶惯性环节改变主回路被控变量设定值和一种将串级控制中流量对主被控变量的传递函数嵌入预测控制模型的实施方案，两种方案构思简单，实际中易于实现，具有普遍适用性。通过Shell标准重油分馏塔控制问题进行控制方案的验证，分析了实际中现存的两种控制方案的适用限制问题，并与本文提出的两种控制方案进行仿真对比，证明本文提出的“将串级控制中流量对主被控变量的传递函数嵌入预测控制模型的实施方案”不仅解决了预测控制的流量操作变量在串级控制结构下的实施问题，具有较强的工程适用性，而且能够获得更佳的调控效果。

符 号 说 明

Csp—— 上层预测控制器设定值输入

Fop—— 上层预测控制器输出

Fsp—— 主控制器输出

Gc1—— 主控制器

Gc2—— 副控制器

Gp1—— 副被控对象

Gp2——主被控对象

Gv——调节阀对象

Hm1——主回路反馈环节

Hm2——副回路反馈环节

Rsp——主控制器设定值输入

l1——塔顶循环回流负荷，kmol/h

l2——中段循环回流负荷，kmol/h

u1——顶部抽出量，kJ/h

u2——侧线抽出量，kJ/h

u3——塔底回流负荷，kmol/h

y1——塔顶馏出物终馏点，K

y2——塔底馏出物终馏点，K

y3——塔顶温度，K

y4——顶部循环回流温度，K

y5——侧线馏出物抽出温度，K

y6——中部循环回流温度，K

y7——塔底循环回流温度，K

参 考 文 献

[1] QIN S J，BADGWELL T A. A survey of industrial model predictive control technology[J]. Control Engineering Practice，2003，11（7）：733-764.

[2] NIJANDROVL A，SWARTZ C L E. Sensitivity analysis of LP-MPC cascade control system[J]. Journal of Process Control，2009，19（1）：16-24.

[3] 邹涛，王丁丁，潘昊等. 从区间模型预测控制到双层结构模型预测控制[J]. 化工学报，2013，64（12）：4474-4483.

[4] CAMACHO E F. Constrained generalized predictive control[J]. IEEE Transactions on Automatic Control，1993，38（2）：327-332.

[5] WANG Y，BOYD S P. Fast model predictive control using on-line optimization[J]. IEEE Transactions on Control Systems Technology，2010，18（2）：267-278.

[6] LING K V，MACIEJOWSKI J，RICHARDS A，et al. Multiplexedmodel predictive control[J]. Automatica，2012，48（2）：396-401.

[7] CAO Z W，EASTERLING D R，WATSON L T，et al. Power saving experiments for large-scale global optimization[J]. International Journal of Parallel，Emergent，and Distributed Systems，2010，25 （5）：381-400.

[8] 张惜岭，罗雄麟，王书斌. 过程预测控制中约束可行性研究与在线调整[J]. 化工学报，2012，63（5）：1459-1467.

[9] 于洋，许鋆，罗雄麟. 预测控制约束边界效应与解决方法研究[J].自动化学报，2014，40（9）：1922-1932.

[10] KASSMANN D E，BADGWELL T A，HAWKINS R B. Robust steady-state target calculation for model predictive control[J]. AIChE Journal，2000，46（5）：1007-1024.

[11] 邹涛，魏峰，张小辉. 工业大系统双层结构预测控制的集中优化与分散控制策略[J]. 自动化学报，2013，39（8）：1366-1373.

[12] ZHONG Y，LUO Y. Comparative study of single-loop control and cascade control of third-order object[J]. Procedia Engineering，2011，15：783-787.

[13] 刘涛，张卫东，顾诞英. 一类开环不稳定串级控制系统的解析设计[J]. 控制与决策，2004，19（8）：872-876.

[14] 罗雄麟. 化工过程动态学[M]. 北京：中国石化出版社，2005.

[15] 俞金寿，蒋慰孙. 过程控制工程[M]. 北京：电子工业出版社，2007.

[16] 罗雄麟，叶松涛，许锋，等. 流量同时作为工艺优化变量和串级控制副变量时的工艺优化实现与分析[J]. 化工自动化及仪表，2015，42（5）：475-478.

[17] 许锋，翟炳鑫，罗雄麟. 催化裂化装置分离系统稳态优化及动态实现[J]. 计算机与应用化学，2011，28（11）：1397-1403.

[18] FINKLER T F，KAWOHL M，PIECHOTTKA U，et al. Realization of online optimizing control in an industrial polymerization reactor[C]//Proceedings of the International Symposium on Advanced Control of Chemical Processes，2012.

[19] STEINBOECK A，GRAICHEN K，KUGI A. Dynamic optimization of a slab reheating furnace with consistent approximation of control variables[J]. IEEE Transactions on Control Systems Technology，2011，19（6）：1444-1456.

[20] MARKUS K，ZHANG P，SIRKKA L. An embedded fault detection，isolation and accommodation system in a model predictive controller for an industrial benchmark process[J]. Computers and Chemical Engineering，2008，32（12）：2966-2985.

[21] 靳其兵，刘斯文，权玲，等. 基于奇异值分解的内模控制方法及在非方系统中的应用[J]. 自动化学报，2011，39（3）：354-359.

[22] 林晓钟，谢磊，苏宏业. 模型不确定条件下预测控制经济性能评估的研究[J]. 自动化学报，2013，39（7）：1141-1145.

研究开发

Implementation of model predictive control on cascade control

LUO Xionglin，YE Songtao，XU Feng，XU Jun
（Department of Automation，China University of Petroleum-Beijing，Beijing 102249，China）

Abstract：In chemical process control，the flow rate is usually set as the minor loop of cascade control for the other more important controlled variables such as temperature，liquid level and material component. At the same time，the flow rate is often the manipulated variable of model predictive control（MPC）. In view of the implementation dilemma of downloading the manipulated variable of MPC while the flow rate control is set as minor loop of cascade control，two implementation methods of MPC were proposed. Firstly，the output of MPC is downloaded to the set-point of major loop through an one order inertia object. Secondly，the transfer function of flow rate to controlled variable of major loop is embedded into the predictive model of MPC. The control of the Shell heavy oil fractionator’s benchmark problem has proved the feasibility of the two methods. They are simple in theory and easy to implement for commercial processes.

Key words：process control；model predictive control；cascade control；minor loop；flow rate

基金项目：国家重点基础研究发展计划项目（2012CB720500）。

收稿日期：2015-08-24；修改稿日期：2015-09-28。

DOI：10.16085/j.issn.1000-6613.2016.02.012

中图分类号：TQ 460.6

文献标志码：A

文章编号：1000–6613（2016）02–0417–08