一种基于Logistic混沌映射的骨干粒子群改进算法

朱雅敏， 薛鹏祥

(西安工业大学 理学院，西安 710021)



一种基于Logistic混沌映射的骨干粒子群改进算法

朱雅敏， 薛鹏祥

(西安工业大学 理学院，西安 710021)

摘要：针对骨干粒子群算法因受初始化位置分布不均影响，易陷入局部最优的问题，提出一种基于Logistic混沌映射的改进算法，改进算法通过采用Logistic混沌映射控制来保证粒子初始化位置在搜索空间内保持随机分布，从而有效提升算法的搜索能力.仿真实验表明：与经典骨干粒子群算法相比，改进算法搜索能力有所增强，问题求解精度有明显提升.

关键词：骨干粒子群;Logistic混沌映射;随机初始化

粒子群算法(Particle Swarm Optimization，PSO)是由社会心理学家James Kennedy和电子工程学专家Russell Eberhart于1995年提出的[1]，是继遗传算法之后，产生的一种全新的智能优化方法，其基本思想是通过种群中粒子间的合作与竞争产生的群体智能指导优化搜索，其原理和机制简单，既保持了进化算法深刻的群体智能背景，又有着良好的优化性能.因此，PSO算法已广泛应用到函数优化、多目标规划、神经网络训练、模糊系统控制等领域.

由于标准粒子群算法中涉及参数较多，Kennedy于2003年提出了骨干粒子群算法(Bare Bones PSO，简写为BBPSO)[2]，BBPSO算法仅仅利用关于微粒全局值和个体极值的高斯分布完成微粒位置的更新，避免了复杂的参数调节，是一种十分有潜力的PSO变形算法，但由于取消了速度变量及惯性因子等参数，故BBPSO的收敛速度与求解精度等指标仅取决于粒子初始位置的选取，粒子群位置初始化的策略会直接决定BBPSO的表现.

针对粒子位置的初始化策略，文献[2]采用的是伪随机数的方式，为了提升BBPSO的表现，后来BBPSO算法出现了许多新变种，如文献[3]中采用了高斯分布和柯西分布来完成迭代时的位置更新，文献[4]中增加了扰动的方式以实现迭代时粒子位置变化的多样性，但后续所有这些变种均沿用文献[2]的伪随机数初始化方式.本文参考混沌理论的思想，提出了一种新型的粒子初始化策略：Logistic混沌映射法，仿真测试结果表明，采用Logistic混沌映射策略会获得更好的效果.

1标准粒子群算法简介

假设搜索空间维数为D，粒子总数为N.Pi(t)=(Pi1(t),Pi2(t),…,PiD(t))表示第i个粒子经过t次飞行后的位置，Vi(t)=(Vi1,Vi2,…,ViD)表示第i个粒子第t次飞行的速度和方向，Pbest=(Pi1,Pi2,…,PiD)表示第i个粒子第t次飞行及之前整个寻优过程中的最优位置，gbest=(gi1,gi2,…,giD)表示第t次飞行及之前整个粒子群寻优过程中的最优位置.则标准粒子群算法可以由以下公式进行描述：

Pi(t+1)=Pi(t)+Vi(t+1)t=0,1,2,…

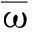
2骨干粒子群算法流程

Clerc和Kennedy分析微粒运动轨迹后，证明了标准PSO算法中，每个微粒i向它的个体历史极值和全局极值的加权平均值Gi收敛[5]，即

式中c1,j,c2,j为[0，1]区间内的随机数，当迭代次数趋于无穷时，所有微粒将收敛到同一点.

受上述思想启发，Kennedy于2003年提出了骨干粒子群算法(BBPSO)，BBPSO算法利用关于微粒全局值和个体极值的高斯分布完成微粒位置的更新：

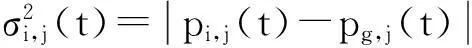
BBPSO算法的流程如下：

P0.针对具体问题，设定误差预设值或迭代最大次数.

P1.在搜索空间内，针对每个粒子，对粒子位置进行初始化(如是标准BBPSO算法，此处采用伪随机数法).

P2.根据方程[3]进行迭代.

P3.采用迭代后的粒子位置，计算函数适应度.

P4.根据计算所得函数适应度，计算误差.

P5.如误差小于预设值或迭代达到最大次数，则输出结果退出，否则转回P2.

在标准BBPSO算法中，由于后续算法固定，无其他任何参数可供调整，故算法的收敛性与精度等指标唯一取决于粒子初始化位置，故本文以粒子初始化策略作为研究对象，针对上述算法流程，对应的步骤为P1.

3初始化策略

3.1伪随机数法

目前已有的BBPSO及其变形算法初始化一般采用此法，各种语言的底层库对此实现基本相同，均采用线性同余法(LCG，LinearCongruenceGenerator)，但此法存在严重的缺陷，文献[6]中证明如采用此法初始化N维空间的点坐标，这些点最多位于m1/n超平面上，这是由于产生的X(n)值的前后强关联所致.

设搜索空间为[-S，S]，空间维度为d，则针对某一维度，粒子的位置可按照如下方式进行初始化：

pi,j=(rand()*2-1)*S

3.2Logistic混沌映射

混沌来自于非线性动力系统，描述的是任意随时间变化的过程，这个过程是确定性的、类似随机的、非周期的、具有收敛性的，并且对于初始值有极敏感的依赖性.

Logistic一维混沌映射数学形式表述简单，但具有极其复杂的动力学行为，其数学表达公式如下[7]：

xn+1=μ*xn*(1-xn)x∈[0,1]

其中μ∈[0,4]称为Logistic参数.

a)当0<μ≤1

此时该模型的状态简单，曲线迅速趋于0，且0就是吸引子，迭代方程最终归于0值不变.

b)当1<μ≤3

该模型状态比较简单，不动点0，1-1/μ为仅有的两个周期点.

c)当3<μ≤4

此时该模型状态十分复杂，系统由倍周期通向混沌.

d)当μ>4

此时该系统状态毫无混沌现象，0为唯一的吸引子.

由上可见Logistic系统随着μ增大的变化情况是：非混沌一混沌一非混沌，经研究发现，Logistic方程仅3.566 9<μ≤4时，该方程呈现混沌状态[8].

在本文中，令μ=3.999.此时有初始条件X0在Logistic映射作用下产生的序列是混沌状态、非周期的、不收敛的，故可采用此序列对粒子位置进行初始化.

本文中采用此方法的初始化方式为：

pi,j=(xi*2-1)*S

4数值仿真及分析

基于上文所述之算法，采用Python语言及其科学计算扩展包numpy、scipy编写了仿真测试程序，针对下述典型的函数进行了实际测试.

实际测试中，采用伪随机数策略初始化的算法标记为BBPSO1，采用Logistic混沌映射策略初始化的算法标注为BBPSO2.

参考文献[9]、[10]、[11]，本文最终选定下面四个典型的函数作为仿真测试函数，具体的仿真测试结果如下：

4.1Rosenbrock函数

Rosenbrock函数，非凸，病态函数，在xi=1时达到极小值0.

参数设置：粒子总数50,搜索空间[-30,30]，迭代次数100次，经过50次运行后，测试数据如表1：

表1　Rosenbrock函数极值测试结果

4.2Rastrigin函数

Rastrigin函数，多峰函数，在xi=0(i=1，…，n)时达到全局极小点，在S={xi∈(-5.12,5.12),i=1,2，…，n}范围内大概存在约10n个局部极小点.

参数设置：粒子总数50,搜索空间[-5.12,5.12]，自变量维度30，常数A取10，迭代次数100次，经过50次运行后，测试数据如表2：

表2　Rastrigin函数极值测试结果

4.3Schewelfel函数

Schewelfel函数，单峰，在xi=0时达到极小值0.

参数设置：粒子总数50,搜索空间[-30,30]，自变量维度30，迭代次数100次，经过50次运行后，测试数据如表3：

表3　Schewelfel函数极值测试结果

4.4Sphere函数

Sphere函数，单峰，在xi=0时达到极小值0.

参数设置：粒子总数50,搜索空间[-100,100]，自变量维度30，经过50次运行后，测试数据如表4：

表4　Sphere函数极值测试结果

5数值仿真及分析

根据上述仿真测试结果可知，与BBPSO1相比，BBPSO2的收敛速度、搜索精度、跳出局部最优能力都有不同程度的加强.以上仿真结果证明，不管是多峰函数还是单峰函数，采用Logistic混沌映射的骨干粒子群改进算法均具备可行性和有效性.

[1]KENNDY J，EBERHART R C.Particle swarm optimization[C].Proc IEEE Int Conf on Neural Networks，Perth，WA，Australia，1995：1942-1948.

[2]KENNEDY J.Bare bones particle swarms[C].Proceedings of the IEEE Swarm Intelligence Symposium，2003：80-87.

[3]KROHLING R A.Bare bones particle swarm optimization with gaussian or cauchy jumps，Evolutionary Computation[C].CEC′09.IEEE Congress，2009：3285-3291.

[4]MOHAMMAD M R. Bare bones particle swarms withjumps[J].Lect Notes Comput Sci.，2005， 7461:49-60.

[5]VAN DEN BERGH F，ENGELBRECHT A.A study of particle swarm optimization particle trajectories[J].Information Sciences，2005，176(8)：937-971.

[6]MARSAGLIA G,TSANG W W.The Monty Python method for generating random variables[J].ACM Transactions on Mathematical Software,1998,24 (3):341-350.

[7]GRASSBERGER P,PROCACCIA I.Measuring the strangeness of strange attractors[J].Physica D，1983，9 (1-2):189-208.

[8]SPROTT,CLINTON J.Chaos and time-series analysis[M].Oxford：Oxford University Press，2003.

[9]WILLIAM M S,DEREK T G,DIANA F S.Biases in particle swarm optimization[J].International Journal of Swarm Intelligence Research,2010，1(2):34-57.

[10]JONES D.Good practice in (pseudo) random number generation for bioinformatics applications[C].Technical report,UCL Bioinformatics Group,2010.

[11]MARINAKIS Y,MARINAKI M.A hybrid genetic-Particle Swarm Optimization Algorithm for the vehicle [J].Expert System with Applications,2010,37:1446-1455.

[责任编辑王新奇]

An Improved Algorithm for Backbone Particle Swarm OptimizationBased on Logistic Chaotic Mapping

ZHU Ya-min, XUE Peng-xiang

( School of Science, Xi’an Technological University, Xi’an 710021, China )

Abstract：In this paper, aiming at the problem that the backbone particle swarm algorithm is easy to fall into local optimum because of uneven distribution of the initial position, an improved algorithm based on logistic chaotic mapping is proposed. By using the logistic chaotic mapping control to ensure that the initial position of particles in the search space to maintain a random distribution, therefore, the search ability of the algorithm is effectively improved. The simulation experiments show that the search ability of the improved algorithm has been significantly enhanced and its problem solving accuracy is significantly improved compared with that of the classical PSO algorithm.

Key words：backbone particle swarm; Logistic chaotic mapping; random initialization

中图分类号：TP183

文献标志码：A

作者简介：朱雅敏(1977—)，女，河北保定人，西安工业大学理学院讲师，硕士，主要从事数值代数及智能算法研究.

基金项目：陕西省教育厅项目(14JK1347)

收稿日期：2015-11-02

文章编号：1008-5564(2016)01-0001-04