变电站绝缘设备水冲洗机器人结构优化设计与仿真

2016-03-18Optimizationdesignoflargearmstructureofwaterwashingrobot

制造业自动化 2016年1期

关键词：结构优化仿真

Optimization design of large arm structure of water washing robot

崔孔龙1，鲁守银1，谈金东2，李　辉3

CUI Kong-long1, LU Shou-yin1, TAN Jin-dong2, LI Hui3

（1.山东建筑大学机器人与智能系统研究院，济南 250101；2.田纳西大学电子信息工程系，田纳西 37996；3.山东建筑大学机电工程学院，济南 250101）

变电站绝缘设备水冲洗机器人结构优化设计与仿真

Optimization design of large arm structure of water washing robot

崔孔龙1，鲁守银1，谈金东2，李辉3

CUI Kong-long1, LU Shou-yin1, TAN Jin-dong2, LI Hui3

（1.山东建筑大学机器人与智能系统研究院，济南 250101；2.田纳西大学电子信息工程系，田纳西 37996；3.山东建筑大学机电工程学院，济南 250101）

摘要：为了提高变电站绝缘子的冲洗效率，对水冲洗机器人的大臂结构尺寸进行优化设计。首先，确定与冲洗效率相关的大臂结构参数，然后，根据要求确定大臂的优化函数进行结构优化，运用约束坐标轮换法求取大臂结构参数，根据实验获取的数值运用MATLAB进行仿真，画出运动轨迹。优化的结果可使大臂的末端沿近似的水平线运动，且冲洗效率大大提高。

关键词：水冲洗机器人；结构优化；冲洗效率；运动轨迹；仿真

0 引言

变电站很多电气高压设备长期运行在户外，绝缘子表面污秽比较严重，易造成停电及污秽闪络事故[1,2]，及时清理绝缘子表面的污秽变的尤为重要。目前国内大多采用人工的方式，劳动强度大，而且存在安全隐患。国外带电水冲洗绝缘设备的方式比较先进，如意大利Pisa University通过用直升机安放带电水冲洗机器人的方法进行冲洗[3]，这种方法成本太高，而且难于操作。在国家863计划的资助下，我们进行了水冲洗机器人的研究且取得良好的效果，但机械臂关节比较多，操作比较麻烦，导致冲洗过程中造成绝缘子冲洗不全面，冲洗时间长等问题。因此，为提高冲洗效率，我们简化机械臂关节数，采用枪口与绝缘子垂直、等距的水平冲洗方法。为了实现该方法及减少机械臂的关节数，我们对多种方案反复设计筛选，并最终做出了优化后的水冲洗机器人如图1所示，结构方案原理图如图2所示。

图1　水冲洗机器人实物图

图2　结构方案原理图

该结构方案的动作原理是：大臂3在油缸2的驱动下实现上升下降，以满足绝缘子的上下冲洗；支撑臂1保证大臂可以垂直起落；小臂4在液压马达6的作用下可以在水平面内做±60°的摆动，以调整小臂4前端的左右位置；液压马达7驱动枪杆5沿绝缘子的外表面进行旋转，旋转角度可达±50°；液压马达8、9驱动移动平台做前后往复运动及左右旋转。喷枪的运动轨迹如图3(a)所示。

图3　喷枪运动

因为变电所电压为220kV，所以水柱的长度至少为1000mm，而实际水柱的长度可以达到10000mm，冲洗的绝缘子直径在300mm左右，可以近似认为水柱与绝缘子表面垂直。在进行水冲洗作业时大臂与旁边绝缘子的距离应大于安全距离S，S>360mm，且大臂沿绝缘子方向的距离H2小于2000mm，否则会导致绝缘子与机械臂发生放电，以致发生危险事故。图3(b)为冲洗内部绝缘子示意图。

为了满足变电所绝缘子冲洗控制上要求，对水冲洗机器人的大臂结构设计还进行如下特殊要求：1）大臂的起落高度达5000mm；2）在到达清洗高度时，大臂的前端应近似沿一条水平线运动，其水平度绝对偏差即沿y轴方向的摆动不大10mm为宜；3）大臂在起落时，沿垂直方向起落，在z轴方向的偏差小于6mm为宜；4）冲洗内部绝缘子时，大臂与两边绝缘子的距离应大于300mm。

1 机械臂参数的优化设计

1.1 机械臂参数的确定

水冲洗机器人的机械臂为3自由度关节型，为了描述大臂的运动轨迹，以机械臂末端中心为坐标原点建立坐标系，绘制机械臂的结构简图，其中基座长度、大臂长度、小臂长度依次为L0、L1、L2；其中L1为可伸缩杆件，大臂宽度为L3，机械臂基座与Y轴正方向的夹角为θ0，大臂的旋转角度为θ1，沿y轴方向旋转，小臂的旋转角度为θ2，沿Z轴方向旋转。图4中(a)为机械臂参数化后的图形，小臂末端坐标为P(x,y,z)。

图4　机械臂参数化

小臂末端坐标P(x,y,z)，满足如下关系：

式中：

d为绝缘子的半径，在此，我们取d=200mm。

机械臂在X-Y-Z平面内的作业区域如图4(b)所示。曲线P1P2为大臂达到最大角度θ1max，小臂夹角由θ2min到θ2max变化时的曲线；曲线P3P4为大臂达到最小角度θ1min，小臂夹角由θ2max到θ2min变化时曲线[4]；交点依次为P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)、P4(x4,y4,z4)，由式(1)可求出各点：由P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)、P4(x4,y4,z4)可知，机械臂的运动坐标是AB、BC、CD、DB、H1、L1、L2的函数，同时考虑到冲洗中间绝缘子时的一些限制因素L3、H2，它们是需要优化设计的变量，现用W表示则有：

1.2 建立目标函数

根据设计要求，我们期望的函数应该[5]是：

式(3)期望在进行冲洗作业时大臂末端沿水平线移动，上下浮动尽量小；式(4)期望大臂可以垂直起落，在进行上下清洗时可以垂直进行；式(5)期望大臂末端的起落高度为5000mm。

为了使大臂末端的运动满足上述函数的要求，求出各分点输出的F(yi) (i=1,2,…,n)对平均值的偏差；大臂抬起时的水平分点F(zi) (i=1,2,…,n)对均值得偏差；大臂末端的起落高度对5000mm的偏差；为保证机械臂结构的紧凑性使AB、BC、CD、L2的总和最小，为满足上面四部分的权重要求我们引进加权因子λ1、λ2、λ3和λ4，建立如下的目标函数：式中F(yi) (i=1,2,…,n)为进行水冲洗作业时，大臂末端各分点处实际的y坐标值，为轨迹上各分点的y坐标的平均值；Yn为进行水冲洗作业时大臂的最大高度值，Y1为最小高度值；F(zi) (i=1,2…,n)为大臂起落时各点的实际的z坐标，为水平轨迹上z坐标的平均值；λ1、λ2、λ3和λ4分别为小于1的加权因子，且λ1+λ2+λ3+λ4=1。

1.3 确立约束条件

因为各变量不能为负值，故可以确定如下的约束条件：

为保证油缸构成的三角形结构，应满足：

为限制B点移动范围，我们进行以下设定：

当冲洗绝缘子的底端时，为保证稳定性大臂不能太长，因此：

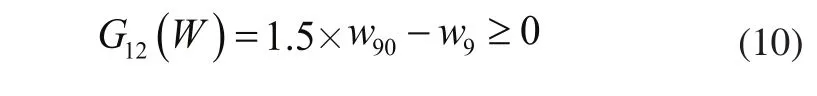
其中，w90为大臂初始长度。

为避免在冲洗过程中绝缘子对机械臂放电，因此：

将目标函数与前述的约束条件联立起来就构成了优化设计数学模型。

1.4 优化方法及最终结果

本论文中，我们运用约束坐标轮换法[6,7]对未知数进行求解，用VBS进行编程，其求解流程图如图5所示。

图5　编程流程图

式中，h=0.5，ε==00.2.2。因未知数的个数小于10个，故约束坐标轮换法可以快速的求解出最优的结果。

对于加权因子的选择，我们采用先选取再通过实际数据检验调整的方法，进行大量的实验计算，最终选定比较合适的四个值分别为：1=0.05、2=0.80、3=0.05、4=0.10将1、2、3、4带入优化函数通过程序的多次运算，最后选择了一组最满意的结果，如表1所示。

表1　运算结果(单位：mm)

通过MATLAB的SimMechanics模块编写程序对上述求解结果进行验证，对仿真后的点进行记录，绘制水冲洗机器人机械臂末端的运动轨迹，图6(a)为大臂末端移动轨迹。通过运动轨迹我们可以发现：1）机械臂的运动满足与绝缘子表面垂直等距的关系；2）大臂的起落高度满足水冲洗的需求，大约维持在5000mm；3）在进行冲洗作业时，末端基本沿水平线移动，其偏差在10mm以内。机械臂的设计满足快速冲洗绝缘子的要求。图6(b)、图6(c)为对内部绝缘子进行冲洗的仿真图。我们可以发现机械臂可以对内部绝缘子进行充分的冲洗且机械臂有效的避开了绝缘子的放电距离，保证冲洗作业的安全进行。