CZT和ZFFT频谱细化性能分析及FPGA实现
2016-03-17张远安张开生
马 可,张远安,张开生
(西安电子工程研究所,西安 710100)
CZT和ZFFT频谱细化性能分析及FPGA实现
马可,张远安,张开生
(西安电子工程研究所,西安710100)
摘要:快速傅里叶变换在信号的频谱分析中应用广泛,而在工程实际中往往只对信号频谱中一段区间感兴趣,需要对频谱进行细化分析;常用的频谱细化方法有线性调频Z变换(Chirp-Z Transform, CZT)算法和基于复调制的细化(Zoom-FFT, ZFFT)算法,在给出了两种频谱细化方法的计算流程后,通过MATLAB仿真说明两种算法都能提高信号频率的测量精度,最后给出了这两种算法在FPGA具体工程实现中的实现步骤。
关键词:线性调频Z变换;复调制细化;频谱细化
0引言
在信号处理中,经常需要分析信号的频谱,传统的频谱分析方法一般采用快速傅里叶变换(fast fourier transform, FFT)算法,FFT算法得到的是整个采样频率上的粗略的“全景频谱”,而在实际的应用中,往往只需要对感兴趣的某一段频谱区间进行细微观察和分析,这就需要提高所选区间的频率分辨率[1]。
频率分辨率表示频谱中能够分辨的两个频率分量的最小间隔[2],用频率间隔△f来表示。而频率间隔等于采用频率fs除以采样点数N。为了提高频率分辨率,可以采用的方法:一是降低采样频率,这会使频率分析范围缩小,并且采样频率还受采样定律限制,不可能太小;二是增加分析的采样点数,这意味着计算机的存储量和计算量大大增加,由于实际系统软件、硬件方面的限制,这样做在工程实践中并不总是可能的。
为了对窄带频谱区间进行细致观察,提出了频谱细化的概念,其基本思路就是对信号频谱中需要分析的频段进行局部放大,也即在某一频率附近局部增加谱线密度,实现选带分析。常用的频谱细化方法有线性调频Z变换(Chirp-Z Transform, CZT)算法和基于复调制的细化(Zoom-FFT, ZFFT)算法。文献[3-6]中都介绍了这两种算法的原理和性能,不过对于ZFFT算法的具体现场可编程门阵列(field programmable gate array, FPGA)实现,并没有太多介绍。本文首先简单介绍这两种算法原理并对比分析它们的性能,然后给出了这两种算法在FPGA中的具体实现步骤。
1算法分析
1.1CZT算法
CZT可以对感兴趣的某一段频谱区间进行细化,它通过对单位圆上任意一段曲线上的Z变换进行计算。对有限长序列x(n)做CZT,主要是确定需要细化频谱区间的起始频率、细化频率间隔以及取样点数,其线性滤波计算步骤如图1所示[7-8]。
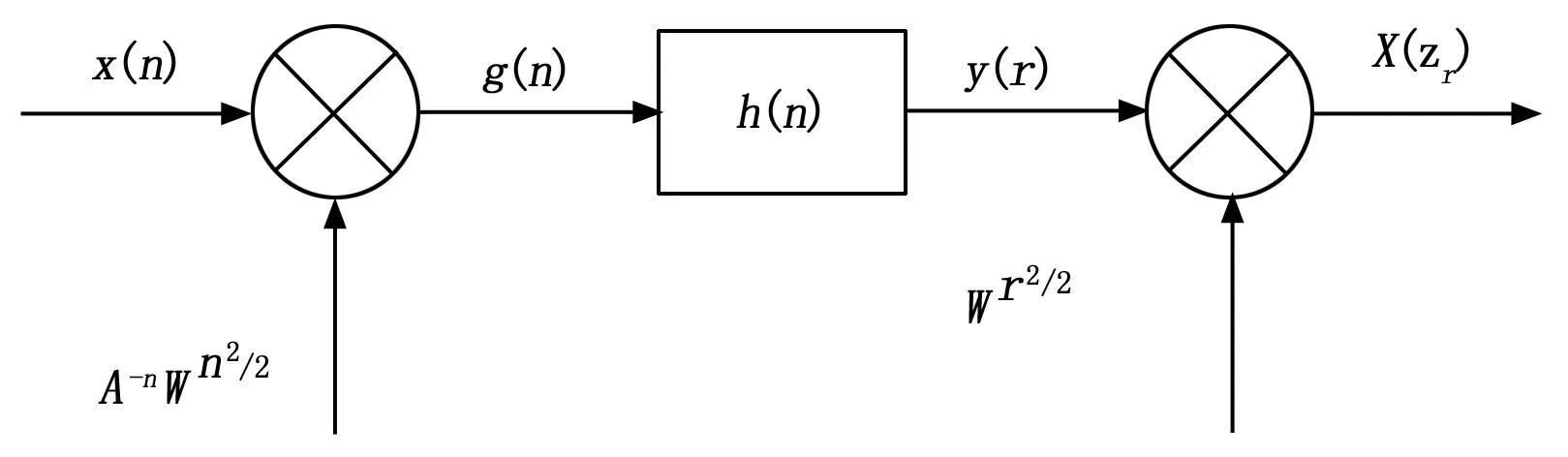
图1 CZT的线性滤波计算步骤
对于长度为M的有限长序列x(n)的CZT是:
(1)
其中:θ0为初始幅角,φ0为单位圆等间隔增量。当A0=W0=1时,即在单位圆上进行采样时,式(2)变为:
(2)
式中,θ0=2πf0/fs,φ0=2πfL/(Mfs),其中f0为分析频谱的起始频率,fL为分析频谱的长度,fs为采样频率。这样,CZT算法频率分辨率为△f=fL/M。
1.2ZFFT算法
ZFFT算法通过指定的采样频率分析整个频谱上感兴趣的一段区间。对有限长序列x(n)进行ZFFT,主要需要确定需要细化频带的频率中心fe,细化倍数D,其主要的运算流程如图2所示[9]。

图2 ZFFT运算流程
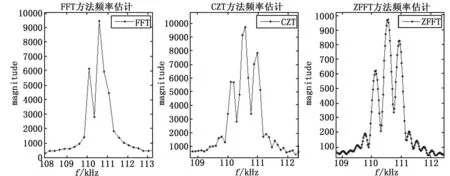
图4 多频率下的仿真结果
在确定了细化频带的中心频率fe、细化倍数D以及采样频率fs之后,就可以确定细化频带的下限频率fl=fe-fs/(2D)以及上限频率fh=fe+fs/(2D)。重采样之后如果进行N点FFT处理,则频率分辨率为△f=fs/(DN)。FFT处理之后,对结果进行频率翻转,得到最后的处理结果。
2CZT和ZFFT频谱仿真
针对上述CZT算法和ZFFT算法,我们进行计算机仿真。在仿真分析CZT和ZFFT算法对信号频谱的细化情况时,先分析单频率成分的测量精度,再分析多频率成分的测量精度。
本文仿真中,假定信号频率f为110.55 kHz,采样频率fs为500 kHz,信号幅度A=4,噪声为服从正态分布的随机噪声,方差为1.6,信噪比SNR为10 dB。用CZT算法进行分析时,细化的频率区间也设定为85 kHz~135 kHz,细化点数为512。用ZFFT算法分析时,细化频谱区间的中心频率fe为110 kHz,细化倍数D=10,则细化的频率区间也为85 kHz~135 kHz。用功率加权求平均的方法进行频谱校正,做100次Monte Carlo实验得到仿真结果如图3所示。
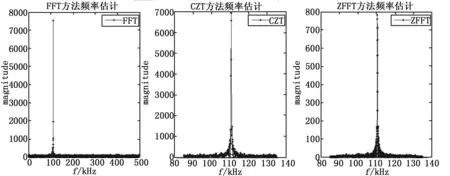
(a) 3种算法频谱分析图
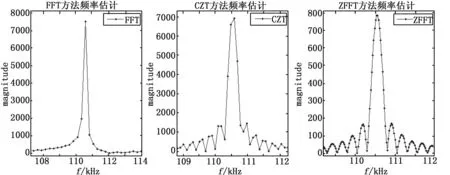
(b) 3种算法频谱分析局部放大图图3 仿真结果图
由图3可以得出,FFT方法仿真估计出的结果fFFT=110.60 kHz,误差σFFT=0.05 kHz;CZT方法仿真估计出的结果fCZT=110.59 kHz,误差σCZT=0.04 kHz;ZFFT方法仿真估计出的结果fZFFT=110.56 kHz,误差σZFFT=0.01 kHz。从图3的仿真结果可以看出,CZT算法和ZFFT算法比传统的FFT算法在频谱测量精度上,要提高很多。
除了分析单频信号,这里假设一个多频率成分的信号,频率分别为110.16 kHz,110.55 kHz,110.93 kHz,幅度分别为3,5,4,其他参数同上面仿真设计,其频谱细化的仿真结果如图4所示。
从图4中可以看到,在多频率成分时,当信号的多个频率成分很接近,FFT算法无法区分信号的3个频率,而CZT以及ZFFT算法可以区分3个频率成分的谱峰,具体的测量结果如下表1所示。
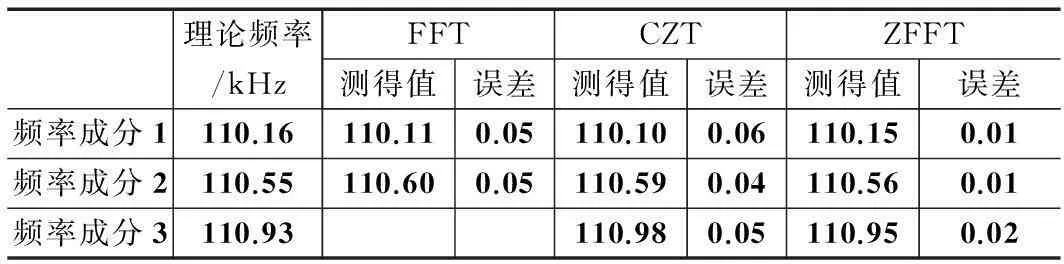
表1 3种算法频谱谱峰测量值
从仿真中可以看到,ZFFT算法在频谱细化中,比FFT算法和CZT算法精度要高很多。从频率分辨率上分析,FFT算法的频率分辨率△fFFT=fs/N=0.24 kHz,CZT算法的频率分辨率△fCZT=50/M=0.10 kHz,ZFFT算法的频率分辨率△fZFFT=fs/(ND)=0.02 kHz。所以从这一点上也可以看出ZFFT算法的频率分辨率要高些。
3CZT和ZFFT的FPGA实现
图1中介绍了CZT算法的流程,其中比较复杂的计算步骤是y(n)和h(n)的卷积,在FPGA中具体实现CZT算法时,常采用图5中的计算过程。
实现时,首先利用MATLAB产生图5中三组系数的coe文件,通过设定所需分析频谱的起始频率和分析频段的长度,细化点数,产生三组浮点型的系数,换算成16 bit的整型有符号数,存入Xilinx的Block RAM IP核中。运算时,通过设计FPGA内部程序,使得系数1读出时,与输入信号x(n)对齐,调用复数乘法器IP核进行运算,对输出结果y’(n)调用FFT
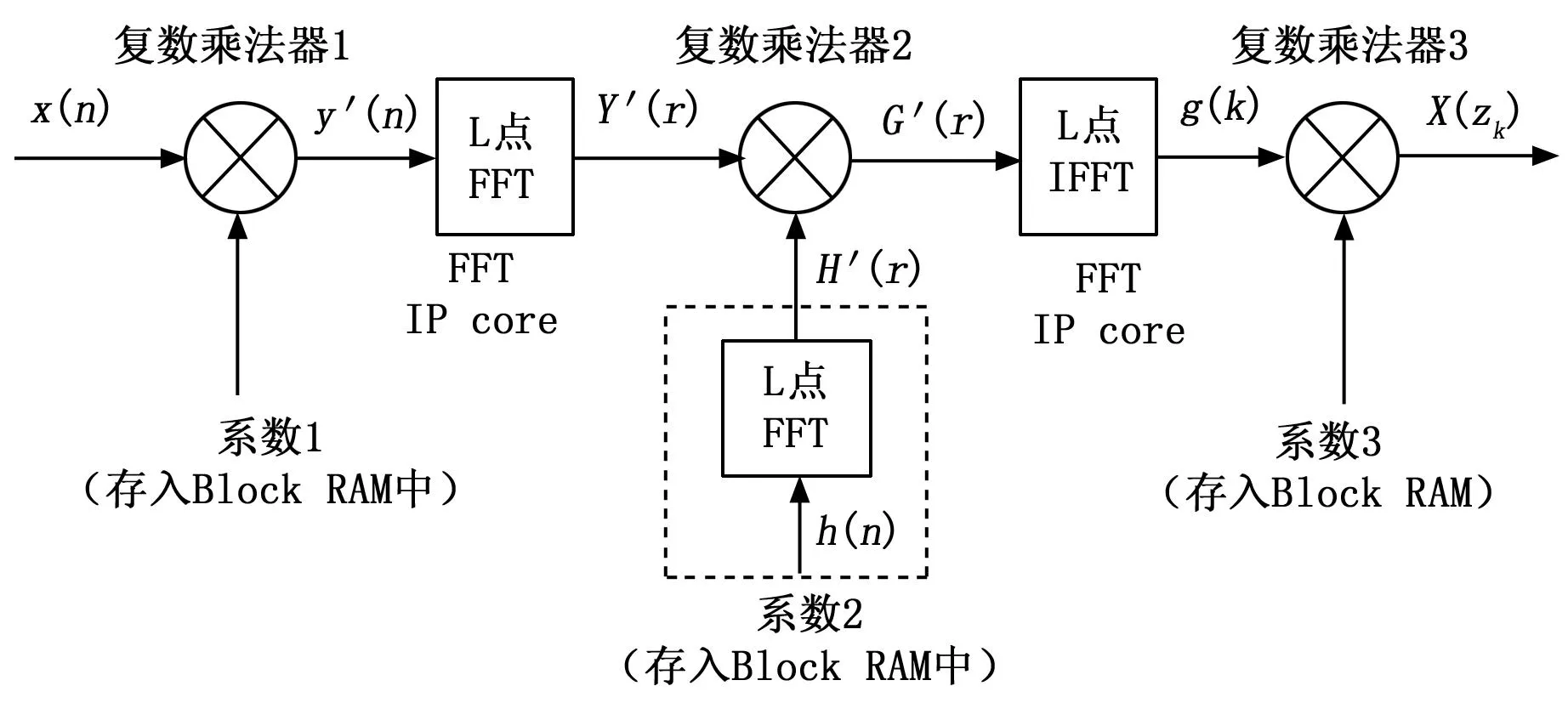
图5 CZT算法具体实现流程
运算的IP核对其进行FFT运算,结果同系数2进行复数乘法,对该结果G’(r)进行IFFT运算,其结果同系数3进行复数乘法,截取该结果的前面M点。由于FPGA内部运算时,信号位数会增加,考虑资源的情况,必须对结果进行截位。所以在设计中,必须对每一步计算结果的信号进行截位以及时序的对齐。
对于图2中ZFFT的计算过程,在FPGA中实现时,具体的流程如图6所示。

图6 ZFFT算法具体实现流程
对于ZFFT算法的实现过程,主要也是将相应的系数存入Block RAM中,实现过程中也调用的FPGA IP核中自带的运算算法,在频率调整时,由于在MATLAB中采用fftshift函数对频谱进行翻转,而在FPGA中,可以通过把FFT后的数据存入Block RAM中,然后读取时,先读取后半部分的数据,再读取前半部分的数据来实现。对于这些设计方法,在FPGA中实现起来都比较简单、方便。而且FPGA运算速度高,也能很好地满足工程需求。
4结束语
本文主要比较分析了CZT算法和ZFFT算法在频谱细化中的性能,通过MATLAB仿真分析得到这两种算法在频谱细化性能中相比较传统的FFT算法有很大的提高,并且ZFFT算法性能也稍优于CZT算法,最后给出了在FPGA中实现这两种算法的具体步骤。这种实现方法已经在工程上得到一定应用[9-10]。
参考文献:
[1] 李天昀, 葛临东. 两种快速频域细化分析方法的研究[J]. 系统工程与电子技术, 2004, 26(9): 1192-1194.
[2] 胡广书. 数字信号处理理论算法与实现[M]. 北京: 清华大学出版社, 2003.
[3] 丁康, 潘成灏, 李巍华. ZFFT与Chirp-Z变换细化选带的频谱分析对比[J]. 振动与冲击, 2006, 25(6): 9-12.
[4] 谢明, 丁康. 基于复解析带通滤波器的复调制细化谱分析的算法研究[J]. 振动工程学报, 2002, 15(4): 479-483.
[5] 王力, 张冰, 徐伟. 基于MATLAB复调制ZOOM-FFT算法的分析与实现[J]. 舰船电子工程, 2006, 26(4): 119-121.
[6] 赵宏强. 频谱细化算法分析[J]. 四川兵工学报, 2013, 34(5): 105-109.
[7] 张军团, 程德福, 林君. 储油罐液位监测雷达设计与实现[J]. 计算机测量与控制, 2004, 12(11): 1040-1042.
[8] 张红, 王晓红, 郭昕. 提高线性调频连续波雷达测距精度的ZFFT算法[J]. 航天电子对抗, 2006, 22(1): 48-51.
[9] 王向辉, 高天德, 郭秀焱,等. 基于LabVIEW的吸声系数测试系统设计[J]. 计算机测量与控制, 2011, 19(5): 1014-1016.
[10] 马可, 来晋峰, 李慧敏,等. CZT在双频连续波雷达信号处理中的应用分析[J]. 火控雷达技术, 2014, 43(3): 46-49.
Performance Analysis for CZT and ZFFT Spectrum Zoom and Its FPGA Realization
Ma Ke, Zhang Yuanan, Zhang Kaisheng
(Xi’an Electronic Engineering Research Institute, Xi’an710100,China)
Abstract:Fast Fourier Transform is widely used in the signal spectrum analysis. However, it usually gets interesting in a part of the whole signal spectrum in engineering, so it needs spectrum zoom analysis. It is the common method for spectrum zoom which including complex modulation Zoom-FFT (ZFFT) and Chirp-Z Transform (CZT). After the calculating methods of two kinds spectrum zoom are given, both ZFFT and CZT can improve the measurement accuracy by simulation in MATLAB. Lastly, this paper gives the realization steps of the two methods in FPGA engineering.
Keywords:Chirp-Z transform; zoom-FFT; spectrum zoom
文章编号:1671-4598(2016)02-0288-02
DOI:10.16526/j.cnki.11-4762/tp.2016.02.079
中图分类号:TN911.7
文献标识码:A
作者简介:马可(1988-)男,陕西西安人,工程师,主要从事雷达总体工程与雷达信号处理方向的研究。
基金项目:武器装备预先研究基金资助项目(40405040201)。
收稿日期:2015-09-08;修回日期:2015-09-29。
