基于改进确定性采样滤波的疲劳裂纹扩展RUL预测
2016-03-17李文峰许爱强张怀远
李文峰,许爱强,王 丰,张怀远
(1.海军航空工程学院 科研部, 山东 烟台 264001; 2.92635部队, 山东 青岛 266000;3.91206 部队, 山东 青岛 266000; 4.91359部队, 北京 102443)
基于改进确定性采样滤波的疲劳裂纹扩展RUL预测
李文峰1,2,许爱强1,王丰3,张怀远4
(1.海军航空工程学院 科研部, 山东 烟台264001; 2.92635部队, 山东 青岛266000;3.91206 部队, 山东 青岛266000; 4.91359部队, 北京102443)
摘要:针对确定性采样滤波在进行状态估计预测时随维数增加时出现计算量增加且精度不高的问题,提出一种确定性采样滤波的算法并将其应用到疲劳裂纹扩展RUL预测当中去;首先,阐述了确定性采样滤波的基本原理;其次,从多维数值积分的角度分析确定性采样滤波所需计算的数学期望,根据完全对称积分公式计算积分节点值、节点个数和权重;最后,将改进后的确定性采样滤波器应用到构件疲劳裂纹损伤扩展中去,并与无迹卡尔曼滤波算法、容积卡尔曼滤波算法进行比较,提升了裂纹扩展RUL预测的精度,实例仿真分析验证了该方法的可行性和有效性。
关键词:确定采样型滤波器;疲劳裂纹扩展;多维数值积分;剩余使用寿命预测
0引言
由于扩展卡尔曼滤波(EKF)方法存在需要求解雅可比矩阵、数值稳定性较差和滤波精度不高等明显缺点,已经不能满足非线性系统的滤波要求。近年来,随着对非线性系统统计滤波领域研究的日益深入,相关专家学者提出了无迹卡尔曼滤波(UKF)、高斯厄米特滤波(GHF)和容积卡尔曼滤波(CKF)等确定采样性滤波方法。这些滤波器都是以确定的数学解析式完成采样,统一称为确定性采样滤波器或确定采样型滤波器[1-4](deterministic sampling filter, DSF),不同的确定性采样滤波方法区别在对滤波方法中均值和方差的计算,其中UKF采用的是UT变换方法[5],GHF采用的是Gauss-Hermit积分方法计算采样点[6],CKF采用的是球面容积法则[7]。确定性采样滤波方法的提出,奠定了其在信号处理、金融、导航和估计预测等领域应用的理论基础。确定采样性滤波方法在保证滤波精度的同时,需要大量的计算,这在实际应用时比较困难。
本文针对确定采样型滤波器中存在的问题,对确定采样型滤波器改进计算的基础上,在至少不增加计算量的同时,提升确定采样滤波器的估计精度。同时,结构疲劳损伤扩展受环境、材料等多种参数的不确定性影响,本身是一个随机过程,利用滤波对疲劳裂纹扩展进行预测,非线性滤波方法进行疲劳裂纹扩展预测时可以消除这种不确定性。因此,针对构件疲劳裂纹扩展预测的特点,本文将改进后的确定采样型滤波器应用于构件疲劳裂纹扩展剩余使用寿命(remaining useful life,RUL)预测中。
1确定性采样滤波方法基本原理
确定采样性滤波方法是基于线性最小方差估计框架,利用系统状态的一阶矩和二阶矩(均值和方差),依据不同的方法,确定状态先验概率的均值和方差构造的采样点及相对应的权值,利用采样点对状态非线性函数的均值和方差进行近似估计。不同的确定采样性滤波方法区别在对滤波方法中均值和方差的计算。
通常,确定采样性滤波多假设状态后验分布为高斯型。
对于非线性系统
(1)
其中:xk和zk分别为状态变量和量测向量,fk(xk)和hk(xk)为已知函数,wk和vk分别为随机系统噪声和随机量测噪声,且相互独立。

(2)
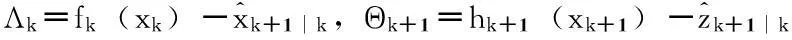
对于式(2),无法直接求解,只能通过一些数值算法近似计算,确定采样性滤波方法的估计精度取决于公式(2)的计算精度,通过不同的数值近似方法计算公式(2)将衍生出不同的滤波方法。下面通过利用数值积分容积方法,推导出相应的确定采样性滤波方法。
2基于完全对称积分公式的多维数值积分
对确定的非线性函数y=f(x),假设p(x)为x的概率密度函数,则式(2)需计算积分
(3)
若用函数g(x) 表示被积函数的其他部分,则计算其数学期望:
(4)
对公式(4),其积分的计算精度与选取的积分点有关。计算出该积分,即可计算出随机变量的均值和方差,从而完成对结果分布的高斯近似。
通常解决实际问题时,遇到的是多维随机变量x1,…,xn,其函数g(x1,…,xn)的数学期望为:
(5)
利用数值积分方法获得式(5)的近似解。数值积分的计算公式为:
(6)
其中:σj和ωj分别表示积分节点和权值,与滤波理论中的采样点和权值相对应。
确定节点个数、节点和权值,才能用Q[g]近似I[g]。节点个数的多少对计算量的大小会产生比较大的影响。节点个数越少,计算量就越小。在节点个数相同的情况下,选取不同的节点和权值,积分精度也会有较大的不同。
为了计算公式(5),相关专家学者作了大量的研究。利用高斯厄米特数值积分方法,选取高斯点和相应权值,提高系统状态的均值和方差估计的精度,诞生了高斯厄米特滤波方法[6]。但是,在高维情况下,该方法的计算负荷将呈指数增长。McNamee和Stenger定义了完全对称积分公式[8],通过求解非线性方程组的方法来得到采样点。该方法的计算负荷远小于高斯厄米特数值积分方法的计算负荷。
完全对称积分区域包括无穷区域Rn和有界区域如超球体和超球面。
对积分(5),其积分区域为完全对称,如果随机变量之间为独立同分布,那么权值函数也是全对称的,以生成元[9]的方式表示式(6),其完全对称积分公式:
(7)
若代数精度为d=2s-1,则其完全对称积分公式,所需要的最少节点个数为:
(8)
完全对称积分公式[2]的特点为:
1)完全对称积分公式能够准确积分任何包含奇次幂的单项式,如果g(x)在某个方向上含有奇次幂项,那么I=0。
2)如果g(x)只包含偶次幂项,那么积分的结果与生成元中元素的排列无关。因此,建立完全对称积分公式的精度为d=2k+1,只需要使积分公式对如下单项式能准确成立:
(9)
即
(10)
针对相应的精度,生成元的选取与单项式相关。生成元中非零元素的个数与单项式中阶次非零的变量个数相等。
当d≥5时,会出现多个变量的单项式,此时选取的生成元组合会出现不同的情况。对d=5时的生成元为[0],[u]1=[(u1,0,…,0)],[u]2=[(u2,u2,0,…,0)],根据式(8)积分节点个数为n2+n+1,根据式(10)有:
(11)
当随机变量服从标准正态分布时,I0=I2=I2,2=1,I4=3。据式(11),有
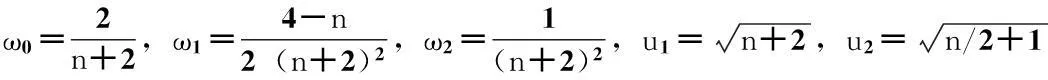
(12)
3实例仿真分析
采用完全对称积分公式对多维数值积分的积分节点的采样策略进行改进后,给出基于改进确定性采样滤波(IDSF)的剩余使用寿命预测步骤:
步骤1:在建立状态空间模型时,最佳途径是能够通过设备或部件的故障机理建立物理损伤数学模型,对于复杂的故障机理不能建立数学模型时,可根据已知的状态退化数据,根据ARMA模型、Gamma过程、HMM模型等数学统计模型描述部件的退化过程。

经状态方程中非线性函数fk(·)将ξi,k传递为γi,k+1|k,即γi,k+1|k=fk(ξi,k)。
(13)
(14)
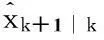
(15)
(16)
(17)
步骤5:给定新的量测信息后,执行步骤3、4,将计算结果代入贝叶斯估计框架下所需的5个数学期望进行滤波更新,得到下一时刻的状态估计。
步骤6:在状态估计的基础上,执行后期的计算处理,实现剩余使用寿命预测,并给出预测结果的概率密度分布。
给定基于改进确定性采样滤波的预测方法、步骤后,在实例仿真分析中,主要从数据准备、状态估计、评价指标以及RUL预测4个方面实现改进求积公式的确定性采样滤波RUL预测,选用应用较广泛的UKF及近年来新提出并逐渐成为研究热点的CKF与本文所提的IDSF进行仿真比较。
3.1数据准备
(18)
(19)
其中:ω1(t)为高斯噪声,均值为0.045,标准差为0.116;ω2(t)为零均值高斯噪声,标准差为0.01,初始协方差矩阵P0|0=[0.10;00.1]。其他参数参照文献[10-11]。
量测方程为:
(20)
其中:量测噪声ν(t)为零均值高斯噪声,标准差为0.074。
3.2状态估计
结构疲劳损伤扩展受环境、材料等多种参数的不确定性影响,本身是一个随机过程,利用滤波对疲劳裂纹扩展进行预测,后期得到的概率密度函数表达了这种不确定性。仿真时间100个载荷循环周期,在相同初始条件下采用CKF、UKF、IDSF分别进行了仿真,仿真结果如图1所示。
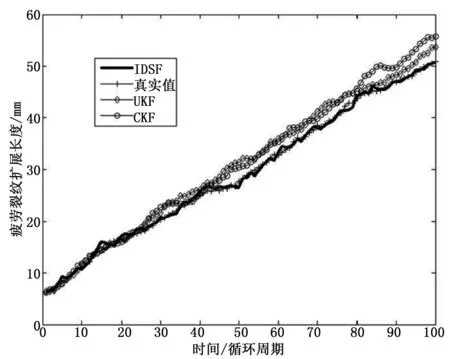

图1基于UKF、CKF以及IDSF的疲劳裂纹扩展状态估计
从图1状态估计曲线可以看出,UKF和CKF在48个循环周期后对真实状态的跟踪性能变差,但UKF的性能在第80个循环周期后稍优于CKF,这是因为当系统状态维数不大于3时,UKF相比CKF,更适合解决非线性状态估计问题;当系统状态维数达到20以上时,UKF因参数选择经常出现滤波发散的问题,相比UKF,CKF在采样和滤波过程中,不需要进行参数的选择计算且不受状态维数高低的影响,权值始终保持为正值,算法应用范围较广。但是从仿真分析来看,UKF和CKF都不如本文提出的IDSF。
3.3评价指标
采用平均相对误差作为估计预测评价指标,公式为:
(21)
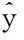
表1对比了UKF、CKF以及本文提出的IDSF方在进行疲劳裂纹扩展RUL预测时的仿真时间和平均相对误差,从表1中可以看出,从起始裂纹长度为6.93 mm开始,本文提出的IDSF方法的仿真时间大于CKF的仿真时间,而小于UKF的仿真时间,这说明UKF的计算复杂度要高于IDSF和CKF,在平均相对误差方面,UKF的平均相对误差稍小于CKF的平均相对误差,而本文提出的IDSF方法平均相对误差要小于UKF和CKF二者,这说明将3种方法用于疲劳裂纹扩展RUL预测中当属本文提出的IDSF方法精度最高。
表1 3种方法的仿真时间和平均相对误差
3.4RUL预测
上述分析可以看出,IDSF在进行疲劳裂纹扩展状态估计时,估计精度优于UKF和CKF,因此选择本文方法进行疲劳裂纹扩展预测,在疲劳裂纹扩展状态估计的基础上,对数据做后期进一步处理,在此过程中,IDSF滤波消除了剩余使用寿命中的不确定性,从图2中可以看出,在给定疲劳裂纹扩展长度失效阈值为40mm后,确定了RUL预测的预测区间,同时给出了预测结果的概率密度分布,从图2中可以得到,以疲劳裂纹长度为6.93 mm为当前起始点,则疲劳裂纹扩展的剩余使用寿命为83个循环周期通过计算,疲劳裂纹扩展的预测区间为[70,100],置信度为90%。
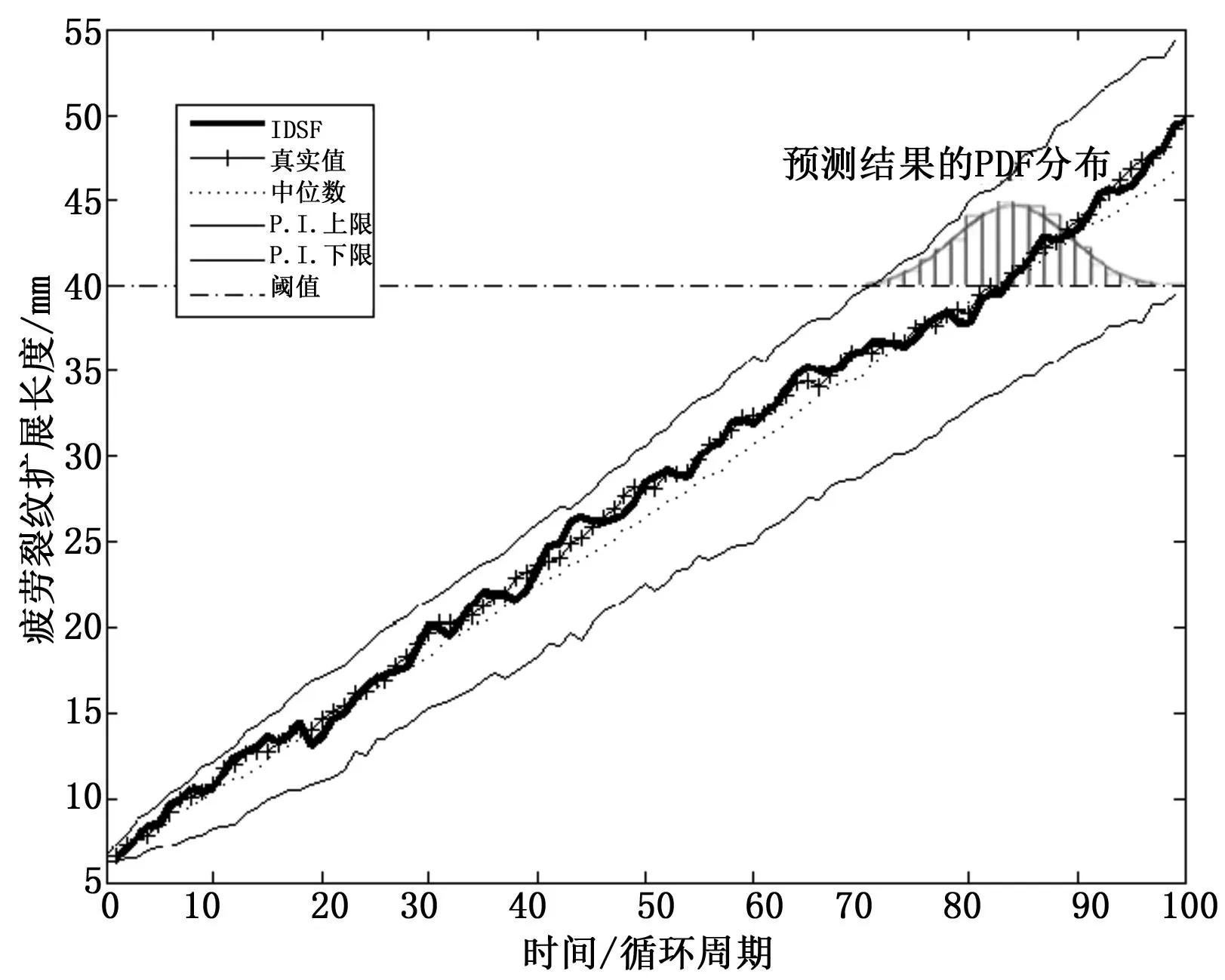
图2 疲劳裂纹扩展的IDSF剩余使用寿命预测
4结论
本文针对确定性采样滤波所需计算的数学期望,采用多维数值积分求积公式近似求取数学期望,采用完全对称积分公式求取积分节点的位置、个数和权重,改进采样节点的选取策略,提高剩余使用寿命预测的精度,通过疲劳裂纹扩展的算法仿真对比,本文提出的IDSF方法精度高于UKF和CKF,验证了该方法的有效性和可行性。
参考文献:
[1] 刘伟, 杨峰, 张洪才,等. 状态估计中确定性采样滤波器的比较分析[J]. 系统仿真学报, 2007, 19(18): 4265-4269.
[2] 丛源林,李文峰,王丰.基于多维数值积分的高阶确定采样型滤波方法[J]. 海军航空工程学院学报, 2014, 29(6): 547-551.
[3] 王小旭, 潘泉, 黄鹤,等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策. 2012, 27(6): 801-812.
[4] 刘涛, 解永春. 一种自适应确定性采样滤波方法[J]. 信息与控制, 2010, 39(6): 673-680.
[5] 张勇刚,黄玉龙,武哲民,等.一种高阶无迹卡尔曼滤方法[J]. 自动化学报,2014, 40(5): 838-847.
[6] Ito K, Xiong K. Gaussian filters for nonlinear filtering problems[J]. IEEE Transactions on Automatic Control, 2000, 45(5): 910-927.
[7] Arasaratnam I, Haykin S. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.
[8] McNamee J, Stenger F. Construction of fully symmetric numerical integration formulas[J]. Numer. Math., 1967(10):327-344.
[9] Stroud A H. Secrest D. Approximate integration formulas for certain spherically symmetric regions[J]. Math. Comput., 1963,17:105-135.
[10] Baraldi P, Compare M, Sauco S, et al. Ensemble neural network-based particle filtering for prognostics[J]. Mechanical System and Signal Processing, 2013, 41: 288-300.
[11] 袁慎芳, 张华, 邱雷,等. 基于粒子滤波算法的疲劳裂纹扩展预测方法[J]. 航空学报, 2013, 34(12): 2740-2747.
Research on RUL Prediction of Improved Deterministic Sampling Filter for Fatigue Crack Propagation
Li Wenfeng1,2, Xu Aiqiang1, Wang Feng3, Zhang Huaiyuan4
(1.Department of Scientific Research, Naval Aeronautical and Astronautical University, Yantai264001,China; 2.92635 Troop, Qingdao266000,China; 3.91206 Troop, Qingdao266000,China; 4.91359 Troop, Beijing102443,China)
Abstract:In view of the problem of increasing the accuracy of the computation of the deterministic sampling filter in the state estimation, a new algorithm is proposed and applied to the prediction of fatigue crack growth. First of all, the basic principle of determining the sampling filter is described. Secondly, from the point of view of multidimensional numerical integration, the mathematical expectation of deterministic sampling filter is analyzed, and the integral node value, the number of nodes and the weights are calculated according to the fully symmetrical integral formula. Finally, the improved model is applied to the fatigue crack propagation of the members, and the accuracy of the crack propagation prediction is improved by comparing with unscented Kalman filtering algorithm and cubature Kalman filtering algorithm. The feasibility and effectiveness of the proposed method are verified by simulation analysis.
Keywords:deterministic sampling filter; fatigue crack propagation; multidimensional numerical integration; remaining useful life prediction
文章编号:1671-4598(2016)02-0205-04
DOI:10.16526/j.cnki.11-4762/tp.2016.02.057
中图分类号:TP273
文献标识码:A
作者简介:李文峰(1983-),男,山东荣成人,博士生,主要从事航空装备故障预测与综合保障研究。许爱强(1964-),男,山东即墨人,教授,博士生导师,主要从事自动测试与装备综合保障研究。
基金项目:总装武器装备预研基金(9140A27020214JB14436)。
收稿日期:2015-08-16;修回日期:2015-09-17。
