基于Systolic阵的IQRD-SMI算法的研究与FPGA优化实现

刘禹韬，包志强，李龙龙，苏子昊

(西安邮电大学，西安　710061)



基于Systolic阵的IQRD-SMI算法的研究与FPGA优化实现

刘禹韬，包志强，李龙龙，苏子昊

(西安邮电大学，西安710061)

摘要：针对自适应波束形成系统中权值求解计算量大的问题，研究了基于LCMV的逆QR分解算法(IQRD-SMI算法) 及其传统脉动流水的GR-TSA实现结构，在Matlab中对算法以脉动阵搭建并进行算法仿真；分析了CORDIC技术的原理以及如何利用它在FPGA上实现Systolic阵中的处理单元；在此基础上，给出一种基于Systolic阵列的复用IQRD-SMI算法实现结构GR-ITSA，比较了它与已有文献中结构的异同；基于ISE软件，在Xilinx的xc7k325t型FPGA上实现了基于脉动阵列的IQRD-SMI算法的底层设计和硬件仿真，并将FPGA定点仿真数据回传Matlab与计算机浮点仿真数据对比，进而进行系统的性能与误差分析。

关键词:自适应波束形成算法；FPGA；Matlab；脉动阵；CORDIC技术；GR-ITSA

0引言

自适应数字波束形成(ADBF)系统中，为了改善波束性能、增强期望信号的信噪比，应使用高效的自适应算法对即时采样数据进行处理[1-3]。但自适应算法运算量庞大、并行与实时性能差、硬件实现资源消耗大的问题在实际应用中比较突出[4-6]。

为应对以上问题，Teitelbaum[7]提出了对采样协方差矩阵直接进行QR分解的 (QRD-SMI)算法，该算法具有高度并行性结构，易于使用Systolic脉动阵列搭建，在实际应用中能够与高性能的FPGA结合实现[8-9]。但是传统的QRD-SMI算法存在需要通过求解两个三角矩阵才能得到加权矢量w的缺点，并且后向带入需用到资源消耗很高的硬件除法器，这对于系统的实现和权矢量w的实时并行获取增加了复杂度。文献[10]中对此算法进行了详细的介绍。

文献[11]提出了一种逆QR分解算法(IQRD-SMI)，该算法避免了通过前向带入和后向带入的方式求解方程，在脉动阵结构上的优化达到了可以实时、并行地进行权值获取，更易于硬件实现。但是并没有实际的工程实现，并且其结构在具体实现中存在软件编程复杂和硬件资源消耗高的问题。

本文研究了数字逆QR分解SMI波束形成算法，结合Systolic阵在Matlab中搭建仿真实验，介绍了CORDIC算法与使用方法，并用Verilog语言在ISE中进行了硬件实现，进一步提出了一种复用的硬件实现结构GR-ITSA，简化了软件编程，节约了硬件资源成本。并将硬件定点处理数据与软件浮点仿真数据同时回馈到Matlab中比对，进行误差分析。

1基于逆QR分解的SMI波束形成算法

IQRD-SMI(逆QR分解SMI)算法，是在QR分解算法上的进一步改进，它能够回避QRD-SMI算法中的前后向回代问题，而且该算法仍能使用简单的Systolic阵列结构搭建，使权抽取操作得以全速并行实现，在软件编程与硬件实现中的便捷性大大提升。

设采样数据矩阵X为n次快拍得到的M*n维阵，即

(1)

传统采用QR分解SMI算法首先通过对协方差矩阵Rxx的估计，避免了直接使用Rxx矩阵去求解线性方程。然后使用酉矩阵Q通过Givens旋转对采样矩阵QR分解，最终化简为通过求解如(2)式所示的线性方程组来取得自适应权值w：

(2)

式(2)中，s为导向矢量；An是上三角阵，通过使用n*n维酉阵将xn三角化而得到；对数据矩阵xnQR分解的常用方法有Givens旋转和CORDIC算法。通过前向回代和后向回代的方法，可分别对式(2)中的上三角阵与下三角阵求解，从而得到自适应权w[12].

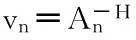
其算法实现步骤如下：

2)k=1,2,…,递推更新。

首先，计算中间向量z(n) = [An-1-H]*x(n)

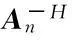
2脉动阵(Systolic阵)

Systolic英文解释为“心脏收缩”， H.T.Kung根据心脏按节拍收缩而使血液流至全身的原理提出了Systolic阵列结构，Systolic阵由一系列仅具有单一功能的处理单元(PE)构成，每个PE结构简单、易于实现、耗时耗能少，所有的PE单元都在有节拍的同步运行，系统工作时将从存储器中按节奏抽取数据并压入脉动阵，沿途经过并行的PE流水线，由于脉动阵列的结构特点，使数据能够高效、连续地完成整个处理过程。脉动阵结构原理如图1所示。

图1　Systolic脉动阵列结构原理框图

以4阵元为例，应用Givens旋转IQRD-SMI算法的三角脉动阵列 (GR-TSA,Givens Rotation-Triangular systolic array)示意图详见图2。

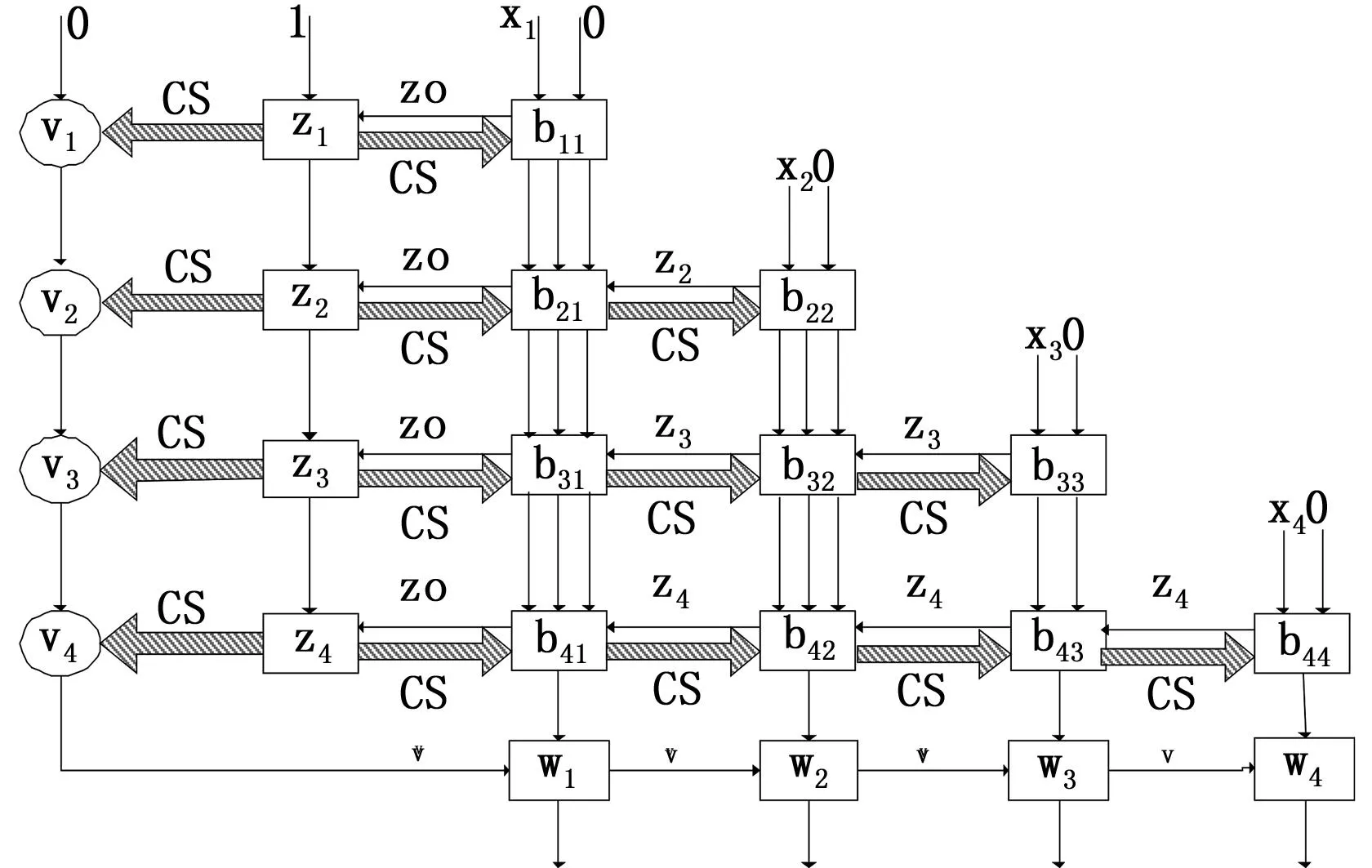
图2　IQRD-SMI算法GR-TSA阵示意图

内部各单元具体功能阐述如下：

1)bPE单元

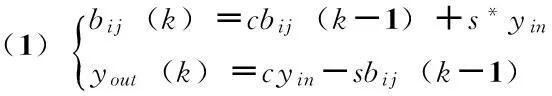
(4)xout=xin

2)zPE单元

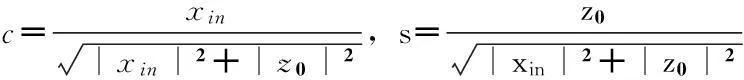
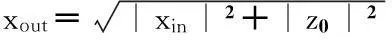
3)vPE单元

yout=vi

4)wPE单元

(1)当非对角元bij到来时完成乘积累加；wi(k)=zoutyin+wi(k-1);

(2)当对角元bii到来时完成乘积累加后输出wi并清零；

3IQRD-SMI算法的FPGA优化及实现

3.1CORDIC技术

GIVENS旋转运算需要进行开方与除法操作，这些运算会消耗大量的硬件资源，造成系统功耗过高的问题，从而达不到设计标准。此时引入CORDIC(coordinate rotation digital computer)技术来实现Givens旋转。CORDIC技术的基本思想是将一组固定的角度θi利用循环迭代算法，通过不断地摆动进而逼近所需旋转的角度θ。由于仅需移位和加/减法即可完成CORDIC运算，这样大大节约了FPGA硬件资源，非常适合在FPGA系统上实现。

基于CORDIC的无开方复数GIVENS旋转思想[13]，采用多个CORDIC单元依次完成复数转化实数的相位翻译、实数值与前一时刻值的相位翻译，从而得到GIVENS变换的相位，再经过直接数字式频率合成器DDS(Direct Digital Synthesizer)就能得到角度值，进而经过systolic阵的依次处理实现矩阵的QR分解。

3.2IQRD-SMI算法脉动阵结构的FPGA实现

脉动阵列FPGA实现的核心模块是旋转单元(bPE)，旋转单元实现步骤：

1)进行两次CORDIC旋转：首先使用CORDIC核来实现对输入数据求模，取得输入数据的模|xin|和旋转角θ。再次使用CORDIC核来求得x′和旋转角φ；

2)计算旋转角θ和φ的正余弦值，并计算c,s。

旋转单元FPGA模块化如图3所示。

图3旋转单元的FPGA模块化框图

IQRD-SMI脉动阵列结构的完整FPGA实现同图3所示，在顶层模块中通过时序、寄存器和控制口来操控数据的采集处理节拍与流向。

3.3改良的复用FPGA实现结构 (GR-ITSA,Givens rotation-Improved triangular systolic array)

FPGA芯片内部集成了常用的硬件资源，如DSP Slices、乘法器等，但是这些资源的数量有限。传统systolic阵列结构会随着阵元数的增加而大大消耗硬件资源。为了节约成本、降低硬件资源消耗，在传统IQRD-SMI算法的systolic阵列上进行改进，得到了低消耗的复用脉动阵结构GR-ITSA，如图4所示。

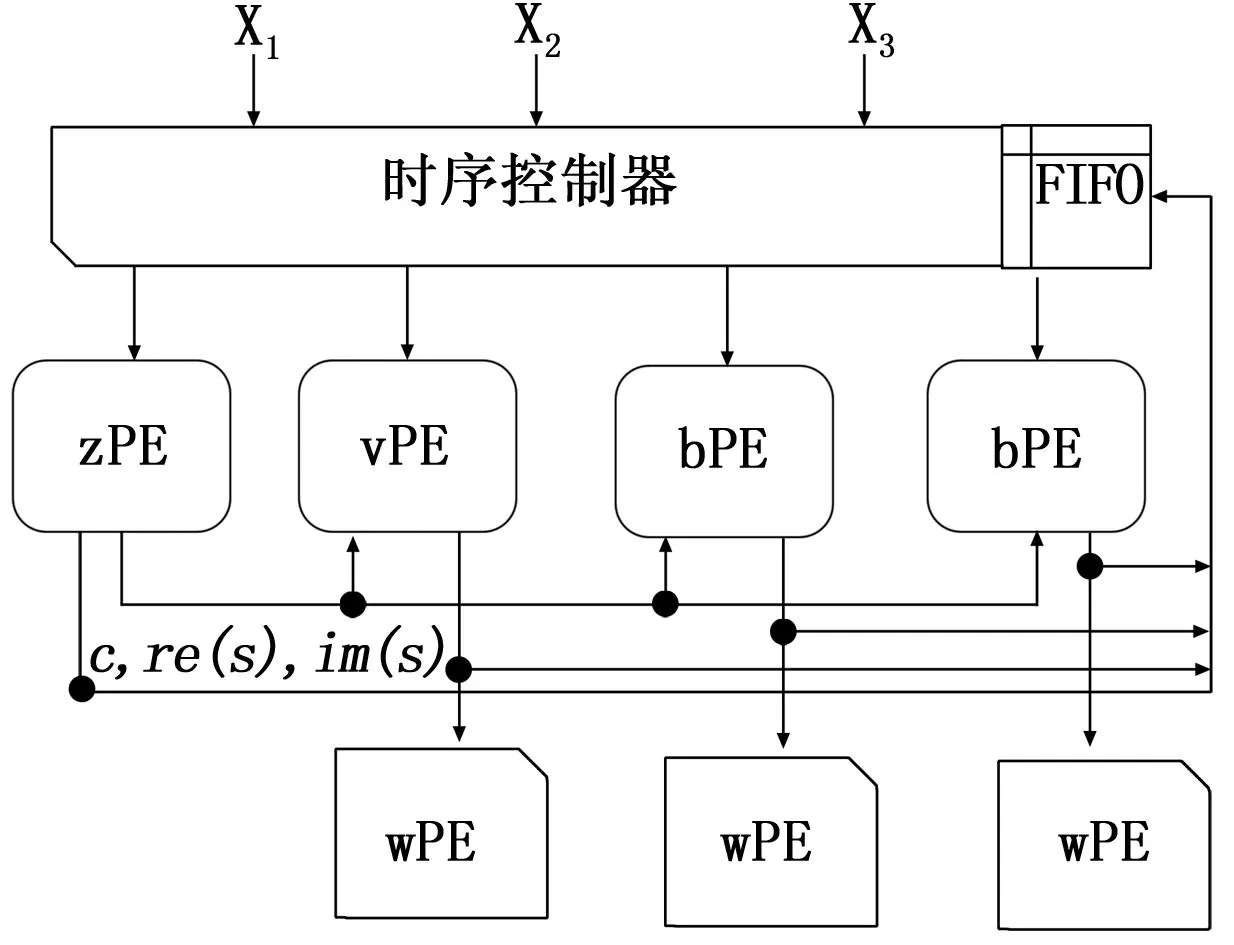
图4　GR-ITSA复用脉动阵列结构

关键的修改是在原阵列结构的基础上增加了时序控制器和用于存储中间量的FIFO。各PE单元实现的基本功能与传统结构一致，时序控制单元主要调度各PE的数据采集处理节拍，并含有寄存器(Block RAM)，用来接收和传递相应数据到各PE端口。

时序控制单元包含5种先入先出数据寄存器(FIFO):FIFO_Data、FIFO_bPE、FIFO_CS、FIFO_vPE、FIFO_wPE。FIFO_Data由M对宽度为L(M为阵元个数，L为量化后的接收数据位宽)、深度为N(N为采样快拍总数)的FIFO构成，用来缓存接收到的采样数据，并将数据提供给bPE。FIFO_bPE、FIFO_vPE、FIFO_wPE由深度为N的FIFO构成，用来接收各个PE单元的输出数据并为下一次的计算提供数据。FIFO_CS由3个FIFO构成，用来缓存bPE单元计算输出的C、S，并将C、S送至bPE和vPE单元。

5种FIFO与4类PE单元完成一次数据阵的QR分解需多个步骤，期间4类PE单元和5种堆栈在不同的时间段被调用，实现硬件资源共享。

4IQRD-SMI 算法的软硬件仿真及误差分析

4.1仿真结果

首先使用Matlab模拟生成信号源，通过Verilog I/O接口文件将信号数据输入到ISE程序中，并在Modesim软件下进行FPGA定点仿真验证，最后将输出结果返回Matlab，同Matlab中的浮点仿真计算结果进行比对。仿真参数如表1所示，仿真结果如图5所示。

表1　仿真参数设计

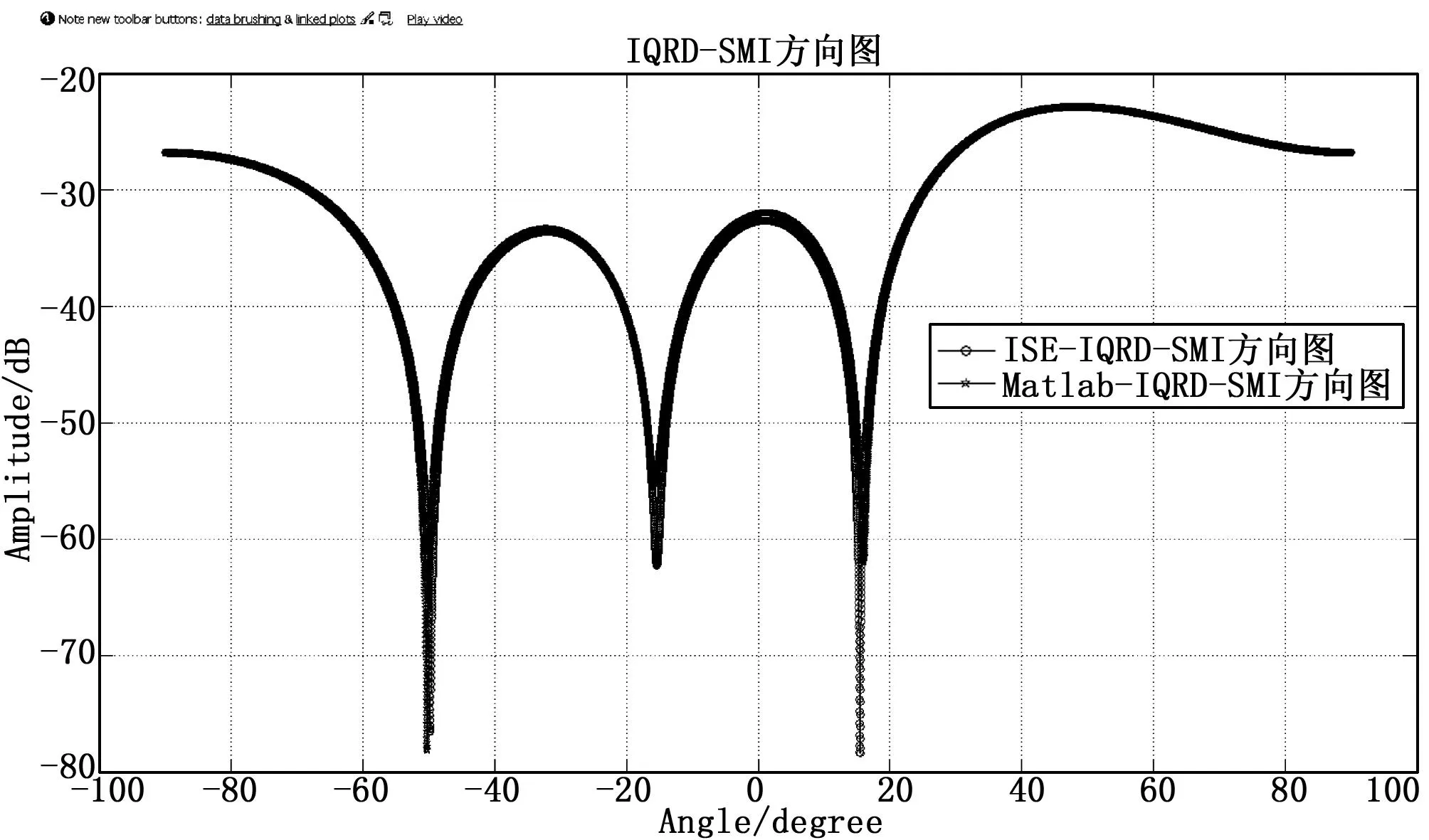
图5　ISE与Matlab仿真结果对比图

IQRD-SMI算法在Matlab软件浮点仿真与FPGA硬件定点仿真的对比波束如图6所示，仿真采用的采样数为64次快拍，满足基本采样数大于2 M的条件。通过对比图可知，改进的GR-ITSA结构实现了逆QR分解自适应波束形成算法，权向量得以高效实时的获取，在波束的期望方向theta= 50°处，算法对信号的增益值达到最大。

4.2误差分析与资源消耗

为了得到该算法的平均误差百分比，将复用结构FPGA定点计算与MATLAB浮点计算的结果引入误差计算公式(3)，取算术平均值作为最后的结果。

(3)

其中:rise表示FPGA硬件处理的结果，rmat表示Matlab浮点计算的输出，最终计算得到的误差百分比为0.38%。由误差数据看出，复用的FPGA结构在自适应权向量的抽取上具有高度的一致有效性。

当采样数据宽度为32bit，FPGA芯片采用xc7k325t时，观察表2中不同设计结构的硬件资源消耗。

由表2可知，当阵元数较小时，传统GR-TSA结构和改良的GR-ITSA结构都可以考虑作为自适应波束形成算法的实现结构，但是当sensor数大于等于4时，传统GR-TSA结构硬件资源消耗极大，不再具有实用性，观察此时的XtremeDSPSlices消耗发现，复用的GR-ITSA结构能减少的消耗达38%以上。

表2　不同硬件结构下的资源消耗

5结论

为了避免自适应算法中复杂的权抽取，首先研究了改进的逆QR分解SMI自适应算法，接着运用Systolic阵列，将算法的FPGA实现结构GR-TSA搭建出来。又研究了FPGA实现中各PE的具体实现方法，其中用到了CORDIC技术与DDS技术。最后在传统Systolic阵列结构的基础上改进，给出了复用的GR-ITSA阵列结构，并做了硬件定点仿真与软件浮点仿真的回馈分析。通过定量分析，复用结构可以显著降低资源消耗，在实际工程应用有效节约了成本。

参考文献：

[1] 宋丹, 曲绍君, 李高鹏. 基于失配处理的自适应干扰抑制系统[J]. 计算机测量与控制, 2012, 20(2): 480-483,499.

[2] 包志强, 丁康利, 单洁. 基于脉动阵的自适应波束形成算法仿真[J].无线通信技术, 2014,23(2):1-5,10.

[3] 宋博, 岳翠苹, 孙晶冬,等. 自适应数字波束形成的研究与实现[J].电视技术,2014，38(3).

[4] 戴凌燕. 自适应波束形成技术应用基础研究[D].长沙：国防科学技术大学研究生院,2009:2-16.

[5] 黄飞. 阵列天线快速自适应波束形成技术研究[D].南京：南京理工大学,2010:16-20.

[6] 刘倩. 阵列天线自适应波束形成算法研究[D].大连：大连理工大学,2008:7-10.

[7]TeitelbaumK.AFlexibleprocessorforadigitaladaptivearrayradar[J].IEEETrans.SystemsMagazine,1991,AES(5):18-22.

[8] 龚耀寰. 自适应滤波时域自适应滤波和智能天线[M].北京:电子工业出版社, 2003.

[9] 王永良. 空时自适应信号处理[M].北京:清华大学出版社,2000.

[10] 冯地耘, 陈立万, 王悦善. 自适应波束形成与高性能DSP[M].2007年9月第一版.成都：西南交通大学出版社，2007.

[11] 刘千里. 基于FPGA的逆QR分解SMI算法的并行实现方法[J].计算机工程与应用,2012,48(26):71-75,161.

[12]RaderCM.VLSISystolicarraysforadaptivenulling[J] .IEEESignalProcessingMagazine, 1996,13(7):29-49.

[13] 龚耀寰, 李航, 苟仲文. 基于CORDIC的无开方GIVENS旋转处理方法[J].电子科技大学学报(自然科学版),1997,26(6):565-569.

Research and FPGA Optimization Implementation of IQRD-SMI Algorithm Based on Systolic Array

Liu Yutao, Bao Zhiqiang, Li Longlong, Su Zihao

(Xi’an University of Posts and Telecommunications, Xi’an710061,China)

Abstract:For the problem of the weight values need a large amount of calculations in the adaptive beam-forming system, studied the inverse QR decomposition algorithm based on LCMV (IQRD-SMI algorithm) and the structure of traditional Systolic array GR-TSA, built with systolic array structures and simulated in Matlab. The principle of CORDIC technology is analyzed and how to use it on FPGA implement systolic array processing unit. On the basis of this, Based on the reuse of systolic arrays IQRD-SMI algorithm structure is given, Compared it with existing in the literature. Underlying design based on IQRD-SMI algorithm and hardware simulation based on systolic array be realized with xc7k325t in Xilinx FPGA, And the FPGA fixed-point simulation data and the computer floating-point simulation data contrast. The system and error is analysed.

Keywords:adaptive beamforming algorithms; FPGA; Matlab; systolic array; CORDIC techniques; GR-ITSA

文章编号：1671-4598(2016)02-0239-03

DOI：10.16526/j.cnki.11-4762/tp.2016.02.066

中图分类号：TN975

文献标识码：A

作者简介：刘禹韬(1988-)，男，辽宁锦州人，硕士研究生，主要从事信息处理技术及应用方向的研究。

基金项目：国家自然科学基金资助项目(61271276)；陕西省自然科学基金资助项目(2012JQ8011)。

收稿日期：2015-08-21；修回日期：2015-09-17。