四旋翼飞行器航姿参考系统的误差补偿方法研究

杨志永，毕德学，孟　强，王济阳

(1.天津科技大学 机械工程学院，天津　300222; 2.独山子石化公司 乙烯厂橡胶联合车间，新疆 克拉玛依　833600)



四旋翼飞行器航姿参考系统的误差补偿方法研究

杨志永1，毕德学1，孟强2，王济阳1

(1.天津科技大学 机械工程学院，天津300222; 2.独山子石化公司 乙烯厂橡胶联合车间，新疆 克拉玛依833600)

摘要：航姿参考系统是四旋翼飞行器姿态控制和惯性测量的关键，基于MEMS的惯性导航系统长期稳定性较差，陀螺仪传感器和加速度计存在明显的零漂现象，因此在使用前必须对陀螺仪传感器和加速度计的误差系数进行标定；论文首先以航姿参考系统的陀螺仪和加速度计实时数据的采集与处理，并通过对陀螺仪和加速度计的误差产生原理的分析，提出了陀螺仪和加速度计的新型误差补偿模型，并推导了基于高斯牛顿法的误差补偿与标定方法，由此简化了标定过程，得到了标定结果； 实验结果表明了在不提高成本和降低精度的情况下该基于高斯牛顿法的误差补偿与标定方法的有效性。

关键词：航姿参考系统；高斯牛顿法；误差补偿与标定

0引言

航姿参考系统是四旋翼飞行器姿态控制和惯性测量的关键，它主要由加速度计、陀螺仪和磁力计构成，各传感器的数据通过控制器的解算之后得到飞行器的姿态角、加速度等信息，为飞行器的控制逻辑提供重要信息。随着现代科技的不断发展，特别是微机电技术(MEMS)的不断进步，许多高精度微机电系统得以广泛应用。由于基于MEMS的惯性导航系统具有体积小、重量轻、成本低、不受外界干扰等优点[1]，近年来在军事及民用领域正得到越来越广泛的关注[2]。

1MPU-6000传感器概述

本文四旋翼飞行器航姿参考系统实验平台采用了占用空间较小的InvenSense公司的MPU-6000，如图1所示。MPU-6000是全球首例整合性6轴运动处理组件，它整合三轴陀螺仪与三轴加速器于同一硅芯片上，内建的数字运动感测处理器(digital motion processor,DMP)可处理复杂的九轴运动感测融合算法。通过I2C接口可以连接额外的数字传感器进行拓展，如磁力计等，扩展之后就可以通过其I2C或SPI接口输出9轴信号，向应用端输出完整的9轴融合演算技术[3]。

图1　MPU-6000模块

2陀螺仪零点漂移补偿

陀螺仪具有良好的动态响应性能，但其静态响应性能不足，根据误差产生机制不同，MPU6000传感器陀螺仪误差主要有：零点漂移误差、标度因数误差、安装误差及随机噪声等[4]。当应用陀螺仪传感器时必须首先对误差进行标定，以提高测量的精度。

对MPU6000三轴陀螺仪传感器输出影响最大的是零点漂移和标度因数误差，此外，由于制造工艺的限制，陀螺仪3个敏感轴还不能做到完全正交，这样就会产生非正交误差，同时陀螺仪传感器在安装焊接过程中也会引入安装误差，它和轴间非正交误差作用效果相似，可按安装误差一并处理。

综合考虑三轴陀螺仪各种误差，依据误差补偿原理[5]可以得到如下公式：

(1)

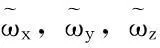
以上就是对陀螺仪的完全标定，由于ATMEGA芯片有限的内存和计算能力，并且测试时陀螺仪标度因数和交叉耦合项影响较小，这里只标记陀螺仪的零值偏移。由于忽略了标度因数和交叉耦合项的影响，可以大大简化标定方法。

为评估零点漂移的大小，使陀螺仪保持静止状态，此时陀螺仪的输出均应为零，但是受温度变化、电源电压不稳等因素的影响，静态工作点发生了变化，产生了零点漂移，输出结果和期望值并不一致，此时的误差记为零点漂移误差，MPU6000传感器陀螺仪漂移一般不超过0.04 dps。

为更准确地评估陀螺仪的零点漂移，陀螺仪静止后进行200次采样，将200次采样的均值作为零点漂移误差，当然，零点漂移误差不能超过0.04 dps，为此可以重复以上工作，找到更好的评估值作为零点漂移误差。

陀螺仪的零点漂移评估流程如图2所示。

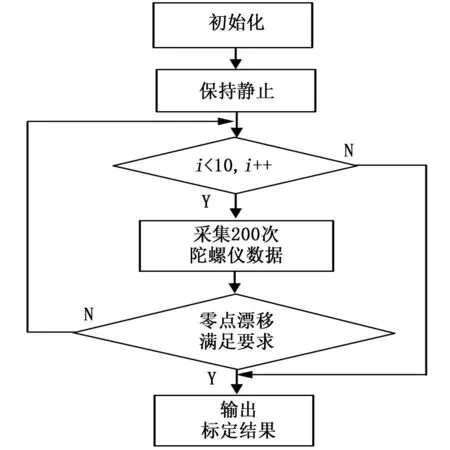
图2陀螺仪标定流程

3基于高斯牛顿法的加速度计误差补偿与标定

基于MEMS的惯性导航系统长期稳定性较差，存在明显的零漂现象，因此在使用前必须对传感器的误差系数进行标定。国内有很多加速度计方面的研究，加速度计标定的方法也比较多[6-7]。

3.1高斯牛顿法误差补偿与标定原理

一般的标定方法包括静态实验方法和动态实验方法两种。这两种方法或者精度较低，或者对转台等硬件精度需求较高，加大的成本投入，都存在一定的弊端[8]。为简化加速度计的标定过程，本文采用了新的高斯牛顿方法进行标定。

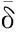
(2)

如果参数是正确的，且测量中没有噪声，那么无论加速度计传感器姿态如何，上式应满足：

(3)

即：

(4)

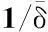
(5)

如果用xi，yi，zi表示第i次采样的读数值，那么第i次的采样误差可以写为：

(6)

现在可以正式描述本节所要解决的问题：

给定采样值(xi,yi,zi)(其中i=1,…,N)，找到合适的参数mx,my,mz,δx,δy,δz，以使罚函数：

(7)

尽可能地小。

这是典型的非线性最小二乘问题，为便于求解，通常把非线性最小二乘问题转化为一系列线性最小二乘问题求解，设x(k)是解的第k次近似，在x(k)将函数εi(x)线性化，这样就把非线性最小二乘问题转化为了线性最小二乘问题[9]。

在式(7)中，假设

(8)

其中：pi是n维列向量，bi为实数，x=(mx,my,mz,δx/G,δy/G,δz/G)T。令

(9)

A为m×n矩阵，b是m维列向量，则式(7)可以写成矩阵乘积形式：

(10)

E(x)的平稳点满足：

(11)

即：

(12)

对于线性问题，A列满秩，ATA为n阶对称正定矩阵，目标函数E(x)的平稳点：

(13)

而此处为非线性最小二乘问题，不能直接按上式计算。

将函数εi在点x(k)处进行一阶泰勒展开得：

(14)

令

(15)

用φ(x)近似E(x)，用φ(x)的极小点作为函数E(x)的极小点估计，求解线性最小二乘：

(16)

记Ak，ε(k)，b分别为：

则式(15)写成：

(17)

将Ak，b带入式(12)，得：

(18)

整理得：

(19)

(20)

其中:x(k+1)为罚函数E(x)极小点的第k+1次近似。式(18)就是高斯牛顿公式。d(k)为点x(k)处的高斯牛顿方向。为保证迭代之后函数值下降，求得方向d(k)后，从点x(k)起沿这个方向进行一维搜索：

(21)

求出步长λk后，令x(k+1)=x(k)+λkd(k)作为第k+1次近似。通过不断迭代，直到满足迭代次数或两次迭代差值满足要求，求得x值。

3.2高斯牛顿法标定加速度计步骤

1)给定初值x(1)=(0,0,0,1/G,1/G,1/G)T，允许误差σ>0，置k=1。

2)计算函数值εi(x(k))，i=1,2,…,6得到向量

(22)

再计算一阶偏导数

(23)

得到6×6阶矩阵：

(24)

3)解方程组

(25)

求得牛顿高斯方向d(k)。

4)从点x(k)起，沿d(k)进行一维搜索。求得步长λk，使得

(26)

令x(k+1)=x(k)+λkd(k)。

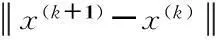
3.3加速度计标定及实验结果

为标定模型参数(公式5)，只需要找到6个待定参数：3个mi和3个δi。

对于1个观察点(x, y, z)得到一个含6个未知数的方程，6个相互独立的观察点得到含6个未知数的6个方程，并能确定唯一解。但是由于噪声的存在，这种方法也不准确。但是可以选择参数值，使误差尽可能地小。为确定这6个数，至少需要6次测量，假定采用6点标定法，依次测量平放、左90°放置、右90°放置、前倾90°放置、后仰90°放置和倒置6种位置(如图3所示)的数据。实验步骤如下：

1)将加速度计按图3中第一张图片Z上位置静止放好，测量获得此时零点的20组漂移数据。

2)按照1)，顺序按图3 中的加速度计的位置方式依次放好，测量获得每种姿态此时零点的20组漂移数据。直到六种姿态全部采集。在每个位置加速度计保持静止足够长的时间来收集样本，尽可能多地读取新数据，通过采样值求平均的(实验选20个点)方法减弱传感器在读数据时的噪声影响。

3)重复1)和210次以上，获得足够的零漂数据。其中一组数据如表1 所示。

4)实验根据数据，利用高斯牛顿法，标定出6个参数的值，如表1 所示。

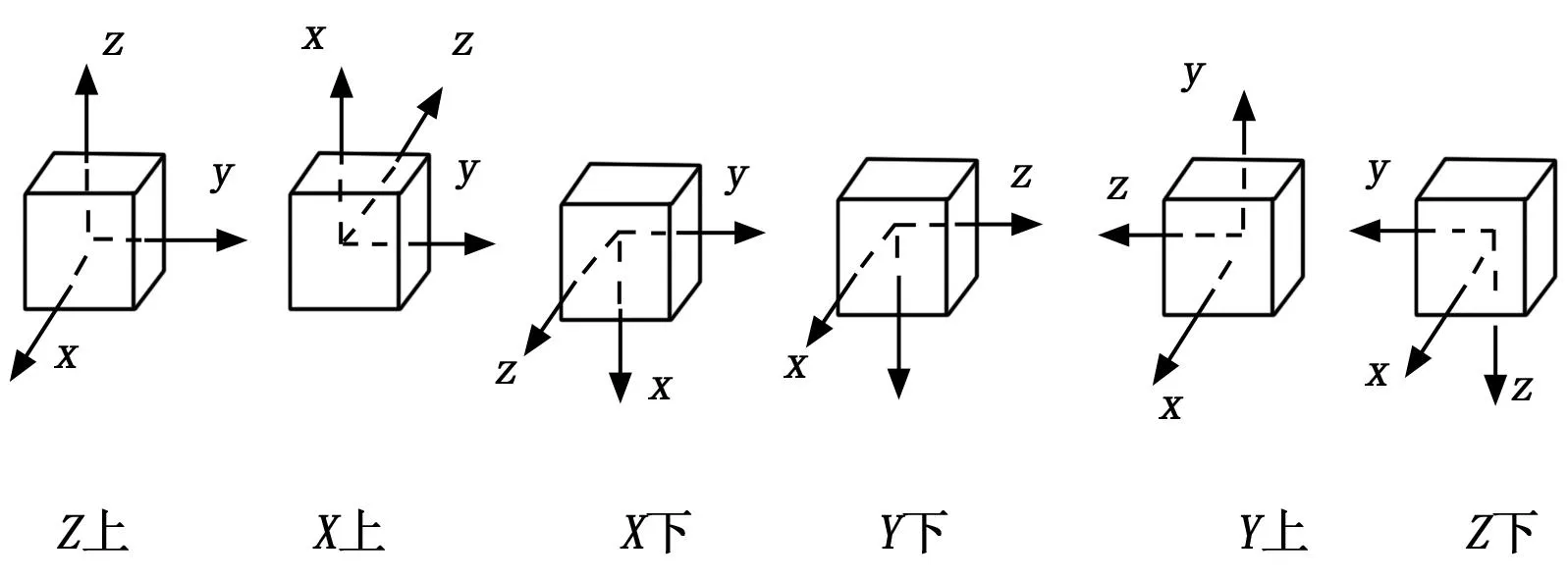
图3　加速度计的6种不同位置

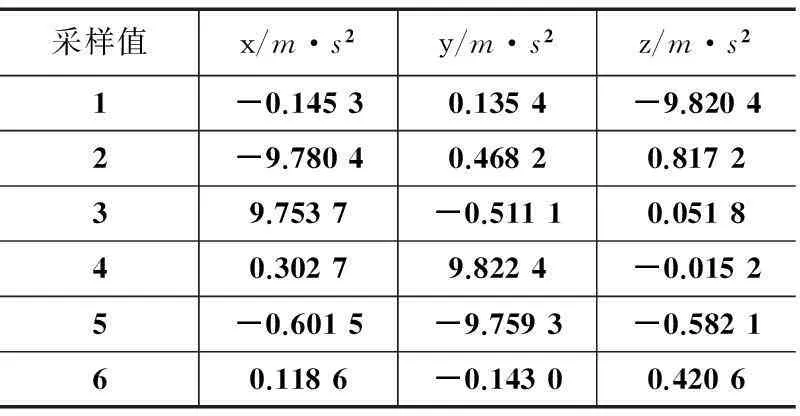
采样值x/m·s2y/m·s2z/m·s21-0.14530.1354-9.82042-9.78040.46820.817239.7537-0.51110.051840.30279.8224-0.01525-0.6015-9.7593-0.582160.1186-0.14300.4206

运用高斯牛顿标定方法，并采用Matlab程序进行标定，标定结果如表2所示。

4结论

本文主要以航姿参考系统的陀螺仪和加速度计数据采集与应用为基础，分析了陀螺仪和加速度计的误差产生原理，针对加速度计的标定提出了新型的高斯牛顿法标定法，简化了标定过程，得到了标定结果。

参考文献：

[1] 陈剑，孙金海,等．惯性系统中加速度计标定方法研究[J]．微电子学与计算机，2012，29(8)：130．

[2] 陆辰，李荣冰，刘建业,等．微型航姿系统中三轴MEMS加速度计组合误差建模方法[J]．测试技术学报，2011，25(1)：29．

[3]DataSheet.MPU-6000andMPU-6050RegisterMapandDescription[EB/OL].http：//www.Invensense．com，2011，11．

[4] 彭孝东，陈瑜,等．MEMS三轴数字陀螺仪标定方法研究[J]．传感器与微系统，2013，32(6)：63-64．

[5] 宋丽君，秦永元．MEMS陀螺仪的一种实用标定法[J]．压力与声光，2010，32(3)：372-373．

[6]SyedZF,AggarwalP,GoodallC,etal．Anewmulti-positioncalibrationmethodforMEMSinertialnavigationsystems[J]．MeasurementScienceandTechnology，2007，18(7)：1987-1907．

[7] 张红宇，叶新生．一种改进的IMU加表标定模型及快速标定方法[J]．理论与实践，2009(3)：11-13．

[8] 刘百奇，房建成．一种改进的IMU无定向动静混合高精度标定方法[J]．仪器仪表学报，2008(6):1250-1254．

[9] 张广军．机器视觉[M]．北京：科学出版社，2005．

Error Compensation and Calibration for Attitude Heading Reference System with Four-rotor Aircraft

Yang Zhiyong1，Bi Dexue1，Meng Qiang2，Wang Jiyang1

(1.School of Mechanical Engineering,Tianjin University of Science and Technology,Tianjin300222,China；2.Dushanzi Petrochemical Company, Ethylene&rubber Workshop,Kelamayi833600,China)

Abstract：Attitude heading reference system(AHRS)is the key part for four-rotor aircraft to its posecontrol and inertial measurement. The long-term stability of initial navigation system based on MEMS is poor, there exists obvious zero drift phenomenon, so error compensation and calibration of Gyro and Accelerometer must be completed before using it. Based on real time data collection and processing, and error producing analysis, this paper proposes a novel error compensation model for Gyro and Accelerometer, and this new error compensation and parameter calibration method based on Gauss-Newton algorithm is proposed. The method simplifies calibration procedure and obtains calibrated parameter value. Experimental results verify the effectiveness of the proposed method on the condition of no additional cost and accuracy loss.

Keywords：AHRS；Gauss-Newton algorithm；error compensation and calibration

文章编号：1671-4598(2016)02-0267-04

DOI：10.16526/j.cnki.11-4762/tp.2016.02.074

中图分类号：TH824

文献标识码：A

作者简介：杨志永(1987-)，男，河北唐山人，硕士研究生，主要从事嵌入式系统方向的研究。毕德学(1969-)，男，山东济南人，教授，硕士研究生导师，主要从事机器人方向的研究。

收稿日期：2015-09-01；修回日期：2015-10-15。