含有误差校正的小波神经网络交通流量预测

王秋平，舒　勤，黄宏光

(四川大学 电气信息学院，成都　610065)



含有误差校正的小波神经网络交通流量预测

王秋平，舒勤，黄宏光

(四川大学 电气信息学院，成都610065)

摘要：交通流量的准确预测对于高速路管理者进行决策至关重要;建立了小波神经网络(WNN)交通流量预测模型，并通过预测训练误差和测试误差校正预测结果来提高预测精度;首先构建WNN模型对交通流量进行初步预测，然后利用经验模态分解(EMD)和WNN模型对训练误差和测试误差进行预测;分别用训练误差预测值、测试误差预测值和两种误差预测值的加权对流量初步预测结果进行修正得到最终预测值;采用四川省成灌高速路交通流量数据进行了仿真对比实验，仿真结果表明含有误差校正的小波神经网络模型能有效提高交通流量预测精度，并且利用两种误差加权修正模型的预测精度高于利用测试误差的修正模型和利用训练误差的修正模型。

关键词：高速路交通流量；流量预测；小波神经网络；误差预测；经验模态分解

0引言

高速路交通流量是智能交通系统(intelligent transportation system, ITS)的重要组成部分。交通管理部门需要根据准确的交通流量预测对交通进行控制，以避免交通拥堵、车祸等情况；同样，出行者也需要通过准确的车流量预报决定其出行的时间、路线等[1-3]。因此，交通流量预测已成为交通领域研究的焦点之一。

影响高速路交通流量的因素有很多。交通系统是一个由车辆、道路和人参与的复杂系统，交通流量受当地经济、人们习惯、天气情况等各种非线性因素的影响。在节假日或者上下班时刻会存在流量高峰期；在一些特殊气候条件下，事故几率增加；另外，交管部门对高速路的检修也会影响高速路上车流量情况。以上这些因素使得高速路交通流量预测成为一个难题。

目前常用的交通流量预测方法有时间序列分析、Kalman滤波、人工神经网络、非参数回归[4-10]等。对于不同的数据、不同的模型存在各自的缺点，其预测的精度也不同。时间序列模型的理论相对比较成熟，但很难实现参数的动态调整；Kalman滤波模型是在线性最小方差估计的基础上提出的，它具有计算量小、实时性高等优点，但是无法描述交通流量非线性部分；非参数回归模型的回归函数灵活，拟合精度高，但结果外延性差；人工神经网络能够很好地描述数据的非线性性，却不适用于非平稳信号。小波神经网络(wavelet neural network，WNN)结合了小波分析和人工神经网络的优点，能够优先处理非平稳、非线性信号，很适合预测高速路交通流量，但其预测精度还不能满足实际的工程需要。

为此，笔者提出含有误差校正的小波神经网络交通流量预测模型。采用EMD-WNN方法分别对WNN的训练数据和测试数据的误差序列进行预测，利用误差预测值对WNN初步预测结果进行修正。该方法能够有效解决拐点处预测误差低的问题，并同时提高了预测精度。

1WNN交通流量预测模型

高速路交通系统是一个非线性的动态复杂系统，难以用数学方法准确建模。神经网络方法把未知系统看成一个黑箱，包含输入层、隐层和输出层。首先用已知的输入输出训练该系统，然后用已训练的网络进行预测。采用神经网络预测可以分为3步：1)神经网络构建；2)神经网络训练与测试；3)神经网络预测[11-13]。

WNN是一种以BP神经网络拓扑结构为基础，把小波基函数作为传递函数的神经网络。WNN结合了人工神经网络和小波分析的优点，具有网络收敛速度快，避免陷入局部最优，又有时频局部分析的特点，其拓扑结构如图1所示。

图1　WNN拓扑结构图

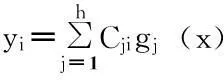
(1)

式中，gj(x)为隐层第j个节点的输出值；wij为输入层到隐层的连接权值；gj为小波基函数；bj为gj的平移因子；aj为gj的伸缩因子。文中采用的小波基函数为Morlet母小波基函数，其数学表达式为：

(2)

2含误差预测校正的预测模型

将已采集到的高速路交通流量数据分为训练数据x1、测试数据x2和预测数据x3。利用训练数据能够构建一个反映交通流量特征的合理预测模型，同时可得到预测模型对训练数据的误差e1。利用训练数据建立好模型之后，为了验证模型的合理性和可靠性，需采用测试数据对模型进行验证，验证过后可得到预测值和真实值之间的测试误差e2。误差序列e1、e2是和原始流量数据具有相同采样时间间隔的时间序列，同样可以建立它们的预测模型，文中称之为误差预测模型。

虽然小波神经网络克服了BP神经网络的缺点，能够有效处理非线性数据。但是相对于原始交通流量序列，误差序列规律性弱，随机性强，是一种多频率信号，用单一的WNN模型很难准确描述误差序列。如果误差预测不准确，当预测误差和预测值叠加后，预测值将偏离真实值更远。所以，准确预测误差是实现该算法的关键。为了提高误差的预测精度，引入EMD算法，根据误差序列的时间尺度特性将误差序列分解为若干个具有单一频率的本征模态函数(intrinsic mode function, IMF)[14]。再对每个IMF采用小波神经网络进行预测，最后将预测值叠加得到最终的误差预测结果。

文中提出3种方法来修正预测值p：1)对e1进行预测得到pe1，p’=pe1+p；2)对e2进行预测得到pe2，p’=pe2+p；3)考虑两种误差的预测修正模型，p’=w1pe1+w2pe2+p，式中w1、w2为权值，并且满足w1+w2=1。含误差预测校正的交通流量预测模型的流程如图2所示。

图2　含误差校正的预测流程图

3预测方法实例分析

3.1实验数据的选取

文中实验数据来源于四川省成灌高速路2013年7月8日~8月6日的实测交通流量数据，每隔5 min采样一个数据，可记为{di,i=1,2,…,n}。将前28d的数据作为训练数据集x1，第29天的数据作为测试数据x2,第30天的数据作为预测数据集x3。图3显示了一部分原始交通流量数据。从原始序列图中可以看出，高速路交通流量具有以日为周期的周期性，并且存在早晚高峰期，早晚高峰期的波动较大。

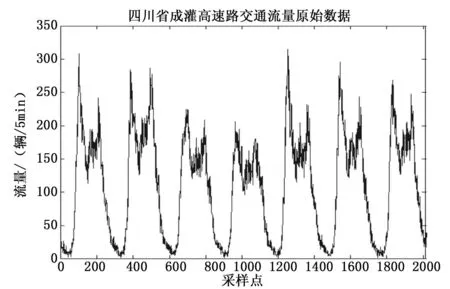
图3　成灌高速路7月交通流量数据

3.2小波神经网络初步预测

基于Matlab软件[15-17]，利用训练数据集x1建立小波神经网络预测模型，对预测数据集x3进行预测。实验结果如图4所示。从图中可以看出，WNN预测交通流量的整体误差较小，特别是从凌晨到早上9点和晚上8点到凌晨这两个波动性相对较小的时间段，预测比较准确，但是在交通流量拐点和高峰时期，预测误差较大。利用误差预测对模型进行修正后，拐点处和高峰时期的预测精度将明显改善。

图4　交通流量WNN初步预测结果

3.3预测误差校正结果

EMD-WNN预测误差的方法可以分为3个步骤：1)对误差序列进行EMD分解；2)用WNN对各个频率的分量进行建模预测；3)重构生成误差序列的最终预测值。

基于EMD-WNN方法，采用第2节所述的3种误差方法对误差进行预测。当进行加权误差预测时，经过多次实验，可得到权重系数w1=0.4，w2=0.6。将3种误差预测值和初步高速路流量预测值进相加得到流量最终预测值，如图5~7所示。

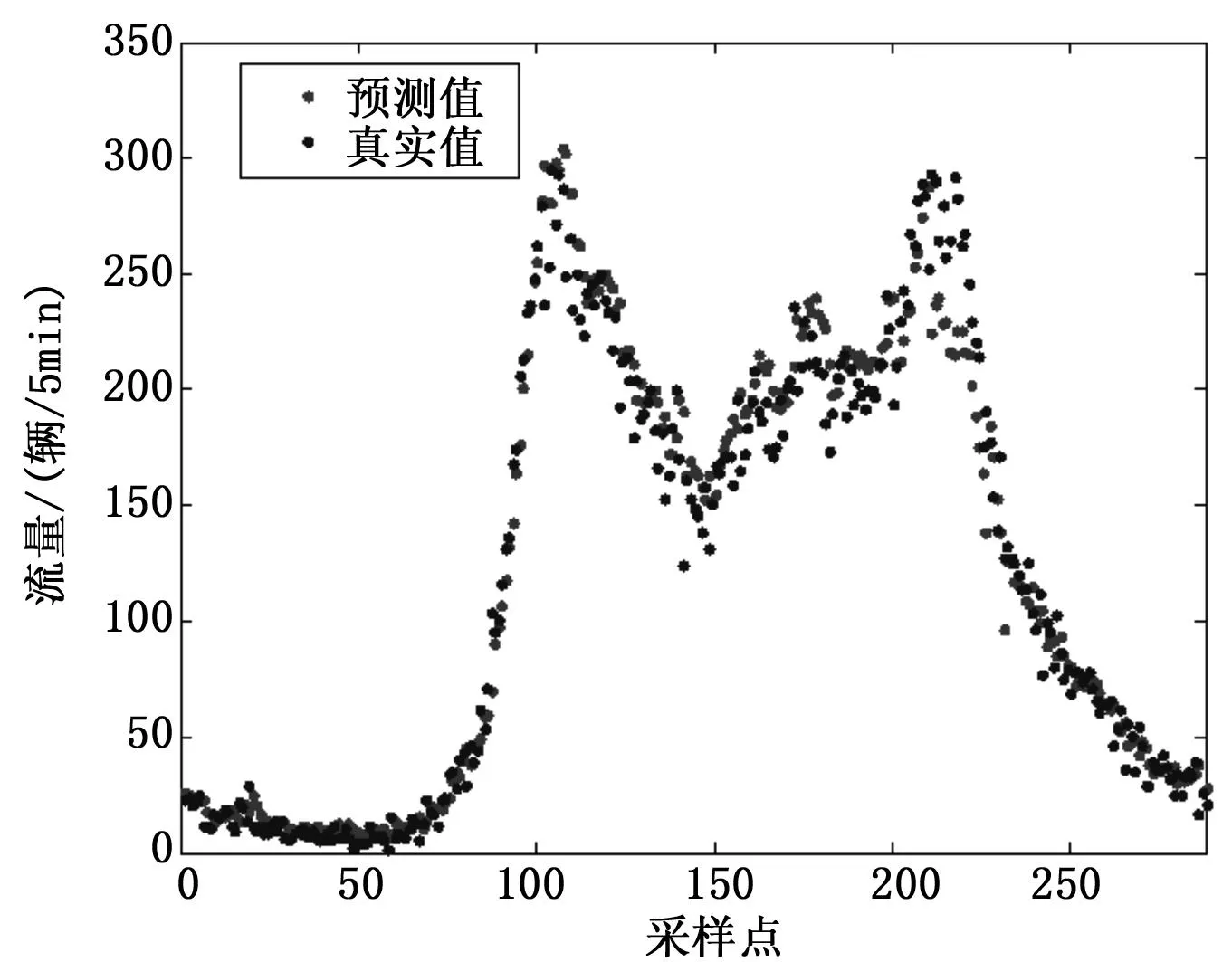
图5　预测训练误差校正WNN结果

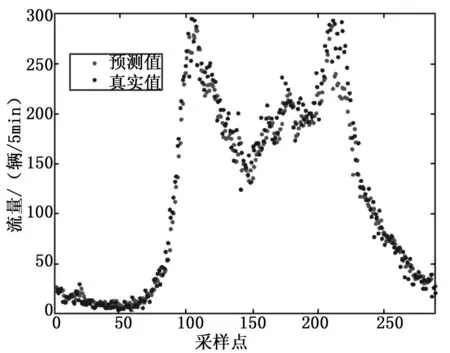
图6　预测测试误差校正WNN结果

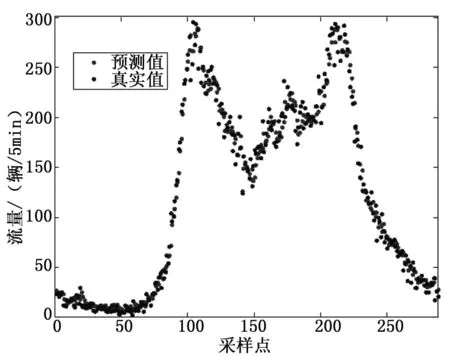
图7　两种误差加权校正WNN结果

从3幅结果图中均可看出，3种误差校正方法在一定程度上提高了拐点处和流量波峰处的预测精度。为了定量评价3种方法的预测效果，文中选用平均绝对百分误差(MAPE)和均方误差(MSE)度量预测模型的精度，其定义为：

(3)

其中:d(i)为真实流量数据，p(i)为预测模型输出的预测数据。3种方法的预测误差对比如表1所示。

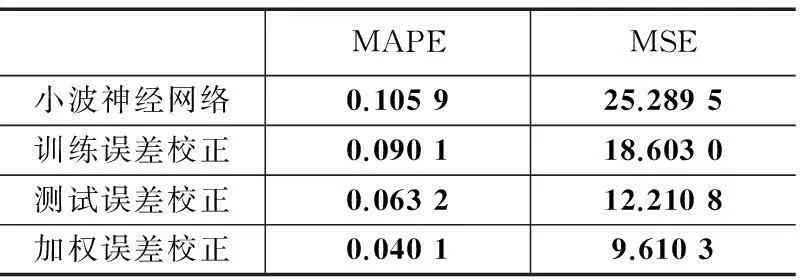
表1　预测模型指标对比

仿真结果表明，含有误差校正的模型的预测精度均有所提高。其中预测训练误差校正模型的MAPE为0.0901，预测测试误差校正模型的MAPE为0.063 2，加权误差校正模型的MAPE为0.040 1。训练误差是因为采用已知样本对预测模型进行训练时而产生的误差，这种误差是因为欠训练或者过训练而造成的；测试误差是因为模型对未知样本进行预测而产生的误差。相对于训练误差，测试误差更能体现待预测样本误差的规律和特征，所以采用测试误差校正预测结果比较有优势。但是当考虑两种误差时，更能全面反应待预测样本误差序列的特征，进一步提高预测精度。

4结论

由于高速路交通流量数据是非平稳非线性信号，现有的预测模型还不能满足实际的工程需求。本文在分析现有的交通流量预测模型的基础上，采用含误差校正的小波神经网络预测模型，提出了3种误差校正方法。第一种是利用训练数据的误差校正初步预测值；第二种是利用测试数据的误差校正初步预测值；第3种是考虑两种误差模型来校正初步预测值。仿真结果表明，文中所建模型能显著提高交通流量预测精度，且能解决拐点预测误差大的问题。

参考文献：

[1] 孙棣华, 李超, 廖孝勇. 高速公路短时交通流量预测的改进非参数回归短发[J]. 公路交通科技, 2013, 30(11).

[2] Chiou J M. Dynamical functional prediction and classification with application to traffic flow prediction[J]. The Annals of Applied Statistics, 2012, 6(4):1588-1614.

[3] 金玉婷, 余立建. 基于小波神经网络的短时交通流预测[J]. 交通科技与经济, 2014, 1(16): 82-86.

[4] 姚智胜. 基于主成分分析和支持向量机的道路网短时交通流量预测[J]. 吉林大学学报(工学版), 2008,38(1) : 48-52，112-118.

[5] 张涛, 陈先, 谢美萍,等. 基于K近邻非参数回归的短时交通流预测方法[J]. 系统工程理论与实践， 2010, 30(2): 376-384.

[6] 沈国江, 王啸虎, 孙祥杰,等. 短时交通流量智能组合预测模型及应用[J]. 系统工程理论与实践， 2011,31(3):562-570.

[7] 郑长江, 陈田星．基于小波神经网络的路段短时交通流预测[J]. 大连交通大学学报，2012, 33(5) : 50-53.

[8] 李波. 基于小波分析和遗传神经网络的短时城市交通流量预测[D]. 北京: 北京交通大学,2012.

[9] 王进, 史其信. 短时交通流预测模型综述[J]. 中国公共安全(学术版), 2005,(1):92-98.

[10] 戴文战, 娄海川, 杨爱萍. 非线性系统神经网络预测控制研究进展[J]. 控制理论与应用, 2009, 26(5): 521:230.

[11] 刘宁, 陈昱颋, 虞慧群,等. 基于 Elman 神经网络的交通流量预测方法[J]. 华东理工大学学报(自然科学版), 2011, 2(37):204-209.

[12] 候媛彬, 杜京义, 汪梅. 神经网络技术[M]. 西安:西安电子科技大学出版社,2007.

[13] 郭文, 乔宜正. 基于遗传优化神经网络的铁路客运量预测研究[J]. 山东理工大学学报(自然科学版), 2008,22(3):25-28.

[14] 潘亮. 基于EEMD-GSVM的高速铁路短期客流预测[D]. 北京: 北京交通大学,2012.

[15] 陈振伟, 郭拯危．小波神经网络预测模型的仿真实现[J]．计算机仿真, 2008,25(6) : 147-150．

[16] MATLAB中文论坛. MATLAB 神经网络30个案例分析[M]. 北京: 北京航空航天大学出版社, 2014．

[17] 葛哲学, 孙志强. 神经网络理论与MATLAB R2007实现[M] . 北京: 电子工业出版社, 2007.

Wavelet Neural Network with Predict Error Correction in Traffic Flow Prediction

Wang Qiuping, Shu Qin，Huang Hongguang

(School of Electrical Engineering and Information, Sichuan University, Chengdu610065,China)

Abstract:An accurate predict of traffic flow is critical for highway managers to make decisions. A wavelet neural network (WNN) model was established for forecasting traffic flow, at the same time, the prediction accuracy was improved by the training-error and test error correction. WNN model was established for a preliminary prediction of traffic flow, and then EMD-WNN model was proposed to forecast the train-error and test error. Finally, the correction of preliminary prediction values was carried out by predictive value of training-error, test-error and weighted value of the two kind of errors respectively. The contrastive experiments were carried out using the actual traffic flow data on Cheng-guan highway in Sichuan province. The results show that the prediction accuracy was improved by the WNN model with error correction, and prediction accuracy is highest when the weighted-error- correction is used.

Keywords:highway traffic flow; flow prediction; wavelet neural network; error prediction; empirical mode decomposition

文章编号：1671-4598(2016)02-0168-03

DOI：10.16526/j.cnki.11-4762/tp.2016.02.046

中图分类号：U491

文献标识码：A

作者简介：王秋平(1990-)，女，四川宜宾人，硕士研究生，主要从事数据处理和现代信号处理方向的研究。

基金项目:四川省交通科技项目(2013c7-1)。

收稿日期：2015-07-23；修回日期：2015-08-18。

舒勤(1958-)，男，四川成都人，博士，教授，主要从事现代信号处理，智能电网方向的研究。