基于混合S参数法的微带线耦合效应研究
2016-03-17韩帅涛侯德亭
韩帅涛,侯德亭
(1.解放军信息工程大学 理学院,郑州 450001; 2.63880部队,河南 洛阳 471000)
基于混合S参数法的微带线耦合效应研究
韩帅涛1,2,侯德亭1
(1.解放军信息工程大学 理学院,郑州450001; 2.63880部队,河南 洛阳471000)
摘要:采用混合S参数法研究了入射波和集总电源共同激励下微带线的终端响应,对于微带线上的传输线模式波和天线模式波的计算采用了Galerkin积分方法,避免了采用广义函数束方法(GPOF)从仿真结果中提取信号的过程,从而简化了计算步骤,减少了计算时间;通过与电磁仿真软件HFSS仿真结果的比较,验证了该方法的正确性;并采用混合S参数方法计算了不同微带线参数对耦合效应的影响,研究表明,当微带线长度变长,宽度变宽,介质基板厚度变厚,介质基板相对介电常数变大时,耦合效应变强,其中耦合效应受长度影响最大。
关键词:电磁耦合;传输线理论;混合S参数;PCB
0引言
电磁波对传输线网络的影响一直是电磁领域研究的重要问题,而随着电子技术的发展以及电子设备的广泛应用,电磁波对电子设备重要组成——PCB的耦合研究也变得越来越重要。对于该问题的研究主要有数值计算方法,解析算法以及实验研究方法。其中,数值计算方法[1]需要消耗大量的内存和时间,因此计算效率不高,不具有较强的通用性。解析算法最初是采用多导体传输线理论(MTLT)来分析电磁波对传输线网络的耦合的[2-4],其在低频段的分析有较好的精确性,但并不适用于高频的精确分析。Leone等人[5-6]基于BLT方程就电磁波对微带线的耦合进行了分析,研究了不同入射方式,脉冲波形对微带线终端的影响;Tesche等人[7]将频域BLT方程扩展到了时域BLT方程,并用时域BLE方程法计算了均匀有耗微带线的瞬态终端响应电压,但是该方法对于非线性终端负载的计算需要进行卷积计算,计算繁琐,因此通用性不强。Bayram等[8-10]利用电路分析软件和全波仿真软件相结合的方法来计算终端电压,取得了较好的计算精度,但是其对于微带线上天线模式波和传输线模式波的计算需要先进行仿真,然后采用广义函数束法提取其中的信号,计算过程较为繁琐。本文首先通过传输线模型结合Galerkin积分方法[11]计算了入射波在微带线上的传输线模式波和天线模式波;然后通过仿真软件得出微带线开路状态下的S参数矩阵,将由入射波产生的模式电压和开路状态下的S参数矩阵结合起来,通过公式转化提取出表示模式电压对PCB端口电压影响的混合S参数矩阵;最后,将混合S参数矩阵以及代表天线模式波的恒定电压源导入到射频电路仿真软件ADS,从而计算微带线端接不同负载时的端口电压。
1混合S参数模型的构建
1.1微带线电场分布
如图1所示,当电磁脉冲以入射角θ、方位角φ、极化角γ入射到印制电路板上时,电磁波会在介质板的分界面发生反射、透射等现象[12]。

图1 入射波照射微带线示意图
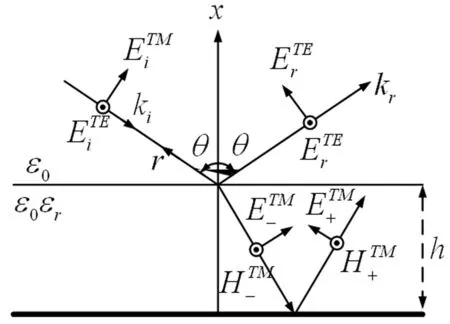
图2 入射波的矢量分解
对微带线上的电磁波进行波矢量分析,求解微带线上的电场强分布。入射平面波矢量分析如图2所示,其中kz=k0sinθcosφ,kir=krr=kzz,反射波与入射波的关系可由介质板上的反射系数RTE,RTM表示,式(1)计算微带线导体带上的横向电场:
(1)
(2)
(3)
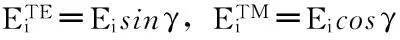
(4)
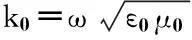
假设地板是良导体,横电波的反射系数RTE和横磁波的反射系数RTM分别由下式给出:
(5)
(6)
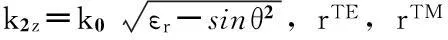
(7)
(8)
1.2微带线终端开路电压
由线天线Pocklington方程可知,当微带线宽度远小于入射波波长且微带线长宽比远大于1时,可以用微带线中心线上z方向的电流代替微带线表的面电流。对于无限长微带线来说,该电流和入射波有一样的z方向传播参数,即天线模式电流,可以用式(9)表示:
(9)
当微带线为有限长且终端负载又不匹配时,I0(z)将在微带线终端反射产生新的电流分量,这个电流分量称为传输线模式电流,传输线模式电流以c=3×108m/s在微带线上传播,传输线模式电流分为前向波和后向波,因此有限长微带线上的总电流可以表示如下:
(10)
式中,Cn是由微带线尺寸,介质等决定的常量,Bn(z)表示传输线上不同模式电流。
由Pocklington积分公式可知
(11)

(12)
根据Galerkin计算方法可以得到式(13)所示3×3矩阵
(13)
式中,
(14)
(15)
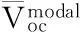
1.3混合S参数模型
2端口微带线网络可以用式(16)所示2阶S参数矩阵表示不同端口入射波与散射波之间的关系:
(16)
由上面的分析可知,天线模式波与微带线的端接负载无关,仅由入射波决定,而传输线模式波对各端口响应的影响则根据端接负载的变化而变化。为计算传输线模式波对微带线各端口终端响应的影响,本文将传输线模式波作为第3端口,并据此修正S参数矩阵。
(17)


(18)
其中:
(19)
由于天线模式波和端口负载无关,仅由入射波和微带线结构、材料决定,所以在电路分析中可以将其等效为恒定电压源;VEMI为表示传输线模式波的第3端口,从而可以得到如图3所示的3端口的混合S参数模型电路图。将所得电路图导入射频电路分析软件ADS,就可以求得该微带线网络在入射波照射下端接不同负载的端口电压。

图3 混合S参数等效电路图
2计算验证及实例分析
如图4所示为一微带线示意图,长l为40 mm,厚度h为0.787 4 mm,导体带宽度w为2 mm,介质基片材料的相对介电常数εr为2.2,终端接一10 mA集总电流源和100 Ω的终端负载。入射波入射角度θ为45°,方位角φ为45°,极化角γ为45°,电场强度Ei为2 000 V/m。

图4 微带线示意图

图5 电压幅度对比图

图6 电压相位对比图
本文研究了集总电流源从1 mA到10 mA情况下终端负载上的感应电压值,并将该结果与电磁仿真软件HFSS的仿真结果进行了对比,结果表明混合S参数矩阵方法与全波仿真结果基本一致,证明了混合S参数方法的正确性,但是采用电磁仿真结果所需时间为30 min,采用广义函数束提取信号方法所需时间为3 min,而采用混合S参数方法所需时间仅为1 min,由此可见混合S参数方法大大减少了计算时间,提高了计算效率。

图7 不同微带线长度的终端电压
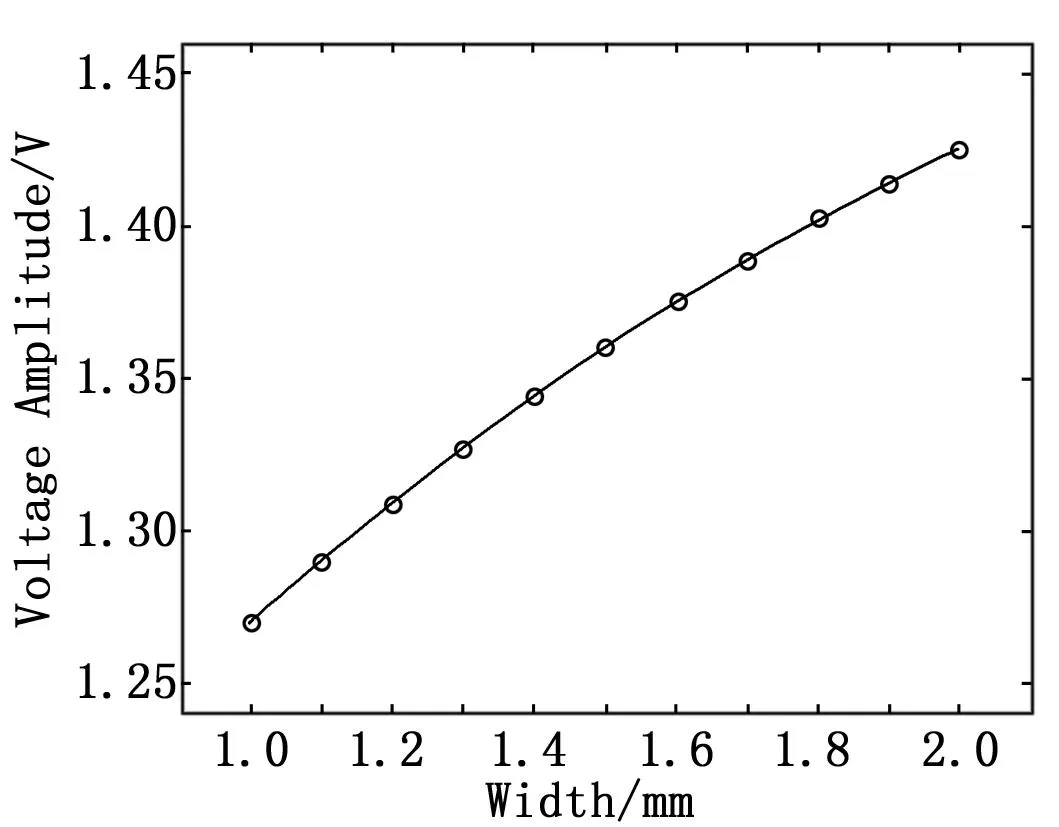
图8 不同微带线宽度的终端电压
保持其他参数不变,仅改变微带线的长度,计算微带线长度从40 mm到50 mm的终端电压,从结果可以看出,微带线的终端电压随着微带线长度的变长而逐渐增大,这是由于微带线长度的变长导致线上的等效激励源变大,从而使得终端电压变大。终端电压随着微带线长度变化的增长幅度为0.5 V,可见微带线长度对耦合效应具有较大的影响。
保持其他参数不变,仅改变微带线的宽度,计算微带线宽度从1 mm到2 mm的终端电压。从结果可以看出,微带线的终端电压随着微带线宽度的变宽而逐渐增大,终端电压随着微带线宽度变化的增长幅度为0.16 V,可见微带线宽度对耦合效应的影响相对较小。

图9 不同介质基板厚度的终端电压


图10不同介质基板材料的终端电压
保持其他参数不变,仅改变微带线介质基板的厚度,计算微带线介质基板厚度从1 mm到3 mm的终端电压,从结果可以看出,微带线的终端电压随着介质基板厚度的增加而逐渐增大,这与传输线间距越大耦合越强的规律一致。终端电压随着微带线介质基板厚度变化的增长幅度为0.07 V,可见微带线介质基板厚度对耦合效应的影响相对较小。
保持其他参数不变,仅改变微带线介质基板的材料,计算介质基板材料相对介电常数从2.2到3.6的终端电压,从结果可以看出,微带线的终端电压随着介质基板材料相对介电常数的增大而逐渐增大。终端电压随着微带线介质基板材料变化的增长幅度为0.03 V,可见微带线介质基板材料对耦合效应的影响相对较小。
3结论
本文采用线天线Pocklington积分公式和混合S参数方法计算了微带线在入射波和集总电源共同激励下的终端响应,所得结果和HFSS仿真结果基本吻合,利用此方法可以大大减少计算量,且能较为清晰的表示不同参数对耦合效应的影响。研究表明:微带线长度越长,宽度越宽,介质基板厚度越厚,介质基板材料的相对介电常数越大则入射波对微带线的耦合效应越强,其中,微带线长度对耦合效应的影响最为显著。
参考文献:
[1] Erdin I, Nakhla M S, Achar R. Circuit analysis of electromagnetic radiation and field coupling effects for networks with embedded fullwave modules[J]. IEEE Transactions on Electromagnetic Compatibility, 2000, 42(4):449-460.
[2] Besnier P, Chabane S, Klingler M. Some limiting aspects of transmission line theory and possible improvements[J]. IEEE Transactions on Electromagnetic Compatibility, 2014, 2(3):66-75.
[3] Poljak D, Antonijevic S.Drissi K E K, Kerroum K. Transient Response of Straight Thin Wires Located at Different Heights Above a Ground Plane Using Antenna Theory and Transmission Line Approach[J]. IEEE Transactions on Electromagnetic Compatibility, 2010, 52(1):108-116.
[4] Lapohos T, Joe L V, Joe S. External field coupling to MTL networks with nonlinear junctions: numerical modeling and experimental validation[J]. IEEE Transactions on Electromagnetic Compatibility, 2000, 42(1):16-28.
[5] Leone M, Singer H L. On the Coupling of an External Electromagnetic Field to a Printed Circuit Board Trace[J]. IEEE Transactions on Electromagnetic Compatibility, 1999, 41(4): 418-424.
[6] 彭强,周东方. 微带线的电磁耦合特性分析及实验验证[J]. 信息工程大学学报, 2013,14(1): 36-41.
[7] Frederick M T. Development and Use of the BLT Equation in the Time Domain as Applied to a Coaxial Cable[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 49(1): 3-11.
[8] Bayram Y, Volakis J. Hybrid S-parameters for analysis of mixed RF-digital circuits subject to external electromagnetic interference[J]. IEEE Transactions on Electromagnetic Compatibility, 2005, 47(2): 234-246.
[9] Bayram Y, Volakis J L. Hybrid S-Parameters for Transmission Line Networks With Linear/Nonlinear Load Terminations Subject to Arbitrary Excitations[J]. IEEE Transactions on Microwave Theory and Techniques, 2007, 55(5): 941-950.
[10] 林荣升.辐射电磁干扰对微波有源电路影响的研究[D].南京:南京航空航天大学, 2012.
[11] Chatterjee A, Volakis J L, Kent W J. Scattering by a perfectly conducting and a coated thin wire using a physical basis model[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(7): 761-769.
[12] 廖承恩. 微波技术基础[M].西安: 西安电子科技大学出版社,1994.
Investigation on Coupling Effect of Microstrip Line based on Hybrid S-parameters
Han Shuaitao1,2,Hou Deting1
(1.College of Science, Information Engineering University, Zhengzhou450001,China;2.Unit 63880,Luoyang471000,China)
Abstract:A hybrid S-parameter is used to study the terminal response of microstrip line subject to arbitrary plane wave and port excitations. The forced wave and modal wave are calculated by Galerkin’s solution. Compared with traditional method GPOF, It greatly improve the computational efficiency. Correctness of this method is validated by the comparation with the full-wave simulate software HFSS. The influence of different parameters on the microstrip line terminal was investigated using the hybrid S-parameter method. The results show that, the coupling effects will be stronger when the microstrip line is longer, wider, thicker and the relative permittivity is biger, and the influence of longitude is strongest.
Keywords:electromagnetic coupling; transmission line theory; hybrid S-parameters; printed circuit board(PCB)
文章编号:1671-4598(2016)02-0162-04
DOI:10.16526/j.cnki.11-4762/tp.2016.02.044
中图分类号:O441
文献标识码:A
作者简介:韩帅涛(1988-),男,河南汝州人,硕士在读,主要从事电磁兼容和高功率微波技术方向的研究。侯德亭(1963-),男,河南洛宁人,教授,主要从事高功率微波技术方向的研究。
收稿日期:2015-07-15;修回日期:2015-08-24。
