一种基于单位四元数的四旋翼编队反演控制方法

李　磊，李小民，杨　森

(军械工程学院 无人机工程系，石家庄　050000)



一种基于单位四元数的四旋翼编队反演控制方法

李磊，李小民，杨森

(军械工程学院 无人机工程系，石家庄050000)

摘要：针对四旋翼无人飞行器，研究了在理想通信条件下编队控制问题;四旋翼无人飞行器具有复杂的数学模型，首先用四元数描述其动力学和运动学模型，将其分解为位置和姿态两个相互独立的子系统，通过引入与期望轨迹之间的误差建立了跟踪误差模型；指定编队中一名成员为领航者，编队成员通过一致性算法得到编队的几何中心位置，并以此作为期望轨迹;通过Backstepping方法为每一架四旋翼设计时变反馈控制律使编队达到镇定；最后通过仿真实验验证该控制方法的有效性。

关键词：编队控制； 四旋翼无人机； 四元数； 反演法； 领航跟随法

0引言

近年来，小型无人机发展迅猛，四旋翼无人飞行器由于结构简单、易于控制，受到研究者们的广泛关注。四旋翼无人机能够实现垂直起降、自主悬停等功能，在不确定环境以及危险环境中能够高效的执行任务。无人机编队通过多无人机的协同飞行使系统的综合效能大大提高。随着任务日趋复杂，无人机数量逐渐增多，对编队控制提出了更多更高的要求。无人机编队控制是多无人机协同控制的重要研究方向。

编队控制的研究方法主要有领航跟随法、虚拟结构法、基于行为法和图论法[1]。目前较为主流的是将上述方法融合使用，取长补短。早期的编队控制主要采用集中式控制方法，其特点是精度高、便于控制，但是要依赖于中央控制单元的计算能力和全局通信能力，随着编队成员的增加，中央控制单元的计算量呈指数增加，缺乏可拓展性和灵活性。后来人们提出分布式控制方法，每架无人机只与相邻的无人机进行通信，利用无人机自身的计算能力，得到周边无人机的相对位置关系，对比期望的编队队形，对无人机的实际位置进行修正进而消除队形误差。

近年来，国内外诸多学者针对四旋翼飞行器编队问题做了大量研究[2-5]，设计出不同类型的控制器。文献[2-5]通过反馈线性化、小扰动线性化等方法对四旋翼飞行器模型进行了不同程度的简化来设计控制器。但是四旋翼飞行器是一种典型的欠驱动系统，是具有复杂约束方程的级联非完整系统[7],具有很强的非线性，对控制系统提出了更高的要求。文献[6]同样采用单位四元数对四旋翼进行建模，并且引入流形的概念，在微分几何框架下设计了姿态控制算法，取得了不错的效果。文献[7]利用神经网络在线辨识系统的非线性部分，结合领航跟随法实现了四旋翼的编队控制。文献[8]用四元数描述四旋翼的动力学和运动学模型，引入中间控制量，通过为每一架无人机设计合适的中间控制量使得编队达成镇定。文献[9]引入实际位姿与期望位姿间的误差，建立了跟踪误差模型，并将四旋翼模型分解为位置和姿态两个互相独立的子系统，并分别利用Backstepping方法设计了时变反馈控制律使系统稳定。Backstepping方法是一种由前向后递推的设计方法，通过逐步迭代设计Lyapunov函数使系统误差具有渐进性，并使系统最终实现全局稳定，降低了设计难度。本文在文献[9]的基础上，通过一致性算法得到编队几何中心位置，并将其作为期望轨迹，为每一架四旋翼设计反演控制律使整个编队达到镇定。

1单位四元数基础

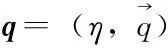
单位四元数是模恒为一的四元数，即有

(1)

给定一个单位四元数，其对应的姿态矩阵与单位四元数之间有如下关系：

(2)

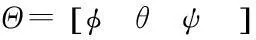
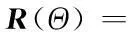
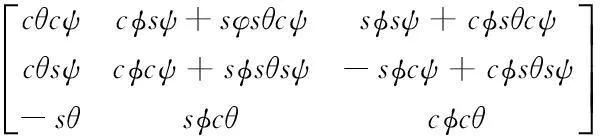
(3)

定义实际姿态矩阵R与期望姿态矩阵Rd间的误差为

(4)

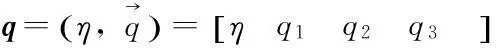
(5)

2四旋翼系统原理及模型

四旋翼无人机通常分为“X”型和“+”型，具有4个输入6个输出，是典型的欠驱动系统。四旋翼通过控制4个独立的电机和螺旋桨的转速来实现飞机的升降、俯仰、滚转和偏航等运动。四元数是描述三维空间中刚体转动和移动的简洁有效的数学工具，可以有效避免奇异点的出现，并且具有计算高效等特点。将四旋翼无人机看做刚体结构，假设其重心位于机体坐标系原点，电机无安装误差角，且电机升力面与飞机质心位于同一平面。利用四元数对四旋翼动力学和运动学建模，将四旋翼分解为位置子系统∑1和姿态子系统∑2，得到以下模型：

(6)

(7)

3控制器设计及收敛性分析

3．1问题描述

考虑无人机编队有N+1个成员,指定编号为1的无人机为编队领航者。假设每架无人机都可以通过自身的传感器和无线通信网络获取自身和编队其他成员的状态信息。根据无人机之间信息交互关系可以将无人机编队建模成图的形式。假设无人机通信拓扑图为无向连通图，如图(1)所示，在编队开始时，各编队成员通过无线通信网络获取自身和编队其他成员状态信息后，通过一致性算法协商得出编队期望的位置中心和期望速度，并将其输出到位姿控制器，驱动执行元件使无人机向预定编队中心靠拢聚集，达到指定间距后，完成编队任务。

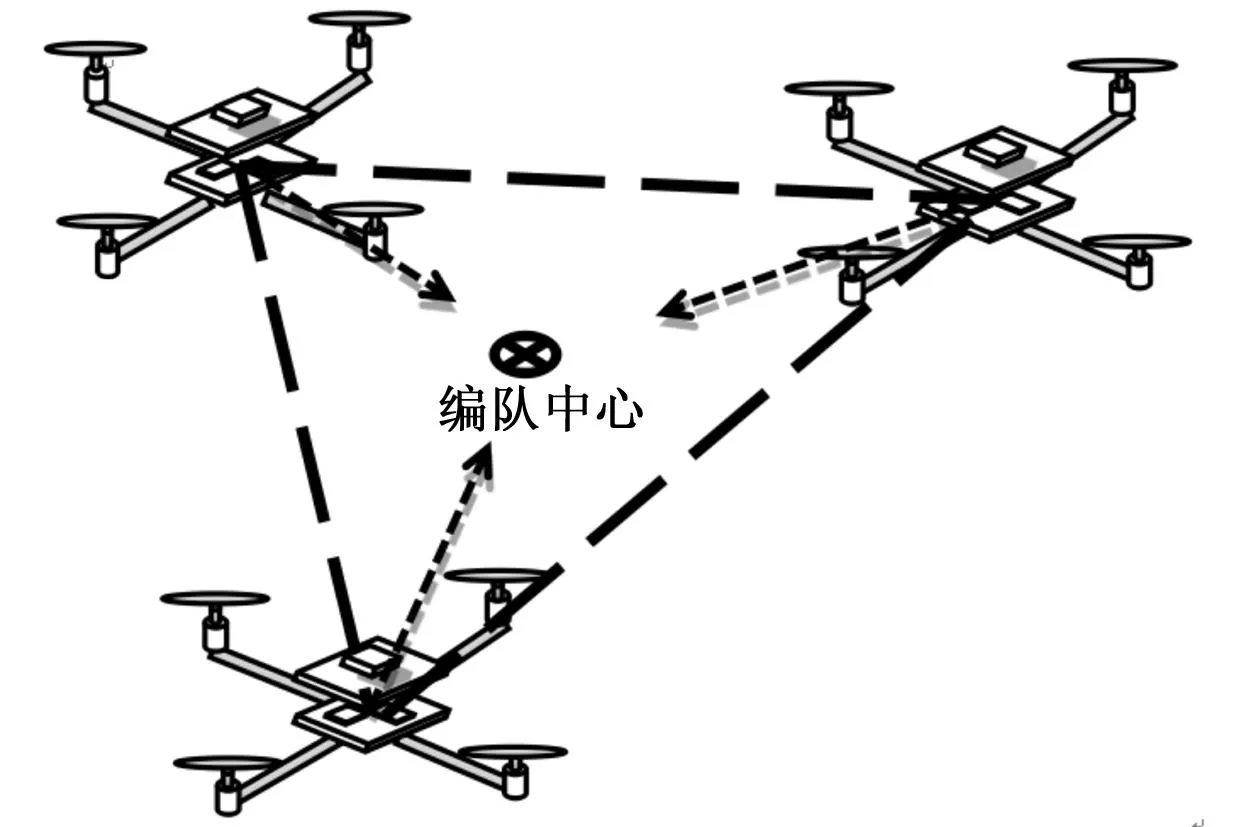
图1　四旋翼编队示意图

不考虑编队中的四旋翼的差异性，即四旋翼为同构系统，且都符合模型(6)，即

(8)

(9)

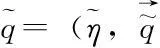
(10)

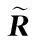
(11)

本文要做的工作是为第i架四旋翼无人机设计虚拟控制量升力Ti和控制力矩τi，使四旋翼编队保持固定队形和固定距离，即使得

vi→vj→vd，且ξi-ξj→δi-δj=δij

式中vd为编队参考的期望速度，δij为第i架无人机和第j架无人机之间的期望距离，并且满足δij=-δji。

3．2控制器设计

根据级联系统分析方法将四旋翼误差系统模型分解为位置误差子系统和姿态误差子系统[10]

(12)

(13)

下面参考文献利用BackStepping方法分别设计位置子系统控制器和姿态子系统控制器.

首先，定义系统状态与虚拟反馈之间的误差

(14)

式中，α1为虚拟控制量。现对每一个虚拟反馈定义一个V函数，使每一个状态分量具有适当的渐进性，式(14)本质上是一个微分同胚，为了镇定原系统，只需镇定原系统状态与虚拟反馈量之间的误差即可。

第1步：对z1求时间导数，得

(15)

(16)

显然，如果z2=0，由上式知z1渐进稳定，但一般情况下z2≠0，为此需要进行下一步设计，使z2具有期望的渐进特性。

V2关于时间的导数为:

(17)

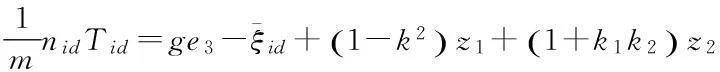
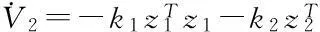
(18)

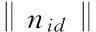
利用同样的方法为姿态子系统设计控制律使其全局指数稳定，定义姿态子系统系统状态与虚拟反馈之间的误差

(19)

其中：α2为虚拟控制量。

编队控制中主要关心飞行器的位置控制子系统。因此，下面直接给出四旋翼无人机i的姿态子系统反演控制律，具体推导过程参考文献[10]。

(20)

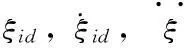
(21)

(22)

这就将编队问题转化成给定参考信号的轨迹跟踪问题，式中Ni为编队中与第i架无人机为邻居的飞行器的数量。考虑编队通信拓扑为无向全通图时的情形，此时除领航者外，编队中任意飞行器具有同等地位，因此可以忽略下标i，将式(21)和式(22)改写成如下形式：

(23)

通过反演控制律可以保证编队中第i架无人机ξi→ξd+δi，vi→vd，则可以保证ξi-ξj→δi-δj=δij，vi→vj。

4实验仿真

4．1参数设置

不考虑四旋翼系统之间存在的差异，假设系统质量m=0．6 kg，转动惯量分别为Jx=Jy=0．2 kg·m2，Jz=0．04 kg·m2。设置编队规模N=5，k1=10，k2=10，指定编号为5的四旋翼为领航者，其余四架为跟随者，假设领航者向外广播自身的状态信息，跟随者均能实时接收，并且跟随者之间的通信拓扑为无向连通图。跟随者初始位置矩阵P0为:

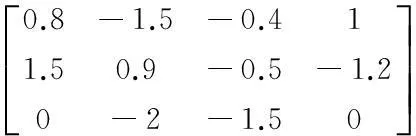
领航者在固定高度做匀速圆周运动，其运动轨迹为：

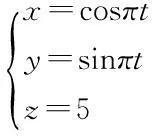
用来描述编队队形的相对位置偏差为:

仿真时间为9．5s，仿真步长为0．001s。

4．2仿真结果

根据以上参数，用MATLAB中Simulink模块搭建系统模型，并对控制算法进行验证。图2为编队仿真的三维轨迹图。图中黑色曲线为领航者的运动轨迹，三角形“△”表示每架四旋翼无人机的最终位置。仿真开始时，领航者在空中做圆周运动，跟随者在地面的不同位置，起飞后接收领航者的状态信息，首先编队成员通过协商计算得到编队中心位置，并以此作为参考跟踪信号，算法式(18)最终使五架四旋翼收敛至预定编队队形。通过设置不同的相对位置误差可以方便地设计各种队形。

图2　四旋翼编队轨迹仿真曲线

图3　X方向无人机位置与速度变化曲线

图3~图5分别从XYZ三个方向显示了机群成员在编队形成和机动过程中位置和速度的变化规律。从图中可以看出，跟随者在起飞后迅速向领航者靠拢，在t=1s时跟随者距离领航者趋于指定位置，并且与领航者保持相同的速度，能够很好地跟踪领航者的轨迹变化，验证了本文所提编队策略的有效性。

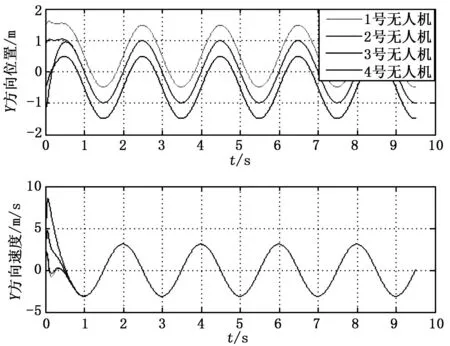
图4　Y方向无人机位置与速度变化曲线

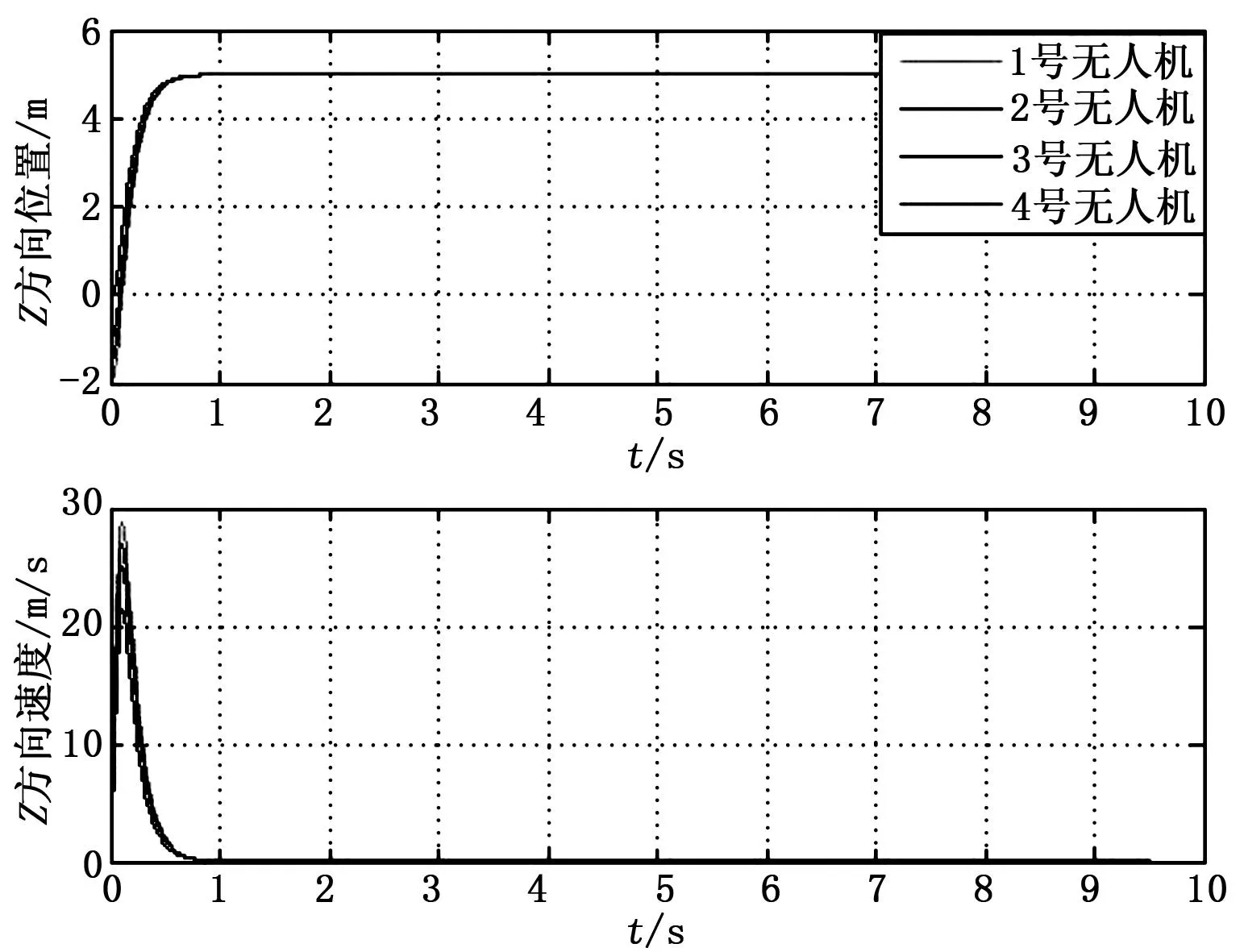
图5　Z方向无人机位置与速度变化曲线

图6为编队成员协商计算得出的编队中心轨迹与领航者轨迹之间的误差，可见，编队中心最终收敛于领航者所在位置。

图6　参考轨迹与领航者轨迹误差

5结论

针对四旋翼无人飞行器编队控制问题，用单位四元数描述其非线性动力学模型和运动学模型。采用跟踪编队几何中心的方法实现编队控制。编队开始时编队成员通过无线网络交换位置、速度等状态信息，计算协商得出编队几何中心，并以此作为参考信号，通过Backstepping方法为每一架无人机设计了时变反馈控制律，这将编队问题转化为给定参考信号的跟踪问题，通过MATLAB仿真检验了该方法在大角度快速机动时的有效性，仿真结果表明该方法计算速度快、精度高，提高了编队系统收敛速度。目前方法尚未考虑朝向一致问题和包含最大速度约束下的编队问题，后续研究将考虑朝向一致以及在最大速度约束等约束条件下设计编队生成、保持及重构方法。

参考文献：

[1] 王祥科,李迅,郑志强. 多智能体系统编队控制相关问题研究综述[J]. 控制与决策,2013,28(11): 1601-1613.

[2]F.Rinaldi,S.Chiesa,F.Quagliotti.LinearQuadraticControlforQuadrotorsUAVsDynamicsandFormationFlight[J].IntellRobotSyst. 2013(70):203-220.

[3] 夏梁盛.基于集群的多机器人编队控制[J].火力与指挥控制，2013,38(1)：18-21.

[4]YuBC,DongXW,ShiZY,etal.Formationcontrolforquadrotorswarmsystems:Algorithmsandexperiments[A].Proceedingsofthe32ndChineseControlConference[C],26-28,July2013,xi’anChina.

[5]ChoiInSung,ChoiJongSuk.Leader-FollowerFormationControlUsingPIDController[A]. 5thInternationalConference[C],3-5,October,2012,Montreal,Canada.

[6] 安宏雷,李杰,马宏绪,等.基于单位四元数的四旋翼无人直升机几何控制[A].第24届中国控制与决策会议论文集[C].2012.

[7]DierksT,JagannathanS.NeuralnetworkcontrolofquadrotorUAVformations[A].AmericanControlConference[C].St.Louis,USA. 2009.

[8]AbdessameudA,TayebiA.FormationcontrolofVTOL-UAVs[A].Joint48thIEEEConferenceonDecisionandControland28thChineseControlConference[C]. 2009.

[9] 李光春,王璐,王兆龙,等.基于四元数的四旋翼无人飞行器轨迹跟踪控制[J].应用科学学报，2012,30(4):415-422.

Formation Control of Quadrotors with Unit Quaternions Based via Backstepping Method

Li Lei, Li Xiaomin, Yang Sen

(Department of UAV Engineering，Ordnance Engineering College，Shijiazhuang050000，China)

Abstract:Formation control under ideal communication conditions is studied for quadrotor UAV. The quadrotor UAV has complex mathematical model. First of all, the quadrotor is decomposed into two independent subsystems of position and attitude by the quatenion describing its dynamics and kinematics model. The tracking deviation model is estabilished by introducing deviation of the expect track. One member in the formation is specified as leader. By consencus algorithm the fleet gets through the geometric center as the expect track. A time varying feedback control law that making formation stabilization is designed for each quadrotor with BackStepping method. Finally, the effectiveness of this algorithm is showed through the simulation results.

Keywords：formation control; quadrotor; quaternion; backstepping; follower-leader

文章编号：1671-4598(2016)02-0064-04

DOI：10.16526/j.cnki.11-4762/tp.2016.02.017

中图分类号：TP242.6

文献标识码：A

作者简介：李磊(1990-)，男，河北宁晋人，硕士研究生，主要从事无人机测控与飞行控制技术方向的研究。李小民(1968-)，男，河北保定人，教授，博士生导师，主要从事导航与控制及无人机运用技术方向的研究。

基金项目：“十二五”国防预研项目(51325050101)。

收稿日期：2015-07-17；修回日期：2015-08-27。