浅谈培养初中生的数学学习反思习惯
2016-03-17福建省泰宁县第四中学邱晓燕
福建省泰宁县第四中学 邱晓燕
浅谈培养初中生的数学学习反思习惯
福建省泰宁县第四中学 邱晓燕
在教学活动中,只有培养学生的学习反思习惯,才能提高学生的学习能力.引导学生在学习新知识的过程中养成反思习惯;在解题探究活动中养成反思习惯;在拓展探究活动中养成反思习惯,促使学生养成反思的好习惯.
学习反思 解题反思 初中数学
数学是一门抽象性较强的学科.在学习过程中学生的自我意识对其学习的效果和质量有着非常重要的影响.目前,“题海战术”依然是数学学习的主要方式,这种方式暴露出两个问题:(1)在数学知识的形成过程中,学生没有反思,造成对概念理解不透彻的后果;(2)在知识的应用过程中,学生没有养成解题后反思的习惯,特别是错题后反思错误的习惯,造成“一听就懂,一做就错”的现象.所以,教师在教学过程中应运用各种方式引导学生进行反思,从而增强学生对学习的反思意识和能力.
一、在学习新知识的过程中培养学生的反思习惯
数学课程标准明确指出“养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯,形成实事求是的科学态度”.因此,在新知识的学习过程中应注重培养学生的反思习惯.
数学中有很多概念、性质、定理都具有相似的属性.对这些具有相似属性的知识教学,教师应当引导学生反思已学过的知识的属性,通过类比、分析、归纳,让学生在反思中形成清晰的数学知识.
例如,我们在学习《一次函数》时,学习了一次函数的定义;用待定系数法求函数解析式;研究图像的方法;研究图像的性质从图像经过的象限与增减性方面着手.那么在学习《反比例函数》与《二次函数》时,可以类比一次函数来研究,反思一次函数相关知识内容,更重要的是反思研究一次函数的方法;通过反思、横向类比,深化概念,从知识结构的角度把握一次函数、反比例函数、二次函数的定义与性质,建立知识结构网络.
数学概念之间存在着紧密的联系,通过反思建立知识间联系的纽带,加强了知识间的对比,从而形成清晰的知识网络.
二、在解题探究活动中应引导学生反思解决问题的思维过程,养成反思习惯
1.对解题思路的反思.
在解题教学活动中,要先引导学生反思解决问题的思路,用已学的方法研究新问题,使学生在反思中探索新知识的解题方法,从而提高解决问题的能力.
例1.以△ABC的两边AC、BC向外做正方形ACFD和正方形CGEB,分别过点D、E作DD1⊥直线AB,EE1⊥直线AB,垂足分别为D1、E1.

图①

图②
(1)当点E在直线AB上时(如图②),求证DD1=AB;
(2)当E、D两点都在直线AB的上方时(如图①),求线段DD1、EE1、AB之间的数量关系;
(3)当点E在直线AB的下方时(如图③),求三条线段DD1、EE1、AB之间的数量关系.
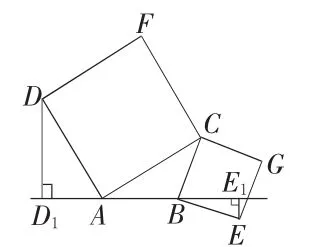
图③
引导学生反思要证明DD1=AB就必须证明什么?学生证出(1)后,引导学生反思没有全等三角形怎么办?(构造全等三角形)做CH垂直AB,垂足为H,可以证得△ADD1≌△CAH,即可得DD1=AH,同理EE1=BH,则可得AB=DD1+EE1.再引导学生反思(3)与(2)的异同点,抓住变与不变的量,总结得到:图形变化了,证明三角形全等的依据不变,最后的结论发生了细微的变化.
以上通过引导学生反思探究问题的整个思维过程,使其形成探索新知的方法.
2.对错误原因的反思.
对错误原因的反思,不仅能及时纠正学生的错误,更能深化学生对知识、技能的理解,做到提高学习效率.
例题:解方程(x-2)(x-1)=x-1
很多学生的答案如下:
解:等式两边同时除以(x-1)得x=2
我们定要引导学生反思:等式两边同时除以一个数的条件是什么?题目给的条件符不符合?漏根的原因是什么?解题后引导学生反思错误,找到“病根”,今后学生对运用等式基本性质解题就不会再犯相同的错误.
三、在拓展探究活动中养成反思习惯
在知识的应用过程中,我们习惯采用“模仿训练”.解题后没有及时引导学生进行反思拓展,导致同一种问题,稍微改变部分已知条件、或是已知条件不变仅仅改变图形、或是改变结论,学生就解不出来.因此,教师应重视加强学生在拓展探究活动中养成反思习惯,提高学生的探究能力.
1.对知识点联系拓展的反思.
例2.抛物线y=ax2-3x-4的图像与y轴交于A点,x轴交于B、C两点,已知B点坐标为(-1,0),求此抛物线的解析式.
解题后,学生通过反思,总结出函数解析式只有一个待定系数,只需将一个点坐标代入解析式中即可.此时可以拓展出第二个问题:若点P是位于直线AC下方抛物线上的点,求△PAC的面积的最大值,并求出此时P点的坐标.
引导学生反思联系:△PAC中,边AC的长度是定值,要使△PAC面积最大,只需以AC为底的高h最大即可.要使h最大,则点P到AC的距离最大,因为P在抛物线上,所以当平行于AC的直线与抛物线有且只有一个交点时,h取最大值,此时△PAC面积最大.
拓展反思可以使学生在记忆里孤立的知识“点”,不断扩展成系统的知识“面”.通过不断地拓展、反思,学生对知识的理解会逐渐系统化.
2.对数学规律的拓展反思.
例3下列选项中,阴影部分面积最小的是( ).

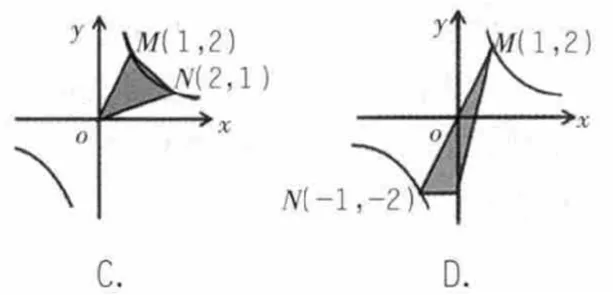
解题后引导学生反思规律,即在反比例函数的图像上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是且保持不变。拓展到反比例函数的图像上任意一点向坐标轴作垂线,与坐标轴围成的矩形面积为进而可以拓展到根据图形求k的取值范围.学生通过对规律的拓展反思,学会由特殊规律引申出一般规律,不仅强化了知识的运用,还提高了迁移水平.
3.对数学思想的拓展反思.
这样就可以看成y是坐标系中一动点(x,0)到两点(0,3)和(4,1)的距离之和,于是本问题转化为求最短距离问题.
解题后,要引导学生反思:“数”与“形”主要有以下两个结合点:(1)利用数轴、坐标系把几何问题代数化;(2)利用面积、距离、角度等几何量来解决几何问题.例如:利用勾股定理证明直角、利用三角函数研究角的大小、利用线段比例证明相似等.
对数学思想的拓展反思,避免了学生只会解老师讲解过的题目,一旦出现“新面孔”就无从下手.
4.对一题多解的拓展反思.
解题教学中我们常会引导学生反思:解法是否唯一?你的解法是否最简便?通过反思提高学生的思维的灵活性,掌握从多角度解题的方法.
5.对一题多变的拓展反思.
对一题多变的拓展反思,不仅可以加深学生对问题结构和特征的理解,而且有利于学生思维的广阔性的培养,使学生“知一题,懂一串”,达到“能快速解决没有见过的题目”的高度.
例如:求证:顺次连结四边形各边中点所得的四边形是平行四边形.一般学生解决这个问题是不困难的,于是我再加以引申,引导学生从以下角度反思:把四边形改成梯形→矩形→菱形→正方形,得到的中点四边形是什么图形?而后再进行拓展:中点四边形是矩形,原四边形必须满足什么条件?菱形呢?正方形呢?
这样一系列变式反思,学生就能掌握《四边形》这一章基础知识和基本概念,理顺了不同四边形的内在联系,为进行数学问题演变奠定了扎实的知识基础.
学习数学不仅仅是获得知识,还要注重深层次的情感态度价值观.反思不仅能深化对知识的形成过程的理解,提高解题的能力,更能培养学生科学的学习态度.因此,教师要将反思习惯的培养渗透到教学的各个环节中,去帮助学生形成良好的反思习惯,它对学生的一生发展都有重大意义.
