海洋重力仪采样质量悬挂系统分析
2016-03-16高贤志赵晶睛乔立伟
高贤志,杨 稳,于 浩,赵晶睛,乔立伟
(1.海军驻天津地区某所军事代表室,天津 300131; 2.天津航海仪器研究所,天津 300131)
海洋重力仪采样质量悬挂系统分析
高贤志1,杨 稳2,于 浩2,赵晶睛2,乔立伟2
(1.海军驻天津地区某所军事代表室,天津 300131; 2.天津航海仪器研究所,天津 300131)
针对轴对称型海洋重力仪采样质量悬挂系统的刚度设计问题,运用材料力学和最小势能原理重点对水平和垂直方向的等效刚度进行理论分析,分析结果表明:系统在水平面内各方向的刚度相等,与拉丝材料的弹性模量和横截面积成正比,与拉丝的初始长度成反比;系统竖直方向等效刚度与绷紧弹簧的张力成正比,与拉丝的初始长度成反比。对仪器工程应用中,因拉丝弯曲而产生的干扰阻力进行了评估分析,结果表明在正确选择拉丝的材料和几何尺寸的条件下,由干扰阻力所引起的误差可以忽略不计。
海洋重力仪;采样质量悬挂系统;等效刚度
0 引言
当前广泛应用的零长弹簧海洋重力仪主要有摆杆型和轴对称型两种工作方式,其中轴对称型海洋重力仪在测量时不受水平加速度的影响,从理论上消除了交叉耦合效应的误差,能在较恶劣海况下工作。
轴对称型海洋重力仪基于直线弹簧拉伸原理设计。工作时采样质量悬挂系统会改变弹性系统在垂直方向的刚度,这将会对重力仪中的灵敏度产生很大影响,故必须对其结构进行精确的分析和计算[1]。
1 采样质量悬挂系统的结构
在采样质量悬挂系统中,为了便于安装拉丝与绷紧弹簧,通常将采样质量做成管状。管状质量由轻质合金制成并悬挂在垂直安置的主弹簧下端,水平拉丝和绷紧弹簧用来约束管状质量的5个自由度,使其只能沿轴线方向运动。在实际工程应用中,由于拉丝和绷紧弹簧刚度不同,管状质量在上下运动的同时还伴有轻微转动,但这种情况对仪器的测量精度影响不大。为了限制采样质量的5个运动自由度,至少需要5根拉丝。但5根拉丝与绷紧弹簧的位置不是轴对称的,在恶劣的海况下工作时,采样质量常受到不同方向的振动和冲击,不对称的拉丝分布可能会引起采样质量运动轨迹的扭曲,从而影响仪器的精度。所以一般采用6根拉丝悬挂系统,其原理结构如图1所示[2]。
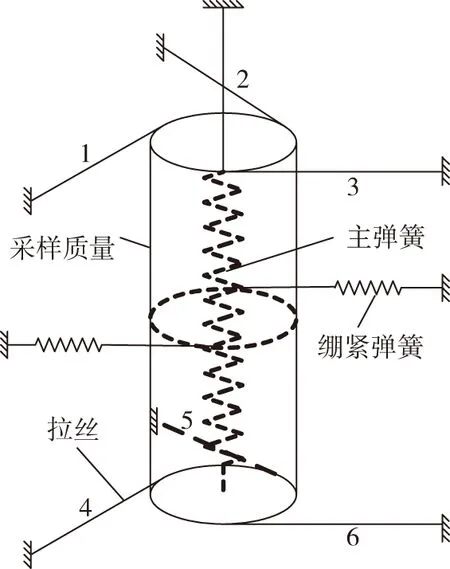
图1 6根拉丝悬挂系统结构示意图Fig.1 Diagram of the suspension system with six wires
6根拉丝沿着采样质量的外表面的切向固定,每3根为1组,互成120°,分布在上、下两个水平面内。为拉丝提供张力的2根绷紧弹簧位于中间平面,并互成180°。全部拉丝和绷紧弹簧的外端点均用压片固定在弹性系统的壳体上,这样管状质量只能沿其轴线方向平移。从整体布局来看,该悬挂系统无论是拉力、应力还是拉丝与绷紧弹簧的分布位置都相对于采样质量的轴线对称,其沿任意水平方向的刚度都是相等的,因而采样质量的运动比较平稳,有利于进一步提高仪器的抗干扰能力[3]。
2 采样质量悬挂系统计算分析
2.1 系统水平方向刚度的计算分析
采样质量的受力情况如图2所示,其中O为采样质量的质心。它受到的水平方向的作用力有6根拉丝的张力F1、F2、F3、F4、F5、F6,绷紧弹簧的拉力P以及水平干扰力H。垂直方向的作用力有采样质量的自重G和主弹簧的拉力T。所有这些力组成一个空间非汇交力系,为了方便计算,可以将所有水平方向作用力的作用点均移到采样质量的轴线上,这样每根拉丝的切向力就变成了作用在轴线上的水平拉力和绕轴线转动的附加力偶[4]。
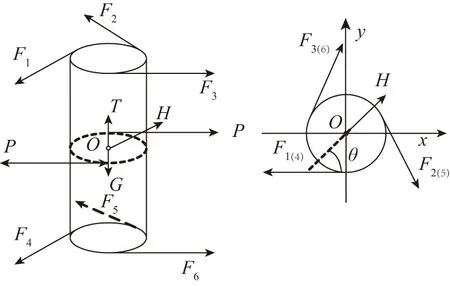
图2 采样质量受力示意图Fig.2 Force diagram of sampling mass
当系统不受水平干扰力的作用(即H=0)时,由受力分析可知所有拉丝中的拉力都相等,可以将其设为F0,另外根据力矩平衡可知F0=P/3;当系统受水平干扰力的作用(即H≠0)时,采样质量会在水平方向上产生微小位移,每根拉丝的长度和绷紧弹簧的长度也会有微小变化,但绷紧弹簧的刚度远小于拉丝,可以认为拉力P在此过程中保持不变。假设重心O的位移为Δ,由几何关系可知各拉丝长度的变化量:
(1)
式中,θ为水平干扰力H与拉丝1、4所在竖直平面的夹角(见图2),因为结构的对称性,故仅需要考虑0≤θ≤60°时的情况。
此时各拉丝中的张力也会发生变化,根据胡克定律可知其值如下:
(2)
式中:E为拉丝材料的弹性模量;A为拉丝的横截面积;L0为拉丝的初始长度。
首先运用理论力学的知识对该结构进行分析。由于系统结构具有对称性,可单独对相同水平面内的3根拉丝进行分析,由受力平衡可知:
(3)
将式(2)代入式(3)并进行化简,可得到:
(4)
因为cosθ与sinθ不可能同时为零,所以
(5)
进而得到系统在水平面内的等效刚度
(6)
为了验证上述推导的正确性,以下运用最小势能原理对该结构进行重新分析,各拉丝中应变能的变化量为[5]:
(7)
水平干扰力H所做的功
W=HΔ
(8)
悬挂系统的总势能为
(9)
当系统取最小总势能时有
(10)
由此可得到,系统在水平面内的等效刚度为
(11)
经过以上两种方法分析都可以得到:图2中所采用的结构在任意水平方向的刚度都是相等的,并且与拉丝材料弹性模量E和拉丝横截面积A成正比,与拉丝的初始长度L0成反比。
2.2 绷紧弹簧初始张力的选择
在计算水平刚度后,还需要对绷紧弹簧的初始张力进行分析计算。由于拉丝属于非刚体,只能承受拉力而不能承受压力,那么为使采样质量平稳地运动,每根拉丝中的张力必须不小于零。即:
其中:0≤θ≤60°,F0=P/3。
将式(1)带入式(12),可以得到:
(13)
那么可以知道
(14)

P≥0.15N
(15)
即在0.15N的情况下,弹性系统能够在500Gal水平扰动加速度的作用下正常工作(在实际的设计中还应考虑到足够的安全系数)。
2.3 系统在竖直方向等效刚度的计算分析
当采样质量位于零位时,全部拉丝以及绷紧弹簧都与主弹簧垂直,它们的拉力在竖直方向没有分量,因而在竖直方向上不会对采样质量产生作用。当采样质量偏离零位时,破坏了这种相互垂直的关系,主弹簧和全部拉丝、绷紧弹簧在垂直方向上对采样质量共同起作用,这样就改变了弹性系统在竖直方向的刚度,同时亦改变了它的灵敏度。在此要对这种情况进行分析和计算。
假设采样质量的轴向位移为δ,其受力情况如图3所示。由结构的对称性可知各拉丝中的张力相等,并且拉丝和绷紧弹簧与水平面的夹角也相等,则拉丝和绷紧弹簧张力在竖直方向上的分量为

图3 采样质量偏离零位受力示意图Fig.3 Force diagram of sampling mass when deviating from the zero position
Fv=6(F0+ΔF)sinα+2(P+ΔP)sinα
(16)
式中:α为拉丝和绷紧弹簧与水平面之间的夹角;F0为拉丝中的初始张力;ΔF为拉丝张力的变化量;P为绷紧弹簧的初始张力;ΔP为绷紧弹簧张力的变化量。
式(16)经过进一步整理可得
Fv=(6F0+2P)sinα+(6ΔF+2ΔP)sinα
(17)
由此可知,该分量由两部分组成:第一部分由初始张力产生,第二部分由形变产生。
由胡克定律可知,拉丝和绷紧弹簧中张力的变化量如下:
(18)
式中:E为拉丝材料的弹性模量;A为拉丝的横截面积;L为未发生位移时拉丝与绷紧弹簧的长度;L为发生位移后拉丝与绷紧弹簧的长度;K为绷紧弹簧的刚度。
那么,式(17)可化为
(19)
由二项式定理可知
(20)
因为,δ≪L0故略去二次以上的高次项得到
(21)
那么,式(19)可进一步化为
(22)
在重力仪正常量程范围内,式(22)的后一项远比前一项小得多,所以可近似认为
(23)
因为δ< (24) 那么拉丝和绷紧弹簧在竖直方向上的刚度为 (25) 在计算完Kv后,还要检验其对弹性系统等效灵敏度的影响。为满足电容测微器的灵敏度要求,弹性系统的等效灵敏度应大于0.01μm/mGal。取P=0.2N,L0=60mm,由式(25)可知Kv=13.3N/m,而主弹簧刚度Ks=3N/m,那么在采样质量偏离零位时,弹性系统的等效刚度Ke=Ks+Kv=16.3N/m。如果采样质量M=30g,则与此等效刚度相对应的仪器等效灵敏度为0.018μm/mGal。此参数选择恰当,符合设计要求。 2.4 干扰阻力的影响 在实际测量过程中,拉丝的干扰阻力也会对观测结果造成影响。拉丝产生干扰阻力的原因有两个:一是由拉丝本身具有的残余应力;二是当重力变化时,敏感质量沿其轴线的上下移动会引起拉丝和绷紧弹簧的弯曲,弯曲的拉丝就会对采样质量产生反作用力。对于第二部分干扰阻力,即因拉丝弯曲而产生的反作用力R,可用下述公式计算 (26) 由式(26)可知,反作用力与拉丝材料的弹性模量、横截面对中性轴的惯性矩、端点的位移量成正比,而与拉丝的初始长度成反比。取E=380GP,d=0.01mm,δ=0.1mm,L0=60mm,此时R=2.6×10-10N。若采样质量M=30g,那么2.6×10-10N相当于8.7×10-4mGal,由此看来,如果正确选择拉丝的材料和几何尺寸,由反作用力所引起的误差可以忽略不计。 在具体采样质量悬挂系统的设计过程中,拉丝参数和绷紧弹簧初始张力的选择对仪器性能有重大影响:拉丝长则非线性误差小、等效灵敏度高,但是拉丝过长会减小悬挂系统在水平方向的刚度,同时使得仪器过于笨重;拉丝越细,仪器的灵敏度越高,但是拉丝过细也会减小悬挂系统在水平方向的刚度,而且增加装配难度。绷紧弹簧的初始张力过小,在受到较大水平干扰力作用时,仪器无法正常工作;初始张力过大,弹性系统的等效刚度也会随着增大,这就提高了对电容测微器的要求。因此在进行设计时,应综合考虑上述因素,选取合理值。 本文针对轴对称型海洋重力仪中,采样质量悬挂系统的刚度问题,分别利用理论力学和最小势能原理两种方法进行了理论分析,并推导出了相应的刚度公式,根据公式得出6根拉丝的悬挂系统在任意水平方向的刚度相等,并与拉丝材料的弹性模量和拉丝的横截面积成正比,与拉丝的初始长度成反比;在竖直方向的刚度与绷紧弹簧的张力成正比,与拉丝的初始长度成反比。将相关设计参数代入公式验证,满足仪器的设计指标要求,这对海洋重力仪的研制有重要的工程参考价值。 [1] Chapin D. Gravity instruments: Past, present, future [J]. The Leading Edge, 1998, 17(1):100-112. [2] 刘若曾. CHZ海洋重力仪弹性系统的设计[J]. 测量与地球物理集刊, 1986(8):105-110. [3] 张善言. CHZ海洋重力仪的若干特点[J]. 测量与地球物理集刊, 1991(12):95-96. [4] 刘鸿文.材料力学(第4版)[M].北京:高等教育出版社, 2004 :33-43. [5] 金宝桢.结构力学[M].北京:人民教育出版社, 1958 :127-153. Analysis of the Suspension System of Sampling Mass in the Marine Gravimeter GAO Xian-zhi1,YANG Wen2,YU Hao2,ZHAO Jing-jing2,QIAO Li-wei2 (1.Military Representative Office of Navy in Tianjin Area, Tianjin 300131,China;2. Tianjin Institute of Navigation Instrument, Tianjin 300131, China) The horizontal and vertical stiffnesses of the sampling mass suspension in the axial symmetrical marine gravimeter system are mainly studied with material mechanics and the principle of minimum potential energy. The results show that, in the horizontal plane, the suspension system has in all directions the same stiffness which is proportional to the elastic modulus and cross sectional area of the wires, and inversely proportional to the initial length of the wires; the equivalent stiffness of the suspension system in vertical direction is proportional to the initial tension of the springs, and inversely proportional to the initial length of the wires. In engineering application, the interference resistance by curving of the wires is analyzed, the results show that, with rationally chosen materials and geometry dimensions of the wires, the error caused by the interference resistance could be negligible. Marine gravimeter; Suspension system of sampling mass; Equivalent stiffness 10.19306/j.cnki.2095-8110.2016.06.001 2015-03-30; 2015-05-18。 装备预先研究项目(51309040701) 高贤志(1978 - ),男,工程师,主要从事舰船导航方面的研究。 U666.1 A 2095-8110(2016)06-0001-05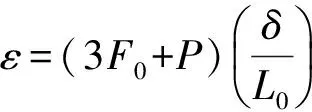
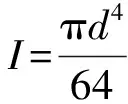
3 结论
