空空导弹SINS飞行中对准技术

周本川，鲁 浩，段朝阳

(中国空空导弹研究院 航空制导武器航空科技重点实验室，河南 洛阳471099)

空空导弹SINS飞行中对准技术

周本川，鲁 浩，段朝阳

(中国空空导弹研究院 航空制导武器航空科技重点实验室，河南 洛阳471099)

针对空空导弹捷联惯导系统传递对准的精度和快速性之间的矛盾，设计一种利用弹载北斗卫星导航信息的捷联惯导系统飞行中对准算法，详细推导了惯性系下基于北斗卫星伪距/伪距率的飞行中对准模型，优化了飞行中对准的量测方程，对北斗卫星接收机的钟差和钟漂进行了降维处理。相应的数学仿真试验结果表明，所提算法能够在飞行过程中实现捷联惯导系统的初始对准，在10s内对准精度优于6′，同时该算法通过在线标定惯性传感器随机启动误差，能够提高捷联惯导系统导航精度和导弹系统抗干扰能力。

飞行中对准；伪距/伪距率；在线标定

0 引言

空空导弹普遍装备捷联惯导系统用于导弹的中制导，初始姿态误差严重影响中末制导交接班精度。初始对准问题是弹载捷联惯导系统的关键技术之一，目前弹载捷联惯导系统一般通过传递对准技术提高初始姿态精度。传递对准就是利用载机的火控信息，采用速度匹配、姿态匹配等方法，通过卡尔曼滤波估计并补偿初始姿态误差[1-3]。隐身、超声速的飞行器已经出现在现代战争中，空空导弹的攻击目标存在强烈的时敏性，客观上要求空空导弹面对攻击目标时能够立即发射，从而实现空空导弹的零秒反应，最大限度地避免贻误战机，而传递对准技术存在对准时间和对准精度之间的矛盾，难以满足空空导弹对武器系统快速性的要求。

目前，随着我国自主研发的北斗卫星导航系统的逐步成熟，新型空空导弹已经装备北斗卫星接收机，利用北斗卫星接收机提供的导航信息对弹载捷联惯导系统进行飞行中对准[4-5]成为可能。这种情况下，载机只需要对空空导弹捷联惯导系统进行简单快速的初始化，捷联惯导系统的对准过程在空空导弹飞行过程中进行，可以解决对准时间和对准精度之间的矛盾。同时，由于脱离了载机平台，飞行中对准也能够避免传递对准时载机振动、机翼变形等干扰的影响，与空空导弹传递对准互为备份，提高弹载捷联惯导系统初始对准的可靠性。

本文以北斗卫星导航信息辅助下的弹载捷联惯导系统飞行中对准算法为研究对象，设计惯性系下基于北斗卫星伪距/伪距率的飞行中对准模型，并通过数学仿真试验验证该算法的有效性。

1 飞行中对准模型建立

1.1 飞行中对准系统状态方程

导航坐标系(n系)选择发射惯性系，其原点位于导弹准备时刻载机下方的海平面上，导弹发射点处的北天东地理坐标系，该坐标系的坐标轴向保持惯性空间不变，弹体坐标系(b系)为常规的前上右坐标系。

惯性系下SINS的理想速度如式(1)所示

(1)

根据叠加性误差模型，并忽略重力误差的影响与高阶小量，可以得到速度误差方程如式(2)所示

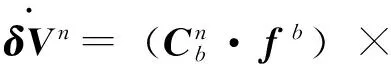
(2)

式中，δVn为惯性系下速度误差，φn为失准角，δfb为载体系下加速度计输出误差。

惯性系下SINS的位置误差δRn只和速度误差δVn有关，如式(3)所示

(3)

姿态四元数Q满足式(4)所示的微分方程

(4)

根据叠加性误差模型，并忽略高阶小量，可以得到失准角方程如式(5)所示

(5)

综上，并考虑陀螺输出常值误差εb和加速度计输出常值误差▽b，飞行中对准系统状态选择X=[δRnδVnφnεb▽b]T，系统状态方程如式(6)所示

(6)

1.2 飞行中对准系统量测方程

北斗卫星接收机测量的第j颗卫星伪距如式(7)所示

(7)

式中，ρj为理想距离，δtu为等效时钟误差相应的距离，vρj为伪距测量噪声。

(8)

将式(8)泰勒级数展开，忽略高阶项，并与式(7)作差，则第j颗卫星的伪距误差如式(9)所示

(9)

为了消除卫星等效时钟误差影响，以仰角最大的那颗卫星(记作第1颗卫星)为基准，分别与其他卫星的伪距误差再次作差，构建第k颗卫星的伪距量测方程

Zρk=[zρk1zρk2zρk3]δRn+vρk

(10)

式中：zρk1=ejx-e1xzρk2=ejy-e1yzρk3=ejz-e1z(k=2，…，j-1)。

同理可得第k颗卫星的伪距率量测方程

(11)

式中，

联立式(10)与式(11)，构建单颗卫星基于伪距/伪距率飞行中对准的观测方程，应用序贯滤波方法即可处理全部接收到的卫星信息。

2 仿真验证

通过数学仿真验证惯性系下，基于北斗卫星伪距/伪距率信息的飞行中对准算法的有效性，飞行中对准的滤波算法采用序贯卡尔曼滤波算法。

2.1 仿真条件

仿真条件设置如下：

1)弹载捷联惯导系统误差设置：陀螺常值漂移为3(°)/h，刻度因数误差3×10-4，加速度计常值偏置1.0mg，刻度因数误差5×10-4。

2)弹载北斗卫星导航信息输出误差设置：伪距误差10m(1σ)，伪距率误差0.5m/s(1σ)，数据更新率10Hz。

3)初始姿态设置：方位0°，俯仰0°，横滚-45°。

4)初始姿态误差设置：方位误差1°，俯仰误差1°，横滚误差1°。

5)初始位置设置：东经120°，北纬40°，高度15km。

6)初始速度设置：600m/s。

7)飞行轨迹采用典型高抛远程弹道，仿真时间300s，滤波周期为0.1s。

2.2 仿真结果

捷联惯导系统的失准角估计误差曲线如图1～图3所示，根据误差曲线可知，飞行中对准算法能够在10s内收敛失准角，有效估计捷联惯导系统的姿态误差，统计10s的失准角误差如表1所示。

图1 x向失准角估计误差曲线Fig.1 Estimation error curve of misalignment angle φx

图2 y向失准角估计误差曲线Fig.2 Estimation error curve of misalignment angle φy

图3 z向失准角估计误差曲线Fig.3 Estimation error curve of misalignment angle φz

x向y向z向失准角误差/(')3.65.41.2

在实际空战环境中，空空导弹必然面临电磁干扰等复杂环境，空空导弹距离攻击目标越近，受到的干扰越强，那么弹载北斗卫星接收机受到干扰的概率也越大。特别是在中制导的后半段，北斗导航系统可能难以正常工作，此时只能依赖惯性导航，其导航误差因惯性传感器随机启动误差的制约而逐步发散。随着空空导弹射程越来越远，中制导段的飞行时间也相应增长，在中制导前半段对惯性传感器随机启动误差进行在线标定将成为可能。在线标定能够提高惯导系统的精度，抑制导航误差发散的程度，保证中制导精度。下面通过x向陀螺常值漂移的估计说明惯性传感器随机误差的在线标定问题。x向陀螺常值漂移估计如图4所示。根据估计曲线可知，飞行中对准算法能够估计惯性传感器的随机误差，惯性传感器随机误差的估计相对失准角而言时间较长。x向陀螺常值漂移估计的快速性和精度统计如表2所示，估计精度用对陀螺常值漂移估计的百分比表示。

图4 x向陀螺常值漂移估计曲线Fig.4 Estimation curve of gyroscope constant drift εx

估计时间/s100150200估计精度/%456780

3 结论

针对空空导弹捷联惯导系统飞行中对准问题，利用弹载北斗卫星导航信息，建立了基于伪距/伪距率的飞行中对准模型，并对北斗卫星接收机钟差、钟漂进行了降维处理。仿真结果表明，在飞行过程中该算法10s内的对准精度优于6′，可以解决传递对准的对准精度和对准时间之间的矛盾，满足空空导弹武器系统快速性的要求。同时，该算法在中制导前半段对惯性传感器随机启动误差进行在线标定补偿，保证中制导精度，提高实际空战中空空导弹的抗干扰能力。

[1] 唐庾梅，鲁浩.空空导弹惯导系统对准的原理与方法[J].航空兵器，1998，(1)：4-7.

[2] 鲁浩，位晓峰，徐剑芸，等.弹载捷联惯导空中传递对准中火控匹配信息精度研究[J].弹箭与制导学报，2011，31(5)：61-64.

[3] 曲法义，魏纪林，崔乃刚，郝淑梅.机载精确制导武器快速传递对准[J].哈尔滨工业大学学报，2014，46(1)：7-10.

[4] 王得朝，康鹏.基于Kalman滤波的飞行中对准技术研究[J].现代防御技术，2009，37(6)：22-25.

[5] 吉庆昌，孔星炜.大航向角误差情况下飞行中对准研究[J].航空电子技术，2012，43(1)：15-19.

[6] 郑辛，符梦印.SINS/GPS紧耦合组合导航[J].中国惯性技术学报，2011，(1)：33-37.

In-flight Alignment for Air-to-air Missile

ZHOU Ben-chuan，LU Hao，DUAN Chao-yang

(Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons，China Airborne Missile Academy，Luoyang 471099，China)

In order to solve the contradiction between precision and rapidity in SINS transfer alignment for air-to-air missile，a new in-flight alignment algorithm is proposed in this paper，according to the missile-borne BDS navigation information.The in-flight alignment model based on pseudo range/pseudo range rate in inertial frame is derived in detail，the model reduction of clock error and clock frequency drift of Beidou receiver is proposed，the measurement equation of in-flight alignment model is optimized.Simulation results show that the algorithm can realize SINS initial alignment during the flight，the alignment precision is better than 6 arc minutes in 10 second，and the algorithm can calibrate the random error of the inertial sensor online，it can increase navigation accuracy of missile-borne SINS and anti-jamming of air-to-air missile further.

In-flight alignment；Pseudo-range/pseudo-range rate；Online calibration

2015-11-05；

2015-11-30。

周本川(1984-)，男，高级工程师，主要从事捷联惯性导航和卫星组合导航技术与应用方面的研究。

U666.1

A

2095-8110(2016)01-0009-04