星敏与磁强计安装矩阵的户外标定

孙 闯,王凯强,任顺清

(哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001)

星敏与磁强计安装矩阵的户外标定

孙 闯,王凯强,任顺清

(哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001)

为了提高卫星测量地磁场参数的精度，必须提高卫星上星敏与磁强计安装矩阵的测量精度，因此，提供了一种借助地磁场与地面观星对星敏与磁强计安装矩阵进行户外地面标定的方法。首先建立了三轴磁强计的误差模型，利用磁强计在地磁场中进行翻滚试验标定了误差模型系数，同时给出了3个敏感轴矢量在地理坐标系下的表示。其次利用星敏观星，测量了星敏光轴单位矢量相对地理坐标系的表示。最后以地理坐标系为桥梁，给出了星敏与磁强计之间的安装矩阵。对该方法进行了仿真，结果表明其能有效准确地辨识出磁强计误差模型中的各项误差系数以及星敏与磁强计安装矩阵。

星敏;三轴磁强计；安装矩阵;标定;误差模型

0 引言

在卫星地磁测量中，通过磁强计测量的数据得到磁场强度矢量在地理坐标系上的精确投影，为航天、航空、航海等设备提供导航参数。地磁的测量受到传感器本身和非理想安装等因素的影响，其坐标系间的转换也对磁测精度产生影响。因此，保证卫星磁测设备本身的测量精度和星敏感器与磁强计之间安装矩阵的测量精度具有非常重要的意义[1-5]。

关于星敏与三轴磁强计的地面标定可在实验室环境下进行。利用标准磁场对磁强计进行标定与补偿[5]，通常通过迭代、最小二乘与卡尔曼滤波等方法对误差模型进行辨识[6-8]。利用星仿真器对星敏进行标定，可以达到较高精度且试验周期短[9-10]。实验室标定虽然能够达到较高的标定精度，但对实验设备要求较高。为了克服其局限性，降低标定成本，有学者提出室外天顶星敏标定方法[11]，文献[12]和文献[13]也采用了新的标定实验平台与标定步骤来简化实验条件和计算难度。

不论室内还是室外标定，目前人们主要研究方向都是分别对星敏和磁强计进行标定，对星敏与磁强计安装矩阵进行标定的研究较少。本文提出一种星敏与磁强计安装矩阵的户外标定方法，不仅可借助已知地磁场强度对三轴磁强计的误差进行标定，克服传统标定方法复杂和环境苛刻的问题[14]，还可根据星敏感器与磁强计敏感轴坐标系相对地理坐标系的姿态辨识出星敏与三轴磁强计间的安装矩阵。

1 户外标定系统的简要介绍

展杆与夹具连接在一起，放置在水平的平板上。夹具体与标准六面体紧密靠在一起。建立相应的坐标系包括：

1)地心惯性坐标系OXIYIZI，以地球的球心O为原点，OXI轴沿赤道平面与黄道面的交线，OZI轴沿地轴指向地球的北极，OYI轴在赤道平面内与OXI轴和OZI轴构成右手坐标系。

2)地理坐标系OX1Y1Z1，OX1水平向东，OZ1指向天顶且与重力加速度矢量平行，OY1水平指北。在得知某点经纬度，格林威治恒星时t，当地经度λ、纬度L后，地理坐标系相对于惯性空间的姿态为

(1)

3)标准六面体坐标系OX2Y2Z2，OZ2轴与标准六面体的表面呈90°关系，OX2轴与地理坐标系OX1轴存在方位角，记为φ，OY2轴与OX2、OZ2轴呈90°关系。

4)磁强计测量坐标系OX3Y3Z3，OZ3轴与标准六面体坐标系的OZ2轴一致，初始位置OX3轴与OX2轴重合，OY3轴与OX3、OZ3轴呈90°关系。

5)星敏基准轴坐标系OXpYpZp，设OpXp与X星敏的基准平行，OpYp与Y星敏的基准平行，OpZp与Z星敏的基准平行。

户外标定中，在地磁场已知的情况下，初始调整磁强计OX3与OX2平行，OY3轴与OX3呈90°关系，OZ3竖直向上。通过分别靠在标准六面体立的四面，就可以得到磁强计3个敏感轴在不同角度下的输出磁场强度。

2 三轴磁强计误差源及其安装误差

由于加工水平与安装工艺的限制，以及磁强计的内部存在剩磁，磁强计本身的主要误差包括标度因子误差kx、ky、kz和零偏误差BX0、BY0、BZ0。

分析户外标定系统可知其主要安装误差包括平板水平度误差、定位块方位角误差和磁强计三敏感轴非正交误差，相邻坐标系之间的齐次变换式如下：

1)在标定过程中不能确保夹具体与标准六面体完全契合，设存在小角度误差Δφ，称为方位角误差。标准六面体坐标系相对地理坐标系的姿态矩阵为

(2)

2)在标定过程中，夹具体绕标准六面体4个侧面旋转。即可认为它是在标准六面体坐标系的基础上，绕OZ3轴旋转γ角度(γ=0,90°,180°,270°)，磁强计测量坐标系相对六面体坐标系的姿态矩阵为

(3)

3)磁强计3个敏感轴存在非正交误差Δθyx、Δθxy、Δθzx、Δθxz、Δθyz、Δθyz。磁强计三轴坐标系的单位向量在磁强计测量坐标系OX3Y3Z3的表示为

(4)

3 三轴磁强计误差模型

由式(1)～式(4)，计算出三轴磁强计坐标系相对于地理坐标系的齐次变换矩阵为

(5)

结合给定的三轴磁强计刻度因子误差与零偏误差，磁强计的3个敏感轴的误差模型为

(6)

式中，RX、RY、RZ为磁强计输出值，单位为nT；BX，BY，BZ为实际地磁强度，单位为nT；ε为残余误差，单位为nT。

4 磁强计户外标定方法

整个标定过程大体分为三个步骤：

(7)

(8)

(9)

根据磁强计的户外标定，可知在格林威治恒星时ti时刻，测量的磁强计的敏感轴矢量初始位置在地理坐标系下表示为

(10)

(11)

(12)

式中，j=1,2,3。以磁强计的输出RX为例，将磁强计坐标系相对于地理坐标系的姿态变换矩阵代入到磁强计的误差模型中，忽略二阶无穷小量，计算在标定的三个步骤中的输出。由式(1)～式(7)可知，磁强计RX在第一步的输出为

kxΔθxzBZ+ε

(13)

整理得到

RX1i=a1,1ix1+a2,1ix2+a3,1ix3+a4,1ix4+x5+ε

(14)

(15)

[x1x2x3x4x5]T=

[kxkxΔθxykxΔφkxΔθxzBX0]T

(16)

采用相同方法，可得到在标定的第二步与第三步计算磁强计的输出RX2i和RX3i。

最终整理，化成矩阵的形式为

(17)

式(17)的矩阵表达式可简写为

RX=ΦxX+ε

(18)

基于最小二乘原理，对式(18)中的kx、kxΔφ、kxΔθxy、kxΔθxz、BX0进行参数辨识

(19)

同理，可推导出磁强计另外两个敏感轴误差项参数辨识的表达式分别为：

(20)

(21)

对式(20)、式(21)中的参数进行辨识，即可分别辨识出参数ky、kz、Δφ、Δθyx、Δθzx、Δθzy、Δθyz、BY0、BZ0。对于重复辨识出的Δφ，可采用取平均的方法减小误差。将辨识得到的相关参数代入式(10)～式(12)中，就能得到磁强计的三个敏感轴矢量初始位置在地理坐标系下的表示。

5 星敏与磁强计安装矩阵户外标定方法

在12个位置测量磁强计的同时，记录每一个星敏感器的基准矢量和格林威治恒星时ti。设星敏感器观测到的星体赤经为αi和赤纬为δi，则该星体的单位星矢在惯性坐标系下的表示为[15]

Ai=[cosαicosδisinαicosδisinδi]T

(22)

设星敏感器图像中星象中心坐标为(xi,yi)，f为光学系统焦距。恒星单位矢量在星敏坐标系中表示为

(23)

以某个时刻与位置测量X星敏的输出为例，当X星敏观测到n(n≥3)颗恒星时，有

(24)

写成矩阵的形式

(25)

根据最小二乘法得到

(26)

(27)

结合式(1)，得到此向量在地理坐标系下的表示为

(28)

(29)

6 算例验证

为了验证本文提出误差模型与标定方法的正确性，基于上述分析与推导结果进行算例验证。设定实际地磁强度为：BX=25000nT，BY=28000nT，BZ=32000nT。假设三轴磁强计中的方位角φ=0，随机误差为10nT。磁强计的各个误差项的设定如表1所示，通过误差模型可计算出磁强计的各个模拟测量值，根据式(18)～式(21)对各误差模型系数进行计算，辨识结果如表1所示。分析表1的辨识结果，本方法在对磁强计刻度因子误差的辨识上有着较高的精度，三个参数的相对误差均低于1%，在对小角度的方位角误差上也取得了较高的辨识精度。而对于磁强计的零偏误差辨识，相对误差较大，分析原因主要是零偏误差设定与随机误差相近，并且地磁场设定值较大，因此相对误差较大，但其绝对误差结果均不超过5nT。

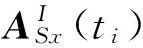
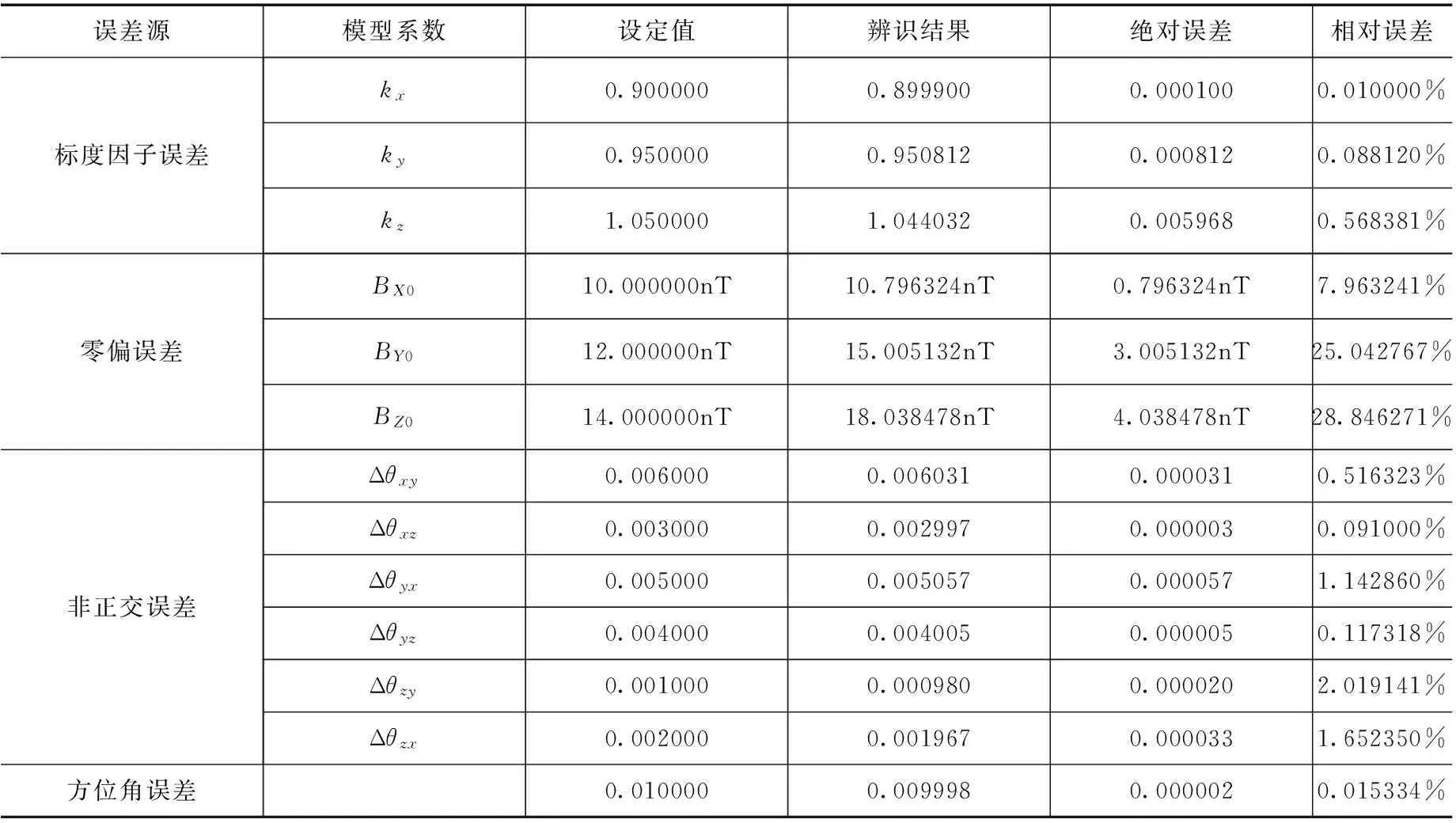
表1 磁强计误差模型系数辨识结果Tab.1 Magnetometer error model coefficients identification results

表2 安装矩阵系数辨识结果Tab.2 Installation matrix coefficients identification results

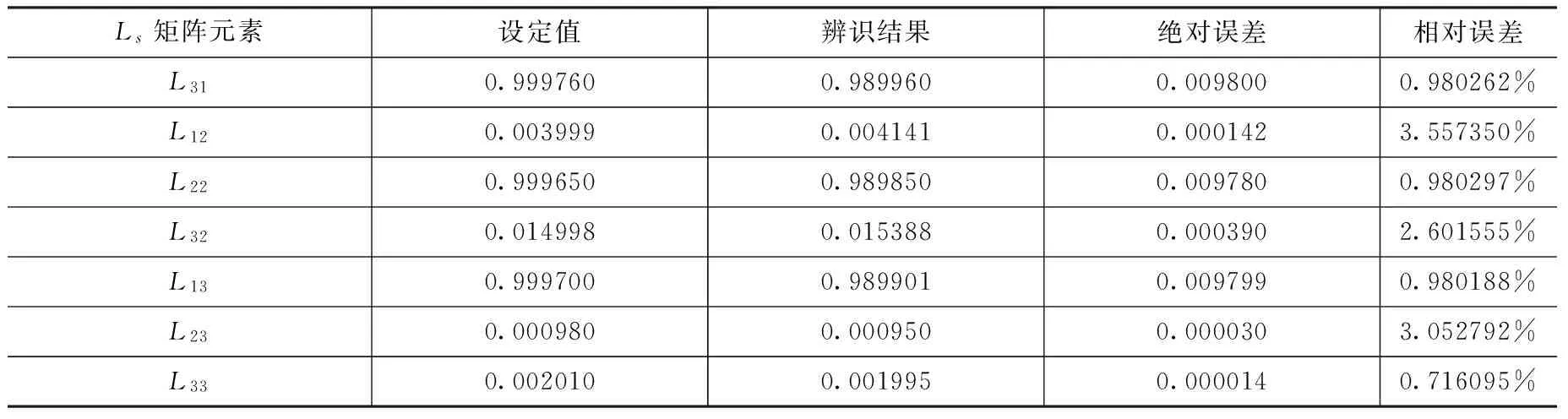
续表

由表2可知，本方法能够对星敏与磁强计的安装矩阵进行精确的参数辨识，大部分辨识相对误差均低于1%。其中几项的辨识误差相对较大，分析原因主要有两点：首先，设定数值较小，增加了辨识的难度与计算误差；其次，由于算法验证采用的是最低要求的3颗星进行辨识，因此对于安装矩阵参数的辨识精度有所限制，当星敏采集星数超过3颗时，会提高辨识精度，减小相应误差。

7 结论

本文设计了借助地磁场在户外标定星敏与磁强计安装矩阵的方法。该方法标定了磁强计相对于当地地理坐标系的安装矩阵和磁强计的误差模型系数，抑制了磁强计误差模型系数变化对安装矩阵标定的影响。在夜晚能见度较好时，可以标定星敏对于地理坐标系的安装矩阵。通过地理坐标系转换，可以标定出星敏与磁强计之间安装矩阵。通过算例分析，验证了该方法能够达到较高的标定精度。

[1] Fei X,Ying D,Zheng Y.Laboratory calibration of star tracker with brightness independent star identification strategy[J]. Optical Engineering,2006，45(6):43-48.

[2] Habib T M A.Fast converging with high accuracy estimates of satellite attitude and orbit based on magnetometer augmented with gyro,star sensor and GPS via extended Kalman filter[J].The Egyptian Journal of Remote Sensing and Space Sciences,2011,14(2):57-61.

[3] 杨照华,余远金,祁振强.空间环境探测卫星用磁强计误差分析及在线标定[J].宇航学报,2012,33(8):1104-1111.

[4] Simpson D G,Vinas A F.NASA computational case study：modeling planetary magnetic and gravitational fields[J]. Computing in Science & Engineering,2014,16(4):73-79.

[5] 郝东,绳涛,陈小前.三轴磁强计测量误差修正方法[J].航天器环境工程,2011,28(05):463-466.

[6] 刘艳霞,李希胜,窦晓霞.基于椭球假设的三轴磁强计标定算法改进[J].计算机测量与控制,2013,21(6):1590-1593.

[7] Vasconcelos J F,Elkaim G,Silvestre C,Oliveira P,Cardeira B.Geometric approach to strapdown magnetometer calibration in sensor frame[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2)：1293-1306.

[8] Beravs T,Begus S,Podobnik,J,Munih M.Magnetometer calibration using Kalman filter covariance matrix for online estimation of magnetic field orientation[J].IEEE Transactions on Instrumentation and Measurement,2014,63(8)：2013-2020.

[9] 贺鹏举,梁斌,张涛,杨君.大视场星敏感器标定技术研究[J].光学学报,2011,31(10):200-206.

[10] Li Y T,Zhang J,H W W,Tian J W.Laboratory calibration of star sensor with installation error using a nonlinear distortion model[J].Applied Physics B,2014,115(4)：561-570.

[11] 李春艳,李怀锋,孙才红.高精度星敏感器天文标定方法及观测分析[J].光学精密工程,2006,14(4):558-563.

[12] Zikmund A,Janosek M,Ulvr M,Kupec J.Precise calibration method for triaxial magnetometers not requiring earth’s field compensation[J].IEEE Transactions on Instrumentation and Measurement，2015,64(5):1250-1255.

[13] Ghanbarpour A H,Pourtakdoust S H,Samani M.A new non-linear algorithm for complete pre-flight calibration of magnetometers in the geomagnetic field domain[J].Journal of Aerospace Engineering,2009,223(6)：729-739.

[14] Song Z G,Zhang J S,Zhang X H,Xi X L.A calibration method of three-axis magnetometer with noise suppression[J]. IEEE Transactions on Magnetics,2014,50(11)：1-4.

[15] 钟红军,杨孟飞,卢欣.星敏感器标定方法研究[J].光学学报,2010,30(5):1343-1348.

Calibration of Installing Matrix Between Magnetometer and Star Sensor

SUN Chuang,WANG Kai-qiang,REN Shun-qing

(Space Control and Inertial Technology Research Center,Harbin Institute of Technology,Harbin 150001,China)

In order to enhance the measurement accuracy of the parameters of the geomagnetic field,the installing matrix between three star sensors and three-axis magnetometer must be precisely measured.The method of measuring the matrix was put forward by way of the geomagnetic field and observing the stars in outdoor open field.The error model about the three-axis magnetometer was established at first,through tumble test in the geomagnetic field,the coefficients of the error model was calibrated and the representations of three unit vectors of magnetometer’s sensitive axes in the geography coordinate system were achieved.3 unit vectors’ denotations of star sensors in the geography coordinate system were also gained by observing stars.Using geography coordinate system as a bridge,the installing matrix between star sensors and magnetometer was attained.It is proved that the installing matrix is identified effectively and precisely by simulation calculation.

Star sensor；Three-axis magnetometer；Installing matrix；Calibration；Error model

2015-11-19；

2016-01-04。

孙闯(1989-)，男，博士，主要从事惯性技术与测试方面研究。E-mail：sun489495923@163.com

TH762

A

2095-8110(2016)02-0077-06