一种基于相对测量信息的SINS/USBL组合导航算法

张亚文，莫明岗，马小艳，邓继权

(北京自动化控制设备研究所，北京 100074)

一种基于相对测量信息的SINS/USBL组合导航算法

张亚文，莫明岗，马小艳，邓继权

(北京自动化控制设备研究所，北京 100074)

针对使用传统位置匹配算法解决SINS/USBL组合导航的问题，需要先利用USBL输出信息实时求解出载体的绝对位置，设计了一种基于相对测量信息的SINS/USBL组合导航算法。该算法无需求解绝对位置，直接利用超短基线系统原始输出的高度角、方位角和斜距等相对测量信息进行卡尔曼滤波组合导航，且在滤波器设计时能够根据传感器测量精度对滤波参数进行设计，更有针对性。通过理论数据仿真和湖面试验数据处理，证明了该组合导航算法能够在一定程度上提高导航精度，具有可行性。

组合导航；相对测量信息；直接输出

0 引言

捷联惯导系统(SINS)能够在较短的时间内为水中载体提供精确的位置信息，但随着时间推移，误差累积会严重影响导航精度，需要额外的信息对该误差进行修正[1]。超短基线(USBL)定位系统能够测量应答器相对于基阵的高精度位置信息[2-3]，可以用来抑制惯导系统误差的发散。此外，超短基线定位系统以其成本低、便携性强、灵活性高和操作简单等特点，在海洋工程、海洋矿产资源、水下考古、海洋国防建设等领域中得到了广泛应用[4]。因此，SINS/USBL组合导航成为了水下导航技术研究的热点。

传统的SINS/USBL组合导航方法，主要是参考通用位置匹配算法，即以惯性导航系统给出的经度、纬度和高度与辅助导航定位设备给出的相应信息的差值作为位置观测量。然而，由于USBL直接输出的是应答器相对于基阵的距离和方位信息，即高度角α、方位角β和斜距R[5]。若利用传统位置匹配算法，则需要先利用USBL输出的相对距离和方位、应答器的绝对位置、姿态矩阵和USBL与姿态传感器之间的标定矩阵等信息，求解出载体的绝对位置信息(经纬高)，然后才能进行组合导航。由于受到标定误差、姿态误差等影响，直接解算的位置存在一定的误差，会影响精度。此外，在滤波器设计时，无法根据USBL传感器精度，合理选取部分滤波参数。针对以上问题，结合USBL自身输出特点，提出并设计一种直接利用USBL输出的高度角、方位角和斜距等相对测量信息的SINS/USBL组合导航算法。在模型中考虑姿态误差和安装误差等因素，能够在一定程度上提高定位精度。

1 超短基线定位方式及定位误差分析

超短基线定位系统主要由水声收发基阵和应答器构成。通过测量声波传回基阵各基元之间的相位差，实现对应答器的测向，获得应答器相对于基阵的高度角α和方位角β；通过测量接收时刻和发射时刻的时间延迟，实现对应答器的测距，获得应答器相对于基阵的斜距R[6]。最终利用高度角α和方位角β将斜距R投影到基阵坐标系中，可得基阵坐标系中应答器相对于基阵中心的位置信息(x，y，z)

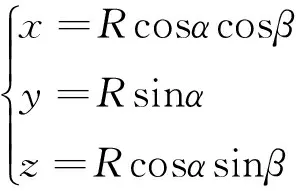
(1)

这便是USBL相对定位的基本原理。USBL绝对定位工作原理如图1所示。

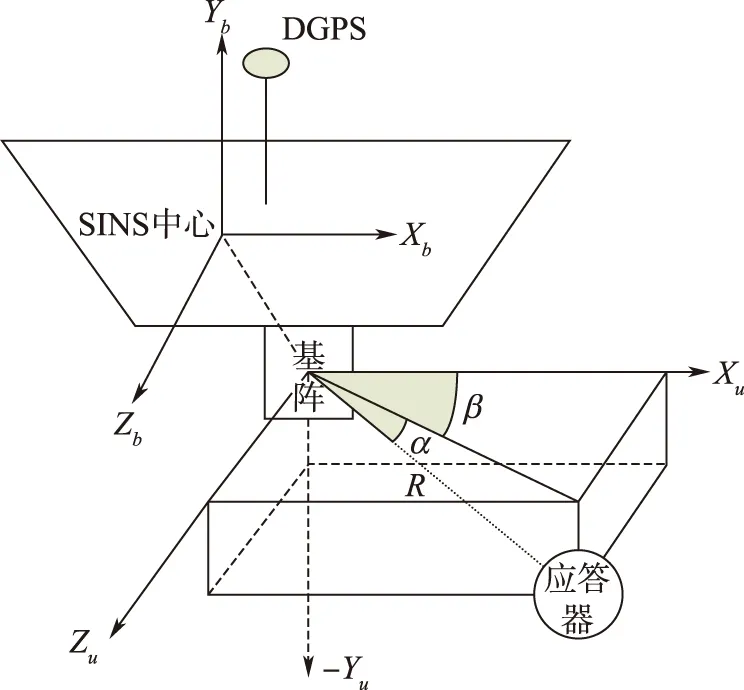
图1 USBL定位原理图Fig.1 The scheme of USBL positioning theory

(2)

超短基线系统的定位误差源可分为以下两类：

1)传感器误差：USBL基阵测距误差、USBL测角误差、测距交会求解造成的误差、超短基线基阵阵元相位差引起的误差、声传播引起的误差、声学噪声引起的误差等，此类误差大都受制于超短基线设备本身的性能指标。

2)系统误差：此类误差常存在于使用过程中，包括：外部航向姿态误差、基阵坐标系和姿态传感器坐标系之间的安装角误差和应答器的绝对位置误差等。后两种误差源常通过事先高精度的标定校准来减小。

本文提出并设计的SINS/USBL组合导航算法在惯导误差建模的基础上，将对测距误差、测角误差和两坐标系间的安装角误差等三项误差源进行建模补偿。

2 组合导航模型及滤波方程

2.1 组合导航系统状态模型

组合导航系统误差状态模型包括SINS的误差状态模型和USBL的误差状态模型。

2.1.1SINS的误差状态模型

(3)

捷联惯性导航误差状态方程为

(4)

2.1.2USBL的误差状态模型

通过实验数据处理发现，USBL自身测角精度以及USBL基阵坐标系到SINS载体坐标系的安装角标定精度对定位精度影响很大。从数值角度粗略分析：如果USBL测量的方位角β或者航向安装误差角θy有1°误差，则会引入约1.7%R的水平位置误差，而且随着斜距R变大误差会进一步增大。USBL的测角精度和噪声受USBL设备的限制，但测角误差在工作范围内都为小角度。此外，安装角误差可以通过事先标定使其减小为一个小角度误差，因此，本文将USBL到SINS的安装误差角θ=[θxθyθz]T和高度角α和方位角β的误差[δαδβ]设计为卡尔曼滤波组合导航的误差状态量。

由于海洋环境并不安静，波浪、船只和波浪所形成的空气气泡及温度、盐度等水文气象要素都对超短基线水声定位系统起着不可忽视的作用[8]，主要影响声波的传播，即对USBL的测距精度产生影响。故也将USBL测距精度误差δKd设计为卡尔曼滤波组合导航的误差状态量。

综上所述，USBL的误差状态量为

XUSBL=[θxθyθzδαδβδKd]T

(5)

由于安装误差角、测角误差和USBL测距精度误差等均为小量，因此视为随机常数。对应的卡尔曼滤波状态方程为

(6)

其中：FUSBL=[06×6]。

2.1.3 组合导航系统误差状态模型

结合2.1.1和2.1.2可得，21维的组合导航系统误差状态量为

X=[XSINSXUSBL]T

(7)

则组合导航系统误差状态方程为

(8)

简化误差状态方程为

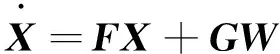
(9)

2.2 组合导航系统观测模型

基阵坐标系中应答器相对于惯导的高度角、方位角和斜距为

(10)

对其求偏微分可得

(11)

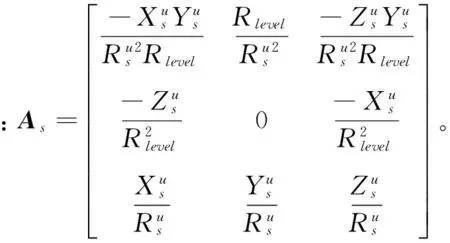
为了求得更加精准的位置信息，避免球面坐标系中小角度近似误差，因此本文选取在模型更加精准的地球直角坐标系中进行位置求解。地球直角坐标系的原点o位于旋转椭球体中心，z轴与地球自转轴重合，正向沿地球自转方向，x轴和y轴位于赤道平面内，x轴穿过本初子午线，y轴穿过东经90°子午线。

应答器的位置为Pr=[φrhrλr]，惯导解算的位置为Ps=[φshsλs]，通过地球定位中球面坐标系到直角坐标系的转换公式[9]，则二者在地球直角坐标系的相对位置为re

(12)

通过坐标变化并补偿杆臂误差，得到基阵坐标系u中应答器相对惯导的位置

(13)

引入误差量可得

(14)

则有

(15)

综合式(10)～式(15)可得

(16)

其中：

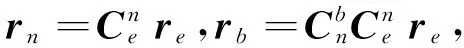
令高度角、方位角和斜距的真值依次为α、β、R，则有

(17)

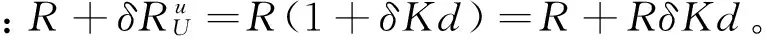
故观测方程为

(18)

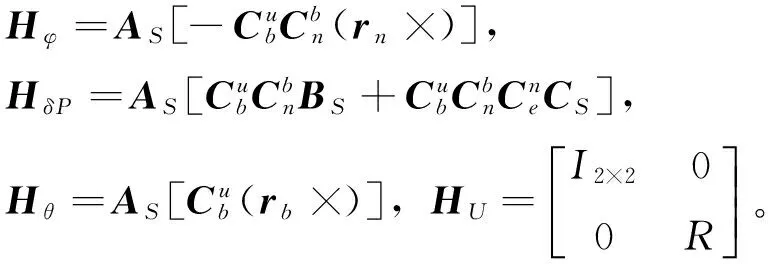
则观测矩阵为

H=[ 03×3(Hφ)3×3(HδP)3×306×3

(Hθ)3×3(HU)3×3]

(19)

简化观测方程为

Z=HX+v

(20)

2.3 卡尔曼滤波模型

对式(9)和式(20)进行离散化处理可得SINS/USBL组合导航的卡尔曼滤波模型为

(21)

其中，Wk和Vk+1均为白噪声，且方差阵依次为Q、R。

本方法采用标准卡尔曼滤波算法基本方程[10]，选择合适的滤波初值(状态初始值、初始估计均方误差阵、系统噪声初始方差阵以及量测噪声方差阵)，进行滤波估计，并实时修正速度、姿态和位置信息。

3 理论数据仿真分析

惯导初始地理位置北纬39.8°东经116.2°高度为0，以3m/s(约6节)的前向速度环绕应答器(北纬39.8000235°东经116.199167°，高度-50m)行驶1000s，理想初始航向姿态角都为0°。惯导采样周期为5ms，USBL数据更新周期为2s，组合导航周期为2s。各传感器误差源和初始误差设置如表1所示。

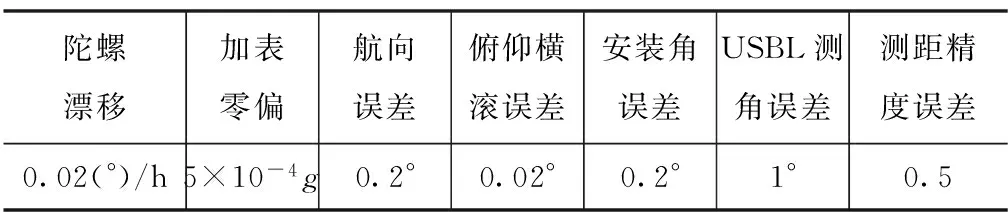
表1 传感器误差源和导航初始误差设置Tab.1 Error of the sensor and initial navigation

按照本文设计的基于相对测量信息组合导航算法进行仿真，并与纯惯性导航和USBL定位进行对比，如表2所示，本方法1σ定位精度2倍优于USBL定位。误差曲线如图2～图7。

表2 1σ定位精度对比Tab.2 The comparison of positioning precision

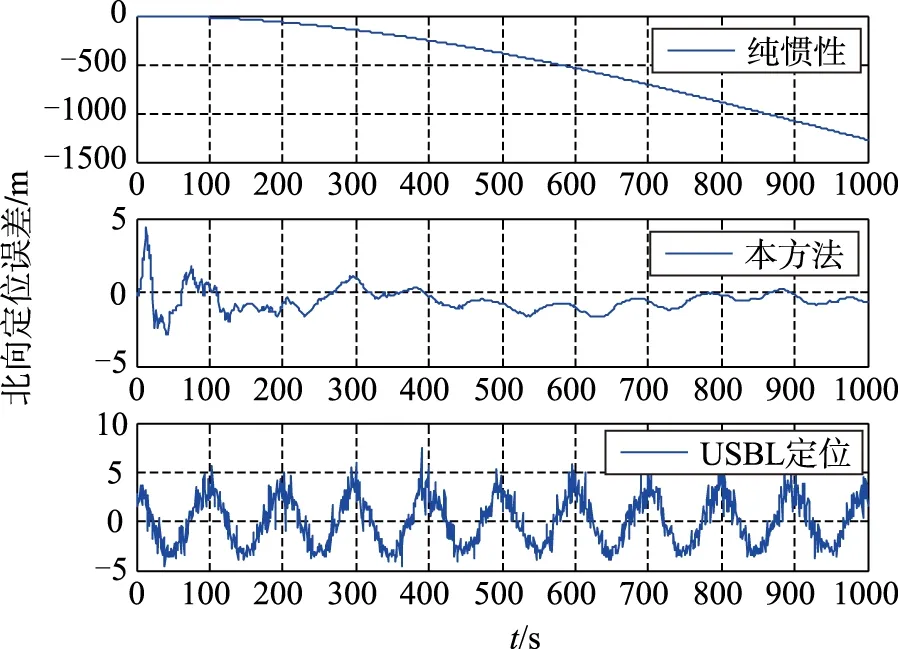
图2 北向位置误差图Fig.2 North position error

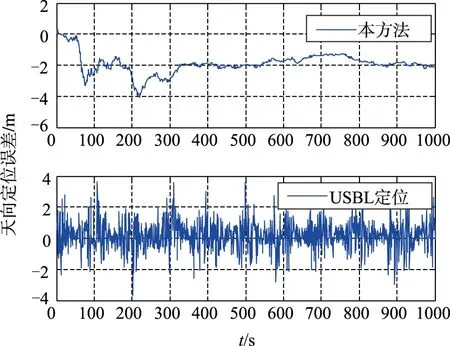
图3 天向位置误差Fig.3 Up position error

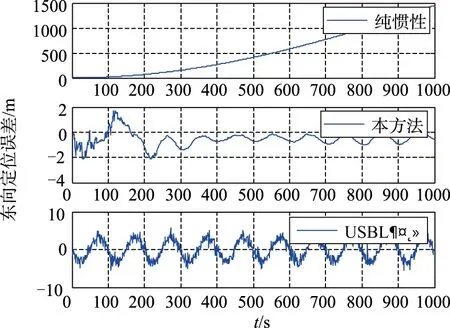
图4 东向位置误差Fig.4 East position error

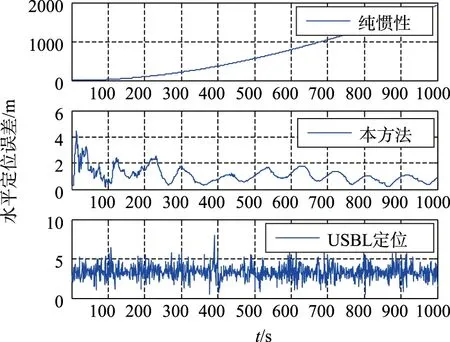
图5 水平定位误差Fig.5 Horizontal position error

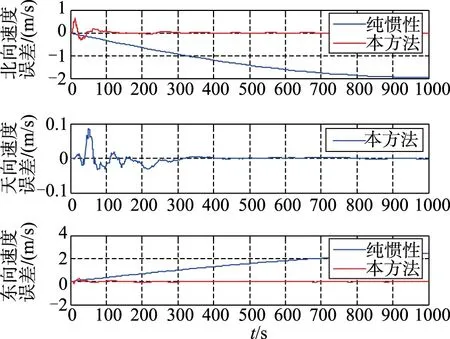
图6 北天东速度误差Fig.6 The comparison of velocity error

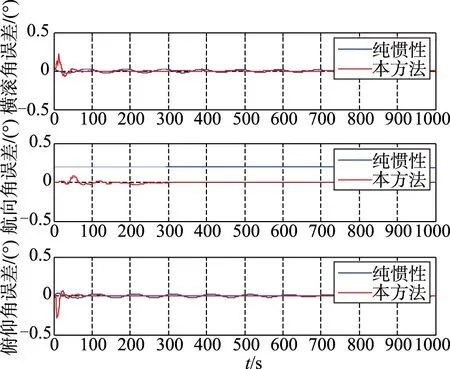
图7 横滚角、航向角、俯仰角误差Fig.7 The comparison of attitude error

从图2～图5定位误差曲线可以看出，本算法能够有效地抑制位置误差发散，且位置误差不随时间增长；图6速度误差曲线显示出本方法能够有效地抑制速度误差发散；从图7航向姿态误差曲线可以看出，本方法能够比较有效地抑制航向角误差和水平姿态角误差。综上所述，在理论仿真情况下，本文设计的基于相对测量信息的SINS/USBL水下组合导航算法，不仅能有效地抑制速度误差和位置误差，还能够估计惯导的航向姿态误差，验证了理论仿真情况下的本算法的可行性。

4 湖面实验数据处理分析

湖面试验系统主要包括：光纤捷联惯导系统(SINS)、USBL系统和DGPS系统。光纤陀螺漂移优于0.02(°)/h，加表零偏优于30μg(1σ)。USBL系统采用NavQuest公司的Track Link 1500HA水下基阵和应答器，其原始输出为高度角、方位角和斜距，其测角精度优于1°，定位精度为0.5%，数据更新周期为2s。

利用本文设计的基于相对测量信息的SINS/USBL组合导航算法对湖面试验采集的一组约为5 000s导航原始数据进行处理分析，并以DGPS的位置为基准信息，考核组合导航算法的定位精度，并与传统位置匹配算法进行对比。组合导航初始时刻，先用DGPS对惯导的解算的位置速度进行重置，以避免原始积累的误差对组合导航精度考核产生影响[11]。

从表3湖面试验定位精度可以看出，本方法定位精度(1σ)相比传统位置匹配算法有一定的提高。从图8～图10湖面试验定位误差曲线可以看出，相比传统算法，本算法不仅能够有效抑制惯导位置的发散，且定位误差更小、更加平滑。结合图11 USBL数据有效性判定结果可以看出，位置误差噪声主要由于USBL数据判定无效，导致组合导航不再进行量测更新，只进行时间更新引起。综上所述，本文设计的基于相对测量信息的SINS/USBL水下组合导航算法能有效地抑制速度误差，且能一定程度上提高组合导航定位精度，即验证了湖面试验数据情况下本算法的可行性。

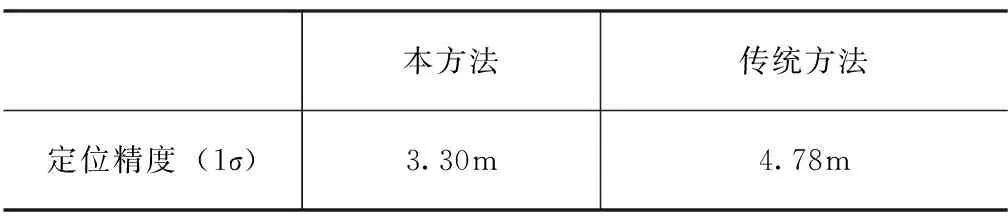
表3 湖面试验定位精度Tab.3 The comparison of lake test position precision

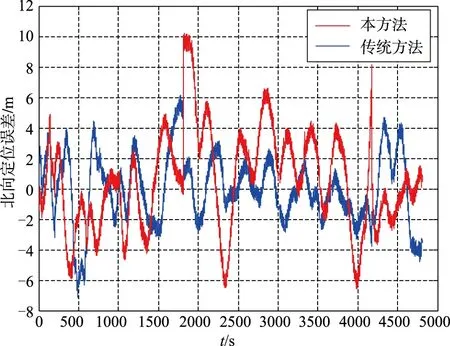
图8 北向位置误差曲线Fig.8 North position error

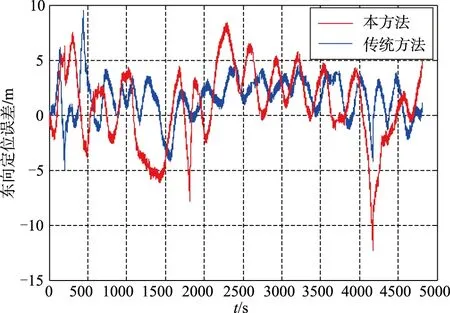
图9 东向位置误差曲线Fig.9 East position error

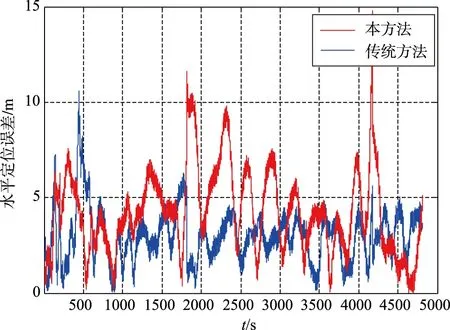
图10 水平定位误差曲线Fig.10 Horizontal position error

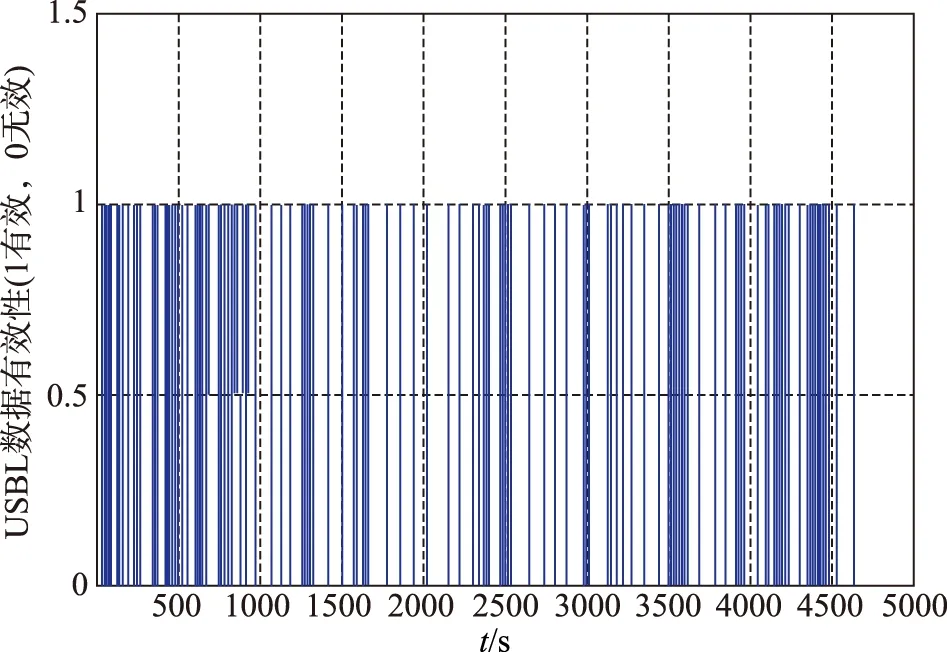
图11 USBL数据有效性判定结果Fig.11 USBL data valid judge result

5 结论

本文设计的基于相对测量信息的SINS/USBL组合导航算法，利用了工程使用中USBL设备实际输出为高度角、方位角和斜距的特点，摒弃了传统算法中绝对位置的解算，且在滤波器设计时能够根据传感器测量精度对量测噪声进行设计，更有针对性地解决了SINS/USBL组合导航的问题。理论仿真和湖面试验数据处理表明，本算法能够实现高精度的水下导航定位，且能够一定程度上提高组合导航定位精度，具有可行性。

[1] 兰华林，孙大军，张殿伦，李想.单应答器导航深海实验[J].海洋工程，2007,25(2)：110-113.

[2] 隋海琛，田春和，韩德忠，王崇明.水下定位系统误差分析[J].水道港口,2010,31(1):69-72.

[3] LinkQuestInc.TrackLink 1500 USBL Tracking System,User’s Guide Version 1500.7.2.

[4] 王德刚，韩富江，来向华，苟诤慷，傅晓明.国家海洋局第二海洋研究所研究报告[J].海洋科学，2011,35(2):77-78.

[5] LinkQuestInc.TrackLink 1500 USBL Tracking System,User’s Guide Version 1500.7.2

[6] 王德刚,韩富江,来向华,苟诤慷,傅晓明.超短基线定位原理及校正方法研究[J].海洋科学,2011,35(2):77-80.

[7] 秦永元.惯性导航[M].北京:科学出版社,2006.

[8] 冯守珍,吴永亭,唐秋华.超短基线声学定位原理及其应用[J].海岸工程,2002,21(4):13-18.

[9] 史海锋,张卫斌.空间直角坐标与大地坐标转换算法研究[J].大地测量与地球动力学,2012,32(5):78-81.

[10] 秦永元,张洪钺,汪淑华.卡尔曼滤波与组合导航原理[M].西安：西北工业大学出版社,1998.

[11] 唐康华,江明明,翁炬.基于自适应滤波的水下SINS/相控阵DVL组合导航算法设计[J].中国惯性技术学报,2013,21(1):66-70.

An Algorithm Used in Underwater SINS/USBL Integrated Navigation

ZHANG Ya-wen，MO Ming-gang，MA Xiao-yan，DENG Ji-quan

(Beijing Institute of Automatic Control Equipment，Beijing 100074，China)

For the problem that the traditional position integrated navigation must be working after the absolute position of the USBL (Ultra Short Base Line) was evaluated，design a new integrated navigation algorithm which observes the relative measurement information.The algorithm no longer needs to evaluate the absolute position，and it can do the KF integrated navigation by means of observing the immediate data of USBL outputs，the relative measurement information(depression，bearing and range )，and design the KF parameter based on the USBL sensor measurement precision.Besides，a theory simulation and a lake test data analysis prove the improvement and the practicability of the new integrated navigation algorithm.

Integrated navigation；Relative measurement information；Immediate output

2014-11-18；

2015-03-02。

张亚文(1990-)，男，硕士，助理工程师，主要从事惯性/水声组合导航技术研究。E-mail:zhangyawen0927@126.com

V249

A

2095-8110(2016)02-0007-07