基于FPGA实现的归一化空时自适应抗干扰技术
2016-03-16付晶晶武成锋何子君
付晶晶,李 峰,武成锋,何子君
(北京自动化控制设备研究所,北京100074)
基于FPGA实现的归一化空时自适应抗干扰技术
付晶晶,李 峰,武成锋,何子君
(北京自动化控制设备研究所,北京100074)
针对压制干扰源提出一种基于FPGA实现的归一化空时自适应抗干扰技术。通过主通道功率统计值调节步长因子,达到归一化处理的目的,当x(n)较大时,可以解决梯度噪声放大的问题,有效地提高了算法的抗干扰能力;不需要计算u(n)的平方欧氏范数,不包含除法运算,减少了计算量,易于FPGA工程实现;通过计算机仿真分析和外场试验验证了该技术有效地提高了算法收敛速度和干扰抑制能力。
归一化;空时自适应;抗干扰
0 引言
随着卫星接收机的普遍应用,卫星信号易受干扰的问题显得越来越突出,抗干扰技术在弹载、机载、舰载等军用领域卫星接收机中逐渐得到广泛应用,大大提高了复杂战场环境中接收机对干扰的抑制能力[1-3]。目前卫星导航抗干扰技术主要有:时域滤波技术、频域滤波技术、空域滤波技术以及空时滤波技术等[4]。单纯的空域滤波技术是建立在窄带假设基础上[5-8],空时自适应抗干扰技术是一种宽带技术[9],在实际应用中,信号多径是宽带的,针对卫星制导恶意干扰大多也是宽带干扰,该技术在卫星信号抗干扰方面的应用是进步性的[10]。空时自适应处理方法尽管能带来好的抗干扰效果,但运算量增加显著。目前主要有空时协方差矩阵求逆和自适应权值迭代两种权值计算方法[11-12]。空时协方差矩阵求逆法最优处理的运算量约为O[(MN)3],随着空时处理维数的增加,运算量成指数倍(立方)增长;自适应权值迭代法随处理器维数的增大,自适应算法的收敛性能和干扰跟踪能力降低,难以应付时变干扰场景。
鉴于上述问题,本文针对压制干扰源提出一种归一化空时自适应抗干扰技术。该技术通过主通道功率统计值自适应调节步长因子,进行归一化处理,达到降低梯度噪声、提高收敛速度的目的;且不需要计算u(n)的平方欧氏范数,不包含除法运算,易于工程实现。
1 归一化空时自适应抗干扰技术
空时自适应抗干扰技术通过时间抽头将一维的空域滤波推广到时间与空间的二维域中,形成空时二维处理结构[10],如图1所示。该结构在不增加阵元的前提下,增加阵的自由度,从而增加可以处理的干扰数目;同时,空时自适应技术对多径干扰、相干干扰有好的抑制效果,使自适应算法设计可以更加灵活、有效,增强抗干扰能力。
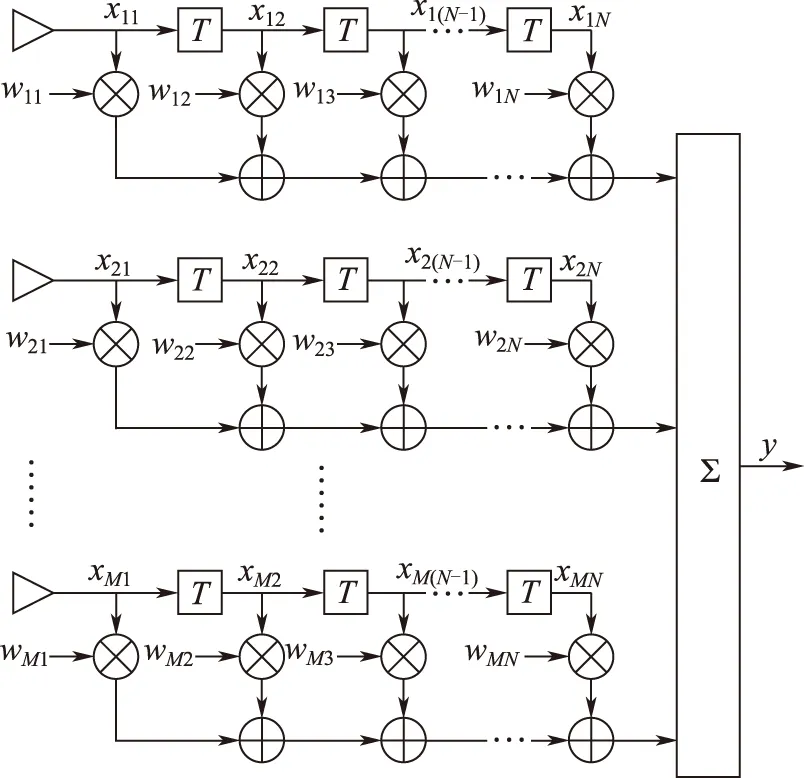
图1 空时自适应处理结构Fig.1 The structure of space-time adaptive processing
在空时自适应抗干扰技术标准形式中,n+1次迭代中应用于滤波器抽头权向量的失调包含以下三项[12]:
1)步长参数μ,由设计者控制;
2)抽头输入向量x(n),由信息源提供;
3)数据的估计误差e(n),为n次迭代计算的结果。
失调直接与抽头输入向量x(n)成正比,当x(n)较大时,梯度噪声放大,干扰抑制效果严重受损。
由Nagumo和Noda提出的归一化LMS抗干扰方法[13],n+1次迭代时抽头权向量的失调相对于n次迭代时抽头输入向量x(n)的平方欧氏范数进行归一化,可以有效克服这一问题,减轻梯度噪声放大,提高算法收敛速度。
归一化LMS抗干扰方法权值迭代如下
其中:w(n)表示第n个时刻处理器权矢量;w(n+1)表示第n+1个时刻处理器权矢量;μ为自适应常数;x(n)表示第n个时刻各通道输入向量;e*(n)表示数据估计误差复数共轭,e(n)=d(n)-wH(n)x(n),d(n)为第n个时间步的期望响应。
归一化LMS抗干扰方法尽管能带来好的抗干扰效果,但计算x(n)的平方欧氏范数的运算量增加显著,归一化处理过程中包含除法运算,不利于工程实现,尤其是FPGA实现。
2 基于FPGA实现的归一化空时自适应抗干扰技术
2.1 系统框图
基于FPGA实现的归一化空时自适应抗干扰技术,不需要计算x(n)的平方欧氏范数,不包含除法运算,通过主通道功率统计值调节步长因子,进行归一化处理,达到降低梯度噪声、提高收敛速度的目的。
基于FPGA实现的归一化空时自适应抗干扰技术系统原理图如图2所示,处理器权采集接收机各个通道收到的中频数据,支路1实时计算各通道输入信号功率,为简化运算或减少硬件资源占用率,可以只计算主通道或关键通道输入信号功率;支路2进行延时打拍形成空时二维处理结构X(n),MN×1维向量W(n)为
W(n)=Wq-CaWa(n)
(1)
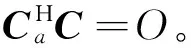
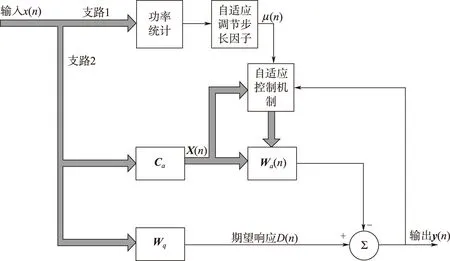
图2 基于FPGA实现的归一化空时干扰技术原理图Fig.2 The scheme of normalized space-time adaptive anti-jamming based on FPGA
2.2 自适应步长因子调节
通过迭代法进行自适应步长因子调节,计算第n个时刻的步长因子μ(n),μ(n)可表示为
μ(n)=a(n)·μ(1)
(2)
式中,μ(1)为第1个时刻的步长因子,预先给定;a(n)为自适应调节因子,采用式(3)选择a(n),使P′(n)近似等于期望功率P0:
(3)
式中,a(n)表示第n个时刻的自动调节因子,第1个时刻的自动调节因子a(1)预先给定;λ表示a(n)的调节步长,为预先给定的恒值;avg{·}表示对统计长度为sgn(a(n))的功率差的均值运算;P′(n)表示经调节后的第n个时刻的通道输入信号功率;P0为通道期望功率,依据系统硬件特性和使用环境预先给定;P(n)为第n个时刻的通道输入信号功率。
2.3 自适应权向量计算
采用式(4)计算自适应权向量Wa(n),Wa(n+1)表示第n+1个时刻的自适应权向量,Wa(n)表示第n个时刻的自适应权向量,第1个时刻的自适应权矢量Wa(1)预先给定
(4)
式中,Y(n)表示第n个时刻处理器输出。
2.4 期望响应计算
将接收机各个通道延时打拍后的中频数据X(n)与静止权向量Wq进行乘加运算得到期望响应d(n),d(n),如式(5)所示。
(5)
2.5 处理器输出计算
将接收机各个通道延时打拍后的中频数据X(n)与处理器权矢量W(n)进行乘加运算得到处理器输出Y(n),如式(6)所示。
(6)
3 仿真验证
仿真分析中,卫星接收天线选用实际工程应用中广泛使用的4阵元平面圆阵,阵元间距为卫星信号中心频率所对应的半波长,图3给出了阵元位置结构示意图。其中,位于坐标原点的阵元为主阵元,其余阵元间隔120°。
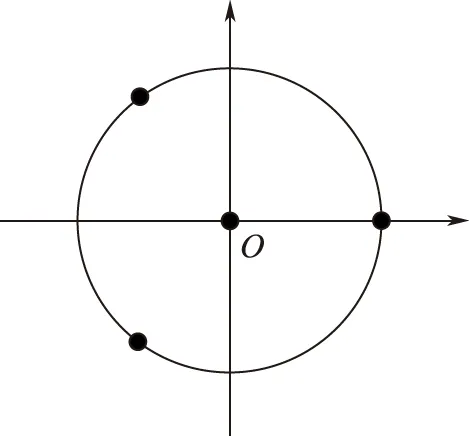
图3 阵元阵列示意图Fig.3 The schematic diagram of antenna array
干扰信号从方位角75°、俯仰角65°入射,图4(a)给出了归一化空时自适应抗干扰处理器输出Y(n)随迭代步数的变化情况;图4(b)给出了归一化空时自适应抗干扰处理器输出Y(n)稳定后的干扰抑制方向图。从图4(a)中可以看出,归一化空时自适应抗干扰处理器在很短的时间内即可收敛,达到稳定状态;从图4(b)中可以看出,方向图零陷方向与干扰来向一致。
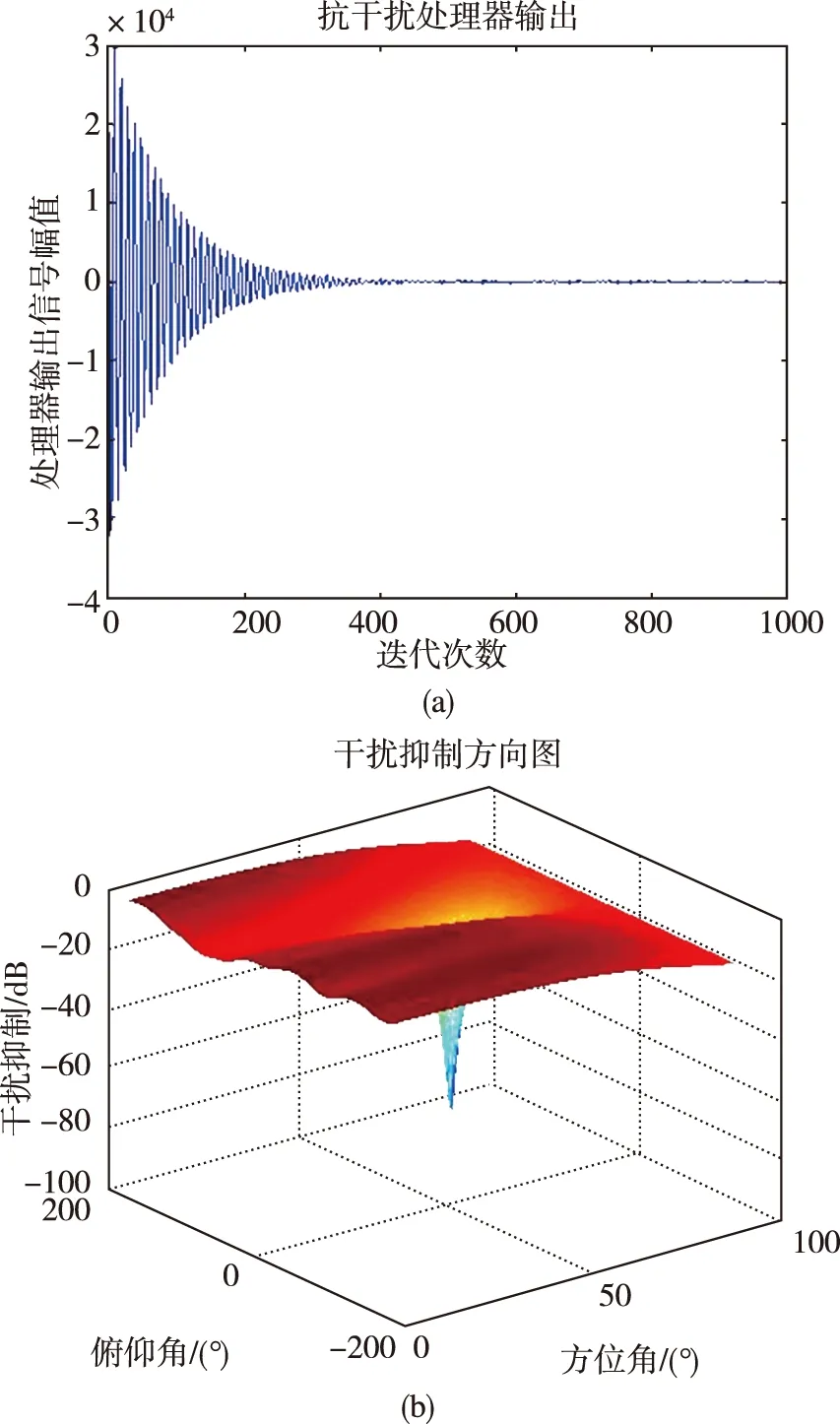
图4 干扰抑制仿真Fig.4 Simulation of the anti-jamming
试验验证中,选用4阵元平面圆阵卫星接收天线,施加20M带宽BPSK调制类型的宽带干扰,干扰到达卫星接收天线口面的强度约为95dB(AD采样幅值约±30000,即达到16位AD芯片临界值),对采用一般空时自适应抗干扰技术和采用归一化空时自适应抗干扰技术进行对比测试,并分别对处理器输出Y(n)进行ChipsCope抓图,如图5(a)、图5(b)所示,两种抗干扰方法都对干扰信号进行了有效抑制,处理器输出Y(n)分别为-1500~1500、-400~400。图5(a)与图5(b)对比,可以看出采用归一化空时自适应抗干扰技术处理器输出信号(图5(b))更平稳、幅值更小,达到了降低梯度噪声的目的,对于强干扰,噪声抑制的效果更加明显。
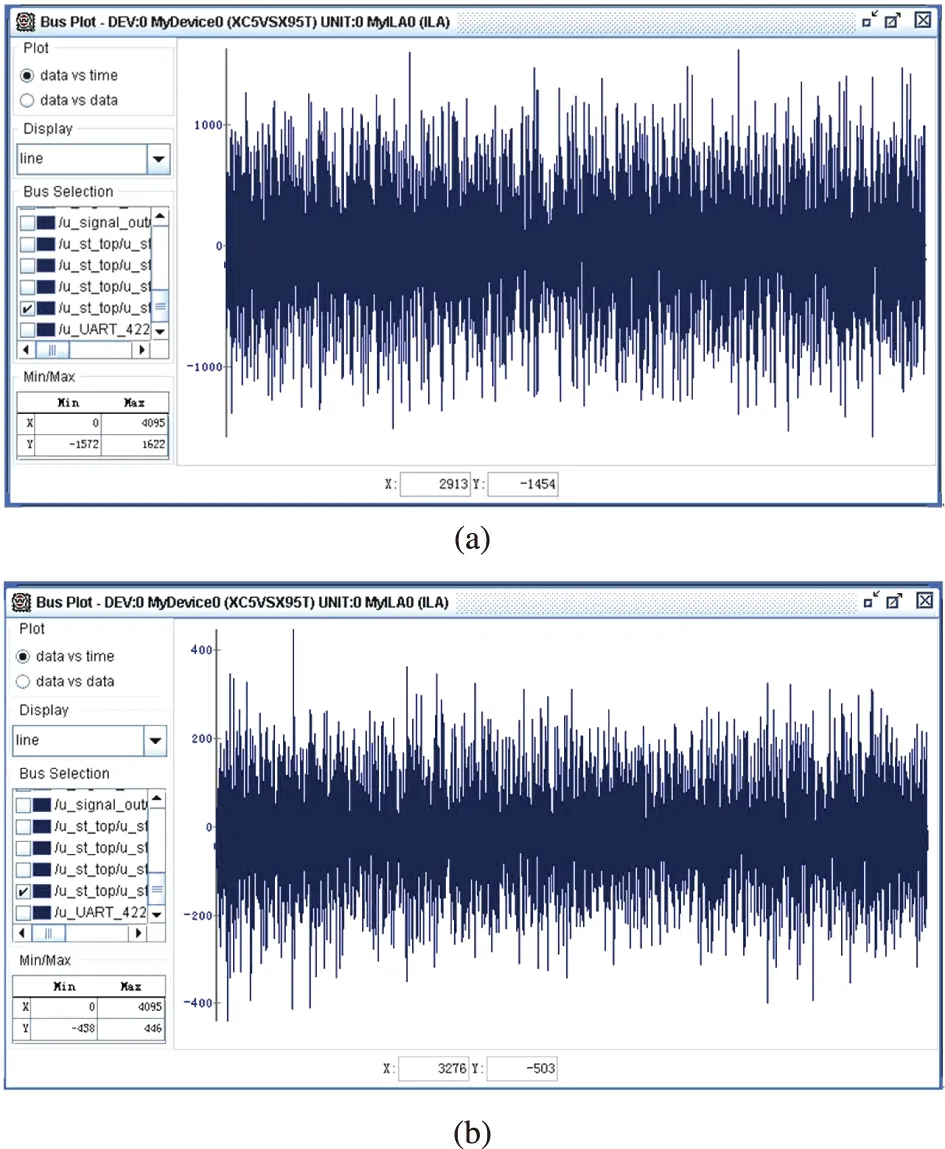
图5 空时自适应处理器输出ChipsCope抓图Fig.5 The ChipsCope diagram of the space-time adaptive processor output
4 结论
本文提出一种基于FPGA实现的归一化空时自适应抗干扰技术。通过主通道功率统计值调节步长因子,达到归一化处理的目的,当x(n)较大时,可以解决梯度噪声放大的问题,有效地提高了算法的抗干扰能力;不需要计算u(n)的平方欧氏范数,不包含除法运算,减少了计算量,易于FPGA工程实现;通过计算机仿真分析和外场试验验证了该技术有效地提高了算法收敛速度和干扰抑制能力。
[1]SvendsenAS,GuptaIJ.AdaptiveantennaforhandheldGPSreceivers[A].2010IEEE/IONPositionLocationandNavigationSymposium(PLANS)[C].IndianWells,CA,USA,2010:436-442.
[2]LiM,DempsterAG,BalaeiAT,etal.Switchablebeamsteering/nullsteeringalgorithmforCWinterferencemitigationinGPSC/Acodereceivers[J].IEEETransactionsonAerospaceandElectronicSystems,2011,47(3):1564-1579.
[3]XiaoH,LamareRC.Reduced-rankspace-timeadaptiveinterferencesuppressionfornavigationsystemsbasedonQRdecompositionandapproximationsofbasisfunctions[J].InternationalJournalofCommunicationSystems,2012,25(25):616-635.
[4] 武成锋,彭元,何子君,付晶晶.卫星导航干扰与抗干扰技术综述[J].导航定位与授时,2014,1(2):57-63.
[5]FanteRL,VaccaroJJ.WidebandcancellationofinterferenceinaGPSreceivearray[J].IEEETransactionsonAerospaceandElectronicSystems,2000,36(2):549-564.
[6]MyrickWL,GoldsteinJS,ZoltwskiMD.Lowcomplexityanti-jamspace-timeprocessingforGPS[A].2001IEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing[C]. 2001:2233-2236.
[7]SklarJR.Interferencemitigationapproachesfortheglobalpositioningsystem[J].LincolnLaboratoryJournal,2003,14(2):167-180.
[8]WernerS,WithM,KoivunenV.Householdermultistagewienerfilterforspace-timenavigationreceivers[J].IEEETransactionsonAerospaceandElectronicSystems,2007,43(3):975-988.
[9]SrinivasanR,RangaswamyM.FastestimationoffalsealarmprobabilitiesofSTAPdetectorstheAMF[C].ProceedingsoftheIEEEInternationalRadarConference,Arlington,VA,May9-12,2005.
[10] 郭艺.GPS接收机空时抗干扰理论与实现关键技术研究[D].长沙:国防科技大学,2007.
[11]RodrigoCDeLamare,RaimundoSampaio-Neto.Reduced-rankspace-timeadaptiveinterferencesuppressionwithjointiterativeleastsquaresalgorithmsforspread-spectrumsystems[J].IEEETransactionsonVehicularTechnology,2010,59(3):1217-1228.
[12] 王永良,丁前军,李荣锋.自适应阵列处理[M].北京:清华大学出版社,2009:73-80.
[13] 西蒙·赫金.自适应滤波器原理(第四版)[M].北京:电子工业出版社,2010:251-267.
A Realization of Normalized Space-time Adaptive Anti-jamming Based on FPGA
FU Jing-jing,LI Feng,WU Cheng-feng,HE Zi-jun
(Beijing Institute of Automatic Control Equipment,Beijing 100074,China)
This paper represented a normalization STAP(Space-Time Adaptive Processing)Anti-jam technology base on FPGA realization.Using frequency statistical information of major channel adjusts step-factor.Realizing normalization process has two advantages.First,When the value ofx(n)islarge,theproblemofgradientnoiseamplificationwillbesolved,andtheperformanceofanti-jamwillbeimprovedeffectively.Second,thesquareEuler-normofu(n)willnotbecalculated,soitisofsimplecalculationandeasyrealizationonFPGA.Thoughthesimulationanalysisbycomputerandtheresultofrealtesting,thenormalizationprocessimprovethespeedofarithmeticconvergenceandtheperformanceofanti-jameventually.
Normalization;STAP;Anti-jamming
2015-12-14;
2016-01-28。
付晶晶(1982-),女,硕士,主要从事卫星导航抗干扰算法与实现研究。
TP
A
2095-8110(2016)02-0048-05
