导引头耦合度对控制系统影响机理分析
2016-03-16陈林华
朱 伟,吴 刚,陈林华
(航天科工四院九部,武汉 430040)
导引头耦合度对控制系统影响机理分析
朱 伟,吴 刚,陈林华
(航天科工四院九部,武汉 430040)
以经典三环控制结构自动驾驶仪、纯比例导引律为例,从自动驾驶仪的角度分析了导引头耦合度(隔离度)对控制系统的影响。耦合度通过改变自动驾驶仪内部的结构参数,极大地影响了控制系统性能,从而引发一系列其他相关问题。
导引头;隔离度;自动驾驶仪
0 引言
在准确打击移动目标领域,很多武器采用了随动导引头、比例导引法末制导模式。但此模式下过大的导引头耦合度对控制系统的影响很大,较大程度地限制了控制系统设计的自由度,所以有必要对其进行详细的机理分析。
目前相关文献,基本上均是将自动驾驶仪等效为一个固定传递函数,然后从制导回路分析耦合度对制导系统的影响,然后通过串联校正网络(制导滤波器)进行校正来削弱耦合度的不利影响。关于再进一步深入分析的文献不多,故有必要从另外的角度分析耦合度对控制系统的影响,达到简化设计流程和设计难度的目的。
本文从自动驾驶仪的角度分析了导引头耦合度对控制系统的影响,得到的结论是:导引头耦合度通过改变经典的三环自动驾驶仪内部的结构参数,极大地影响其性能,从而引发一系列的问题。
另外,从自动驾驶仪角度分析问题的另一个优势是,能够直接得到确切的控制系统性能,可以更为方便地进行系统回路的分析和设计。
1 自动驾驶仪
自动驾驶仪的主要作用有两个:一个是复现导引指令,使得导弹能够准确命中目标;而另一个就是校正弹体性能,避免在飞行过程中姿态发散。下面以弹体性能最为不利的情况——静不稳定弹体为例,进行相关理论分析。
由于被控对象是静不稳定弹体,故在自动驾驶仪中需要引入角速率积分环节。为据代表性,下面以经典带伪姿态角的三环控制器来进行理论分析。控制框图如图1所示。

图1 三环控制器结构示意图Fig.1 Diagram of classical three loop autopilot(TLA)
图1中,1/s表示积分器。kn、ki、kw分别为外环、中环、内环控制参数,在某个飞行特征点上为定值。
kw为姿态阻尼控制参数,主要作用是调节自动驾驶仪中姿态的阻尼特性;
ki为姿态比例控制参数,主要作用是校正静不稳定弹体对自动驾驶仪的影响,提升低频幅值裕度;
kn为过载占比参数,主要用于调节过载回路在自动驾驶仪中的占比特性;
这里,为更好地理解kn,笔者将其换一个称呼:自动驾驶仪隔离度参数。
由此可以看出,自动驾驶仪的职能有两个方面,姿态角速率性能和速度角速率性能(为简洁起见,本文此后出现的“过载”均指速度角速率)。一般而言,分析控制系统时,只考虑自动驾驶仪的过载性能(外环);而在分析稳定系统时,对自动驾驶仪的姿态性能(中环和内环)关注更多。
自动驾驶仪中,kw和ki决定了整个自动驾驶仪的姿态性能特性,而kn意味着划分出一定的比例给过载回路;kn越大,则划出的比例越多;kn越小,则留给姿态回路的越多。
2 导引头耦合度影响机理分析
由于导引头内部随动系统快速性以及头罩斜率等因素的影响,在导引头提供的视线角速率中包含了一定量的弹体角速率信息。将其在全部的弹体角速率中所占的比例定义为导引头的耦合度A。在当前的工艺条件下,一般均可达到±4%以内。简化模型如图2所示。

图2 导引头耦合度结构示意图Fig.2 Diagram of seeker disturbance rejection rate
这里以纯比例导引律为例:
(1)
假设导引头耦合度为A,将耦合弹体角速率等价移至自动驾驶仪内部中环,则图1可演变为图3,进一步可将其等价变化为图4。
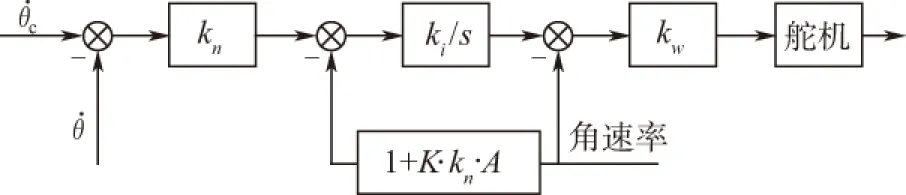
图3 考虑导引头耦合度的三环控制器结构示意图Fig.3 Diagram of TLA (considering seeker disturbance rejection rate)
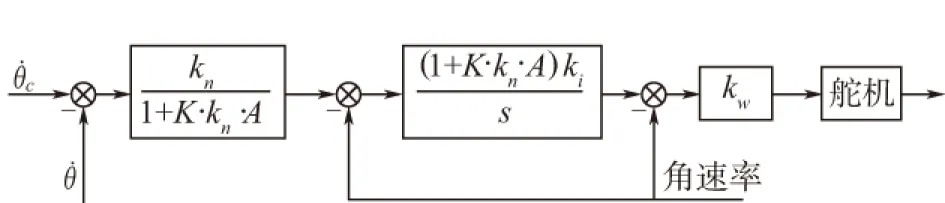
图4 考虑导引头耦合度的三环控制器结构示意图(等价变化后)Fig.4 Diagram of TLA(considering the disturbance isolation index of seeker)
从图 4可以看出,在导引头耦合度的影响下,自动驾驶仪引入了一个畸变参数Ka=1+K·kn·A,使得中环系数和外环系数变为:
Ki=ki·Ka=ki·(1+K·kn·A)
(2)
参考图4,可以得到以下结论:
1)当A=0时,畸变参数Ka=1,自动驾驶仪未发生变化;
2)当A=-1/(K·kn)时,则畸变参数Ka=0、中环系数Ki=0,意味着伪姿态角反馈完全不起作用;
3)假设A继续负向增长,伪姿态角反馈变为正反馈,进一步恶化自动驾驶仪的稳定性,就算是静稳定弹体都有可能姿态发散;
4)当A>0时,Ka>1,相比较畸变以前,中环系数放大,外环系数缩小,表明过载在自动驾驶仪中占比减小,对于制导系统而言,意味着自动驾驶仪变得更为“迟钝”,快速性降低。另一方面,由于放大了中环系数,将会恶化舵系统间隙引发的姿态极限环振荡。
假设导航比K=4,在A=-4%和A=-8%的情况下,Kn和Ka随kn大小变化见图5~图8。从图可以看出:
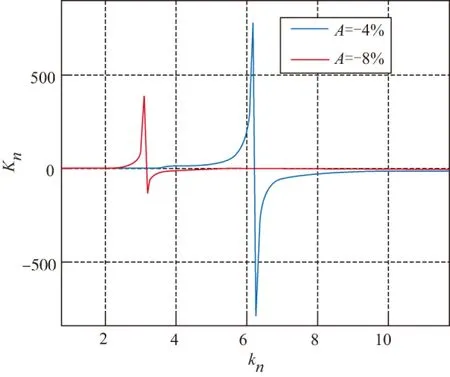
图5 A<0时,Kn随kn大小变化图Fig.5 When A<0, diagram of Kn VS kn

图6 A<0时,Ka随kn大小变化图Fig.6 When A<0, diagram of Ka VS kn
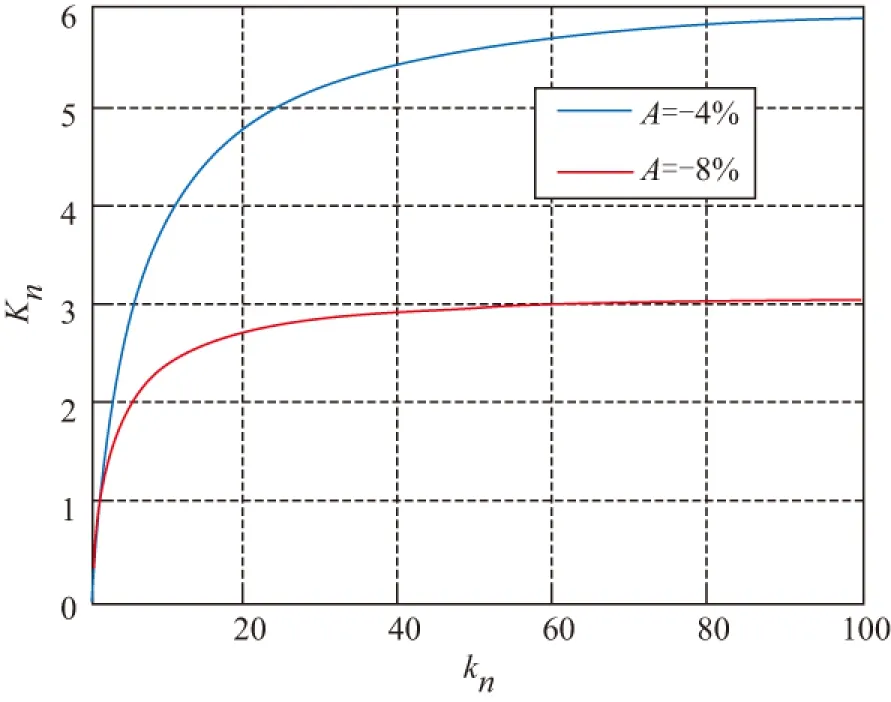
图7 A>0时,Kn随kn大小变化图Fig.7 When A>0, diagram of Kn VS kn

图8 A>0时,Ka随kn大小变化图Fig.8 When A>0, diagram of Ka VS kn
1)当耦合度为负值时,Ka会出现零点;
2)无论耦合度正负,Kn随着kn增大而出现饱和特性,饱和极限值为1/(K·A)。
3 解决措施
从以上分析可以看出,导引头耦合度对控制系统的影响,主要是对自动驾驶仪的影响。其核心在于畸变参数Ka。为了减小自动驾驶仪的畸变程度,保持原始的设计结果,必须将畸变参数Ka限制在1附近。参考定义式Ka=1+K·kn·A,解决的途径就是尽量将K·kn·A限制为零,即需要对K、kn、A进行量值分配,综合减小K·kn·A的量值;而不是单独的压制某个参数来满足系统要求。
A是导引头耦合系数,是评判随动导引头优劣的一个重要指标。导引头系统设计师的一个重要工作内容,就是利用头罩补偿技术、提升伺服系统性能等手段,尽量减小其变化范围。
K是制导回路导航比,一般而言必须大于2,通常取值为3~5。
kn是自动驾驶仪的外环系数,或者过载占比系数,描述了过载快速性在姿态快速性中的占比关系。量值越大,自动驾驶仪的快速性(过载性能)越好;量值越小,自动驾驶仪(过载性能)越“迟钝”。需要注意的是,kn的减小并没有降低自动驾驶仪中的姿态快速性,甚至因为在减小了制导系统的干扰后,稳定系统的稳定性会表现得更好。
在这里,只考虑自动驾驶仪方面的设计思路。
在对kn的设计中,攻角到弹道倾角的简化传递函数为
(3)
不管采用何种设计理念,均可归结为如下公式,不同的只是Kc的取值问题。
(4)
其中,c1为弹体升力系数,表征了单位攻角产生的速度旋转速率。于是得到
K·kn·A=K·Kc·A·Tc
(5)
从公式可以得到以下结论:
1)K和Kc是自动驾驶仪的设计参数,它们的量值大小决定了命中精度大小;所以规划时需注意,在攻击末端的一段时间内,必须将两者提升至符合制导收敛性,否则脱靶量必不满足要求;
2)提升弹体升力系数c1可有效抵消导引头耦合度A变化范围;或者说,当固定A的变化范围后,提升弹体升力系数c1可等比例地提升K·Kc的取值,提高命中精度;
3)当弹体升力系数c1很小,而导引头耦合度A变化范围又很大,则必然将K和Kc限制在一个很小的值,在保证自动驾驶仪稳定性的基础之上,命中精度必然无法满足要求;
4)在此,自动驾驶仪的设计其实就是均衡命中精度与抗导引头耦合度A鲁棒性之间的矛盾;
5)由于弹体升力系数c1正比于动压,所以也可采用K和Kc正比于动压的规划策略;
6)在弹目交汇前的一段时间内,必须要保证一定程度的动压;但是过高的动压会提升稳定系统的设计难度。
4 自动驾驶仪设计示例
为了更为清晰地描述耦合度对自动驾驶仪的影响机理,同时也可表明气动性能对系统的影响,特选取了两个大小不一的升力系数,分别进行分析。考虑导引头耦合度A=±4%。
以静不稳定弹体的某个特征点为例,其动力系数如下:b1=0.01,b2=-100,b3=100;c1=0.5;c3=0.1;
而另一个特征点除了c1=0.2,c3=0.04外,其他力系数完全等同上一个特征点,即b1=0.01,b2=-100,b3=100。
4.1 考虑耦合度前的名义设计
4.1.1 大升力系数
未考虑导引头耦合度A时,自动驾驶仪名义设计结果如图9、图10所示。

图9 自动驾驶仪名义设计结果(角速率)Fig.9 Nominal design for autopilot(Attitude rate)

图10 自动驾驶仪名义设计结果(过载)Fig.10 Nominal design of autopilot(Overload)
图中:角速率回路下限幅值裕度为-7.98dB,上限幅值裕度为13dB,相位裕度为49.8°,剪切频率为26.7rad/s。过载回路下限恒稳定,上限幅值裕度也为18dB,相位裕度为88.4°,剪切频率为2.58rad/s。
此时,kw=0.3,ki=10;kn=3;即Kc=1.5。
4.1.2 小升力系数
未考虑导引头耦合度A时,自动驾驶仪名义设计结果如图11、图12所示。

图11 自动驾驶仪名义设计结果(角速率)Fig.11 Nominal design for autopilot(Attitude rate)

图12 自动驾驶仪名义设计结果(过载)Fig.12 Nominal design for autopilot(Overload)
图中:角速率回路下限幅值裕度为-7.92dB,上限幅值裕度为13dB,相位裕度为50.1°,剪切频率为26.7rad/s。过载回路下限恒稳定,上限幅值裕度也为17.6dB,相位裕度为76.1°,剪切频率为2.65rad/s。
从设计结果上来看,性能几乎完全等同大升力系数状态的情况。此时,kw=0.3,ki=10,Kc=1.5,均保持不变,但是kn放大了2.5倍,即kn=7.5。
4.2 正耦合度的畸变结果
4.2.1 大升力系数
当考虑导引头耦合度A=4%时,则Ki=14.8,Kn=2.027;稳定性能如图13、图14所示。

图13 考虑耦合度4%时的自动驾驶仪性能图(角速率)Fig.13 Considering A=4%,Nominal design for autopilot(Attitude rate)

图14 考虑耦合度4%时的自动驾驶仪性能图(过载)Fig.14 Considering A=4%,Nominal design for autopilot(Overload)
从图看出,由于Ki的畸变放大,角速率回路的下限幅值裕度提升至-10.9dB,但是相位裕度降低了8.2°。而过载回路的快速性(剪切频率)下降了近一半。
4.2.2 小升力系数
当考虑导引头耦合度A=4%时,则Ki=22,Kn=3.41;稳定性能如图15、图16所示。
从图看出,由于Ki的畸变放大,角速率回路的下限幅值裕度提升至-14dB,但是相位裕度降低了17.9°。而过载回路的快速性(剪切频率)只剩下了三分之一。

图15 考虑耦合度4%时的自动驾驶仪性能图(角速率)Fig.15 Considering A=4%,Nominal design for autopilot(Attitude rate)

图16 考虑耦合度4%时的自动驾驶仪性能图(过载)Fig.16 Considering A=4%,Nominal design for autopilot(Overload)
4.3 负耦合度的畸变结果
4.3.1 大升力系数
当考虑导引头耦合度A=-4%时,则Ki=5.2,Kn= 5.7692;稳定性能如图17、图18所示。
从图看出,由于Ki的畸变减小,角速率回路的下限幅值裕度缩减至-3.03dB。而过载回路的快速性(剪切频率)上升了近1倍。
4.3.2 小升力系数
当考虑导引头耦合度A=-4%时,则Ki=-2,Kn=-37.5000;稳定性能如图19、图20所示。从图看出,由于Ki的畸变减小,变为负值,而此时弹体是静不稳定的,整个自动驾驶仪失稳。

图17 考虑耦合度-4%时的自动驾驶仪性能图(角速率)Fig.17 Considering A=-4%,Nominal design for autopilot(Attitude rate)

图18 考虑耦合度-4%时的自动驾驶仪性能图(过载)Fig.18 Considering A=-4%,Nominal design for autopilot(Overload)

图19 考虑耦合度-4%时的自动驾驶仪性能图(角速率)Fig.19 Considering A=-4%,Nominal design for autopilot(Attitude rate)

图20 考虑耦合度-4%时的自动驾驶仪性能图(过载)
Fig.20 ConsideringA=-4%,Nominal design for autopilot(Overload)
4.4 设计小结
从上面的设计示例可以看出,小升力系数状态下的名义设计必须重新进行,将名义kn大幅减小从而减低畸变参数Ka,才能满足抗耦合度A=±4%范围的鲁棒性。但是过小的kn必然无法满足命中精度的要求。
换而言之,过载占比参数kn的名义取值必须受到耦合度变化范围以及升力系数大小的限制,不可设计过大。当耦合度变化范围较大的同时升力系数过小,将会极大地限制自动驾驶仪的设计,甚至会出现设计无解的极端情况。
导航比K也具有与kn类似的情况。
5 结束语
本文从自动驾驶仪的角度分析导引头耦合度对控制系统的影响。相比较传统的制导回路分析思路,本文提供的分析方法帮助控制系统设计人员能够从另一个方位认识导引头耦合度对控制系统的影响,为更进一步完善设计结果提供参考。
另外,本文未考虑导引头耦合度更为详细的复杂模型。此方面的研究将作为下一步的主要分析方向和内容。
[1] 赵善友.防空导弹武器寻的制导控制系统设计[M].北京:宇航出版社,1992:136-140.
[2] Nesline F W,Zarchan P.Radome induced miss distance in aerodynamically controlled homing missiles[J].AIAA 84-1845,1984:99-115.
[3] 崔莹莹, 夏群力, 祁载康.导引头稳定平台隔离度模型研究[J].弹箭与制导学报, 2006, 26(1): 22-25.
[4] 徐平, 王伟, 林德福.导引头隔离度对末制导炮弹制导控制的影响[J].弹道学报, 2012, 24(1): 17-22.
[5] 杜运理, 夏群力, 祁载康.导引头隔离度相位滞后对寄生回路稳定性影响研究[J].兵工学报, 2011, 32(1): 28-33.
The Influence Mechanism Analysis of Seeker Disturbance Rejection Rate on Control System
ZHU Wei,WU Gang,CHEN Lin-hua
(The 9th Designing of China Aerospace Science Industry Corp,Wuhan 430040,China)
With the classical three loop autopilot(TLA) and pure proportional navigation guidance law, the influence mechanism of seeker disturbance rejecion rate on control system is analyszed from the perspective of autopilot.The study shows that seeker disturbance rejection rate will greatly influence the performance of control system by changing its structure parameters and cause serie of related problems.
Seeker;Disturbance rejection rate;Autopilot
10.19306/j.cnki.2095-8110.2016.03.008
2015-04-02;
2015-06-25。
朱伟(1980-),男,主要从事控制理论方面的设计和研究。
TJ765.3
A
2095-8110(2016)03-0044-07
