地空导弹行进间稳定发射平台技术研究

马志刚，罗 刚，尹康军

(中国人民解放军驻三六五五厂军事代表室，贵州 遵义 563000)

地空导弹行进间稳定发射平台技术研究

马志刚，罗 刚，尹康军

(中国人民解放军驻三六五五厂军事代表室，贵州 遵义 563000)

通过对地空导弹行进间稳定发射平台进行技术研究，重点解决行进间发射平台的姿态测量精度和动态水平稳定控制等技术难题，为行进间发射导弹提供稳定的发射平台。

地空导弹；发射平台

0 引言

科技的迅猛发展使防空作战环境更为复杂，既要求武器系统有快速反应能力，又要求作战方法由静止战向机动灵活的运动战转变。美军《联合作战设想》提出“武器系统既能在停止时使用，也能在运动中使用，持续机动的火力作战效能最大”，这反映了美军作战原则的新变化。高技术局部战争节奏快、强度高、密度大，导弹战成为作战主要方式之一，侦察技术的发展和打击精度的提高，要求导弹武器系统具备快速准备、快速发射和较强生存保障能力。为适应这一要求，具有大功率自适应能力的地空导弹行进间稳定发射平台应运而生。

本文通过对地空导弹行进间稳定发射平台进行技术研究，重点解决行进间稳定发射平台的姿态测量精度和动态水平稳定控制等技术难题，为行进间发射导弹提供稳定的发射平台。发射平台能在行驶状态下进行自适应控制并保持导弹发射时的高精度水平稳定，在方位上具有快速回转功能，实现行进中导弹发射的快速瞄准，从而较好地解决行进中发射导弹的难题，为发射车实施“即停即射”或行进中发射导弹创造了良好的条件，使地空导弹武器系统具有反应快、机动性强、自动转移火力、边走边打的能力。

1 组成及工作原理

1.1 组成

地空导弹行进间稳定发射平台主要由捷联惯性测量组合(IMU)、控制计算机、伺服控制器、伺服电机、传动机构、回转装置及稳定平台等组成。系统组成框图如图1所示。

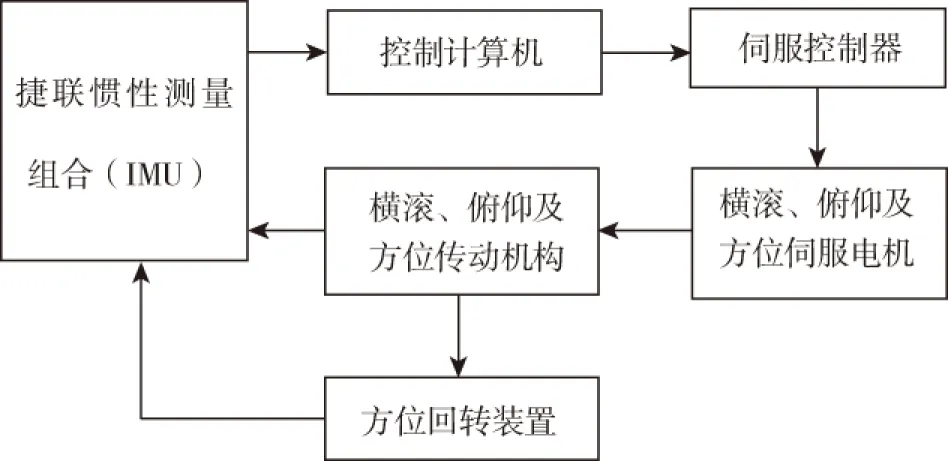
图1 系统组成框图Fig.1 System composition block diagram

1.2 工作原理

图2 系统原理框图Fig.2 System principle block diagram

2 关键技术研究

发射平台横滚角、俯仰角和方位角的角度测量，若在静态情况下，可用倾角传感器；但在行驶中倾角传感器由于受到加速度等各种干扰，倾角传感器的输出值将严重失真，不能真实地反应发射平台的姿态角，即横滚角、俯仰角和方位角。发射平台采用捷联惯性测量技术构建“数学平台”，解算行进中发射平台的姿态角，采用多种误差修正算法，消除测量误差。同时，应用智能伺服控制技术[2]，采用广义预测控制算法，实现发射平台的智能预测自适应控制，根据所测得的平台姿态角，控制发射平台的横滚角、俯仰角和方位角的伺服系统，使平台在行进中始终保持一定的水平精度，并根据控制计算机的输入信息进行方位快速同步跟踪瞄准。

2.1 “数学平台”的构建及误差修正

将惯测组合IMU(陀螺仪和加速度计)直接固联在平台上。惯测组合测得沿敏感轴相对于惯性空间的角速率和加速度分量，陀螺仪和加速度计输出的信息经误差补偿，分别送入姿态矩阵计算和由载体坐标系至平台坐标系的方向余弦矩阵的计算，利用姿态矩阵的元素，提取姿态和方位信息。姿态矩阵计算、加速度信息的坐标变换、姿态和方位的计算构成“数学平台”。由于捷联惯导系统不存在平台惯导中的施矩量受物理条件限制的问题，因此捷联惯导系统的测量坐标系取为地理坐标系。计算框图如图3所示。

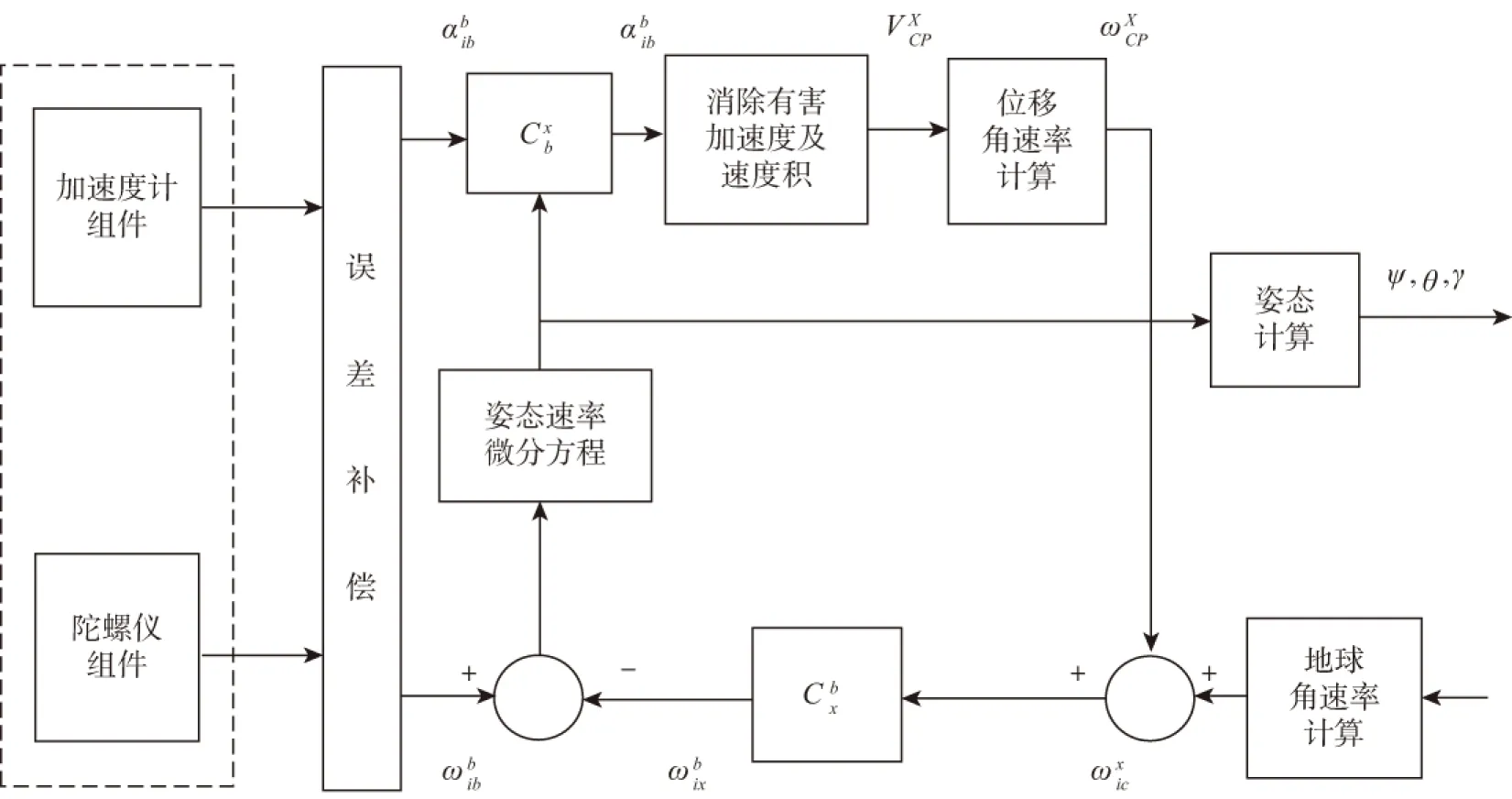
图3 测量计算框图Fig.3 Measuring calculation diagram

为了消除测量误差，采用加速度计误差补偿、陀螺误差补偿、车辆测速仪修正、零速停车修正和粗精对准等多种技术实现系统误差补偿[3]，确保发射平台姿态测量精度。

2.2 伺服控制系统

控制系统主要由IMU、伺服控制器、伺服电动机、方位角传感器、传动机构等组成。伺服控制系统组成框图如图4所示。

图4 伺服控制系统组成框图Fig.4 Servo control system composition block diagram

伺服控制器接收控制计算机的控制信息(控制计算机通过测量计算所得的平台当前的横滚角γ、俯仰角θ和方位角ψ)，根据平台姿态控制目标(如使横滚角γ、俯仰角θ角度值始终趋于零，而方位角ψ与目标同步跟踪)计算系统失调角ek，再进行校正环节的运算得到当前控制值uk；由当前控制值uk转换为PWM脉宽占空比，从而产生脉宽PWMk控制信号；同时，采集电动机转子位置信息，并结合当前控制值uk的控制方向计算出控制IGBT信息，实现控制脉宽PWMk对6个IGBT的有效控制，从而最终实现系统的伺服控制功能。

2.3 预测控制算法模型建立

通常预测控制算法主要有基于非参数模型的模型算法控制(MAC)、动态矩阵控制(DMC)和基于参数模型的广义预测控制(GPC)、广义预测极点配置控制(GPP)等,其中模型算法控制采用对象的脉冲响应模型，动态矩阵控制采用对象的阶跃响应模型，这两种模型具有易于获得的优点；广义预测控制和广义预测极点配置控制是预测控制思想与自适应控制的结合，采用CARIMA模型，具有参数数目少并能够在线估计的优点，而广义预测极点配置控制进一步采用极点配置技术，提高了预测控制系统的闭环稳定性和鲁棒性。因此本文采用广义预测控制算法，实现发射平台的智能预测自适应控制[4]。

2.3.1 广义预测控制算法预测模型

预测模型具有预测的功能，即能够根据系统的历史数据和未来的输入，预测系统未来输出值。采用CARIMA(受控自回归积分滑动平均模型)作为预测模型。模型表达式为

A(z-1)y(k)=B(z-1)u(k-1)+C(z-1)ξ(k)/Δ

(1)

式中：A(z-1)、B(z-1)、C(z-1)分别为n、m和n阶的z-1的多项式；Δ——Δ=1-z-1；y(k)——输出；u(k)——输入；ξ(k)——零均值白噪声。

2.3.2 滚动优化

(1)目标函数

为增强系统的鲁棒性，在目标函数中考虑现在时刻的控制u(k)对系统未来时刻的影响，其目标函数为

(2)

式中：n——预测最大长度；m——控制长度，m≤n；λ(j)——控制加权系数，大于零，这里取λ(j)=λ(常数)。

对设定值进行柔化处理，得到参考轨迹

w(k+j)=αjy(k)+(1-αj)yr(j=1,2…，n)

式中：yr、y(k)、w(k+j)分别为设定值、输出值和参考轨迹；α——柔化系数，0<α<1。

其预测控制问题，就是通过优化求得Δu(k),Δu(k),…,Δu(k+m-1)，使得目标函数J达到最小值。

(2)预测输出

根据预测理论，进行j步预测输出，可引入丢番图方程

1=Ej(z-1)A(z-1)+z-jFj(z-1)

(3)

式中：Ej(z-1)=ej0+ej1z-1+…ej,j-1z-j+1,ej0=1；Fj(z-1)=fj0+fj1z-1+…fjnz-n。

得到最优输出预测值为

(4)

(3)最优控制

设参考轨迹为

W=[w(k+1),w(k+2),…,w(k+n)]T

则目标函数可表示为

J=(Y-W)T(Y-W)+λΔUTΔU

(5)

将式(4)代入式(5)

ΔU=(GTG+λI)-1GT(W-f)

(6)

在实际控制时，仅仅将第一个控制分量加入系统中，有

u(k)=u(k-1)+gT(W-f)

式中，该gT为(GTG+λI)-1GT的第一行。

广义预测控制算法与通常的最优控制不同，采用滚动优化，优化目标是随时间推移的，在每个时刻都提出一个立足于该时刻的局部优化目标，而不是采用不变的全局优化目标。因此，优化过程不是一次离线完成的，而是在线反复进行的，这就是滚动优化目标的局部性，使得在理想条件下，只能取得全局的次优。但是，当模型失配或控制对象时变、非线性及干扰影响时，广义预测控制算法能够解决这种不确定性，及时进行补偿，减小偏差，保持实际的最优。

2.3.3 隐式广义预测自校正控制算法

(1)并列预测器

GPC的最优控制律如下

ΔU=(GTG+λI)-1GT(W-f)

式中，控制量加权因子λ和柔化后的设定值向量W已知，因此要求取ΔU，必须已知矩阵G和开环预测向量f。隐式自校正方法就是利用输入和输出数据，根据预测方程直接辨识G和f。

根据式(4)可得到n个并列预测器为

(7)

式中，矩阵G中所有元素g0、g1、…、gn-1都在最后一个方程中出现，因此仅对式(7)的最后一个方程进行辨识，即可求得矩阵G。

(2)矩阵G的求取

式(7)的最后一个方程为

y(k+n)=gn-1Δu(k)+…+g0Δu(k+n-1)+

f(k+n)+Enξ(k+n)

(8)

令

X(k)= [Δu(k),Δu(k+1),…,

Δu(k+n-1),1]

θ(k)=[gn-1,gn-2,…,g0,f(k+n)]T

则式(8)可写为

y(k+n)=X(k)θ(k)+Enξ(k+n)

(9)

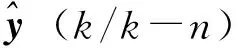
(10)

θ(k)采用以下递推最小二乘法公式进行估计：

(11)

式中，λ1为遗忘因子，λ1∈(0,1)。

由此得到k时刻n步估计值:

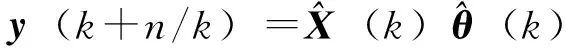
Δu(k+n-1),1]。

(3)预测向量f的求取

根据GPC与DMC控制规律的等价性，GPC中的f向量与DMC中的Y0向量相等，DMC的误差校正表达式为：

(12)

由式(12)得到下一时刻的Y0向量为

(13)

式中：p——模型时域长度(p≥n)；h2,h3,…,hp——误差校正系数，取h2,h3,…,hp为1；

e(k+1)——预测误差，e(k+1)=y(k+1)-y(k+1/k)。

因f与Y0等价，由式(13)可得到下一时刻的预测向量f

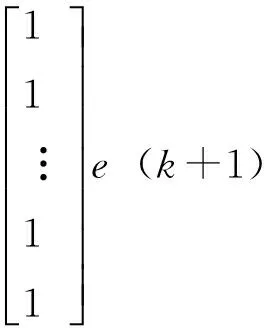
(14)

由此就求得了f向量。

由式(11)、式(14)计算得到G和f后，就可采用式(5)计算控制量。每一次计算，都可得到k时刻及以后n步的n个控制序列。为了及时地利用反馈信息决定控制量，每次计算完毕后，仅将控制序列中的第一个控制量作用于系统。

2.4 多自由度大承载稳定平台结构

地空导弹行进间稳定发射平台结构如图5所示。图5中,1是车体安装面；2是固定支座；3是外环，用于实现平台绕纵轴转动；4是纵摇电机及减速器，用于实现平台的俯仰控制；5是内环，用于实现平台绕横轴转动；6是设备安装平台，根据使用要求用于安装所需设备；7是横摇电机及减速器，用于实现发射平台的横滚控制；8是惯测组合，用于测量运动载体的加速度和姿态角速率；9是方位回转电机及减速器，用于实现发射平台的方位转动；10是锁紧机构，用于车辆在行驶中平台不需要调整时的锁紧固定。

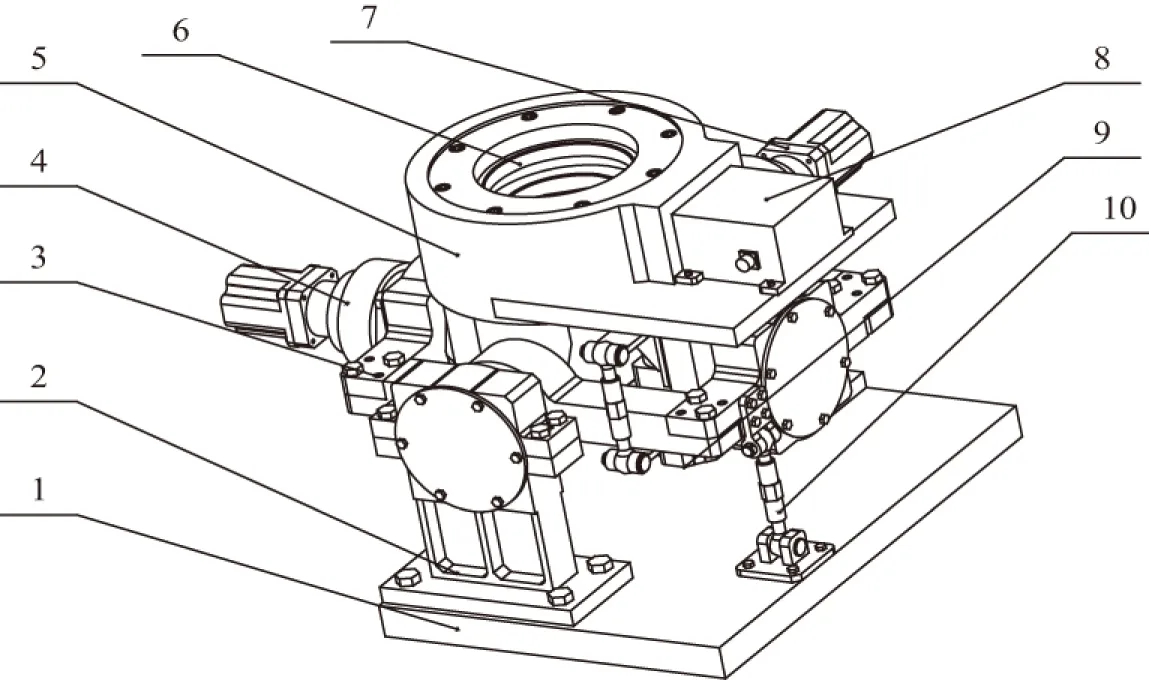
图5 平台机械结构图Fig.5 Mechanical structure drawing of the launch platform

平台能实现纵摇、横摇和方位旋转多个自由度运动。其工作原理是：纵摇运动过程是纵摇电机4带动其减速器运转，再带动内环5围绕其安装于外环的转轴转动；横摇运动过程是横摇电机7带动其减速器运转，再带动安装于固定支座2的转轴转动；方位运动过程是方位电机9带动其减速器运转，再带动方位回转齿圈转动，从而带动安装设备的方位回转运动。

2.5 软件

软件主要实现人机界面、导航计算及伺服控制[5]。

人机界面主要实现原始数据输入、导航控制、平台伺服控制。

导航计算主要实现实时采集各种传感器的数据、初始对准计算、利用IMU进行导航计算、零速修正、记录与保存数据。

伺服控制主要实现接收控制计算机的控制信息和控制计算机提供的平台姿态信息，实现平台横滚角、俯仰角、方位角的伺服控制。

软件采用模块化设计。软件开发平台使用VisualC++ 6.0，数据库使用Access数据库，矩阵运算使用自编的C++矩阵运算类。

软件分为以下几个模块：人机界面模块、系统设置模块、基本参数输入模块、数据存储/读取模块、硬件通信模块、矩阵运算模块、IMU导航计算模块、零速修正模块、初始调平和自主寻北模块及伺服控制模块。软件总体结构如图6所示。

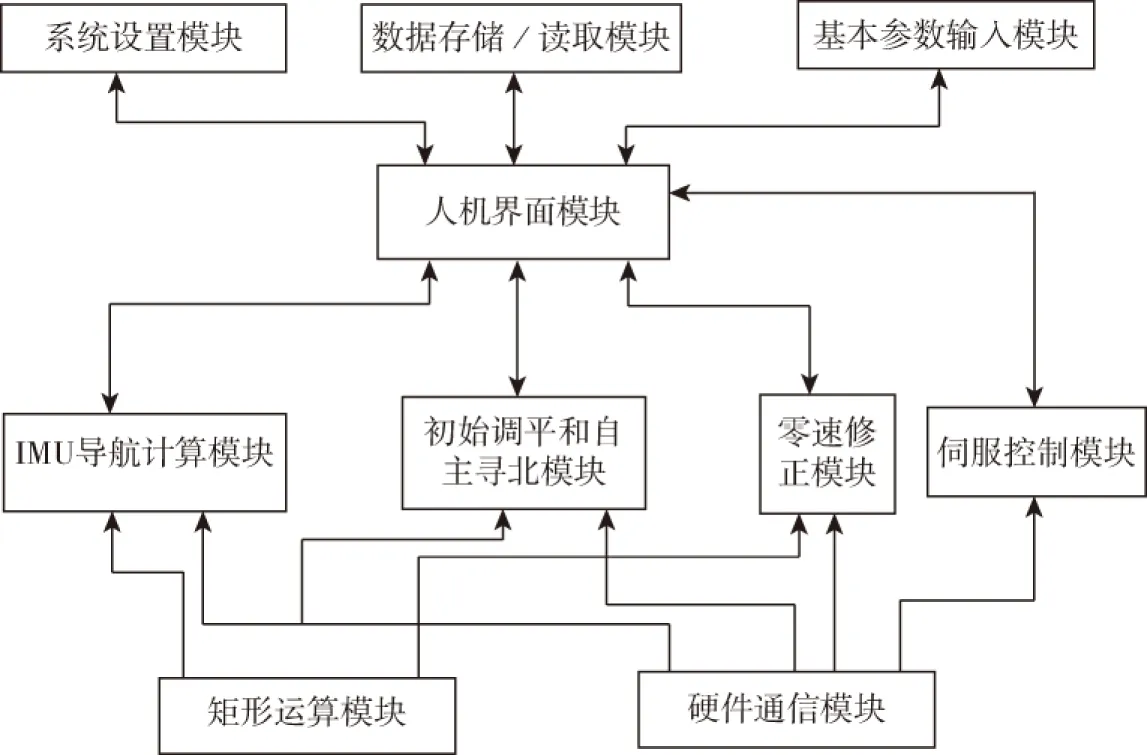
图6 软件总体结构图Fig.6 The overall structure drawing of software

3 结束语

地空导弹行进间稳定发射平台是行进间发射技术的重要组成部分，适用于导弹发射车行进中发射导弹、雷达车行进中搜索目标等领域，在军事领域中具有广阔的应用前景。

[1] 胡寿松. 自动控制原理[M].北京：科学出版社，2013.

[2] 刘超, 高双. 自动控制原理的MATLAB仿真与实践[M].北京：机械工业出版社，2015.

[3] 谢刚. 全球导航卫星系统原理：GPS、格洛纳斯和伽利略系统[M].北京：电子工业出版社，2013.

[4] 王生捷. 发射控制技术[M].北京：北理工大学出版社，2015.

[5] 胡振文. 车辆定位与导航[M].北京：中国铁道出版社，2009.

Research on a Stabilized Launch Platform on Moving Vehicle for Ground-to-Air Missile Weapon

MA Zhi-gang, LUO Gang ,YIN Kang-jun

(Military Representative Office of the People’s Liberation Army in 3655 Factory,Zunyi 563000,China)

A stabilized launch platform of ground-the-air missile weapon on the moving vehicle is studied, some technology problems, such as attitude measuring precision and dynamic level stability control of launch platform on the moving vehicle are mainly analyzed.Through the study, the stability of launch platform is improved.

Ground-to-air missile weapon;Launch platform

10.19306/j.cnki.2095-8110.2016.03.009

2015-10-08；

2016-02-18。

马志刚(1972-)，男，工程师，主要从事地空导弹发射控制技术方面的研究。

TJ761.1

A

2095-8110(2016)03-0051-07