MEMS加速度计组合在分度头上的标定方法

高 亢，陈希军，任顺清

(哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150080)

MEMS加速度计组合在分度头上的标定方法

高 亢，陈希军，任顺清

(哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150080)

提出了一种在分度头上标定MEMS加速度计组合的测试方法，该方法可以标定出加速度计组合的刻度系数误差、加速度计零偏、三轴不正交度误差、安装误差角，同时可以分离出分度头转位机构角位置误差。首先通过建立一系列坐标系，推导了重力加速度在加速度计敏感轴的分量表达式。然后采用谐波分析法给出了误差标定方程，利用最小二乘法和Kalman滤波器进行误差参数的估计，并对估计结果进行了对比分析。最后通过三次独立实验标定结果的重复性和残差验证了该方法的正确性。

MIMU组合标定；MEMS加速度计；光栅分度头；谐波分析法； Kalman滤波

0 引言

加速度误差系数的辨识多采用多位置法，根据不同的加速度计采用不同的位置取向，例如绕性加速度计采用的12点翻滚测试法，MEMS加速度计测试常采用六位置测试法。文献[1]中介绍了利用高精度三轴转台标定MEMS加速度计组合的六位置测试法，标定出了加速度计的零偏、刻度因子和安装误差。文献[2]提出利用普通气泡水平仪和六面体盒状物实现加速度计组合的六位置现场简易标定方法，但是该方法只能标定低精度的加速度计，文中标定的加速度计分辨率只有3.9mg。

在现有的文献中，有利用光栅分度头完成加速度计单表在重力场中标定的研究。文献[3]提出了一种在分度头上标定加速度计单表的全组合测试方法，该方法能够在标定加速度计误差模型的同时，处理分度头的角位置误差，从而提高了标定精度。文献[4]则是通过正交双表两种安装位置的测试方式，从加速度计的输出中分离出分度头的角位置误差。

本文提出了一种在光栅分度头上标定MEMS加速度计组合的方法，该方法可以标定出误差模型中的加速度计组合的刻度系数误差、零偏、三轴不正交度误差、安装误差角以及分度头转位机构的角位置误差。在没有精密转台的情况下，利用光栅分度头就可以得到高精度的标定结果。

1 测试系统

如图1所示，整个测试系统由光栅分度头、MEMS惯组、夹具等组成。光栅分度头相当于一个单轴转台，绕旋转轴转动的角位置分辨率为0.1″，其精度远高于MEMS加速度计的测试精度，因此其角位置误差可以忽略不计。此外，分度头还有一个俯仰轴，使分度头可以绕图1中的Y轴方向在0°～90°范围内转动。但是俯仰轴的角位置是由机械游标直接读出，角位置精度只有3′左右，因此角位置误差是不能忽略的，本文标定加速度计时需要将其考虑在内。

图1 测试装置Fig.1 Testing equipment

将旋转轴的角位置记为α，转位机构的角位置记为β。利用水平仪调整加速度计敏感轴方向与分度头坐标系方向一致，记α=0°、β=0°。实验的测试步骤如下：

1)分度头转位机构处于零位β=0°，依次转动分度头角位置为α=0°、45°、90°、135°、180°、225°、270°、315°，记录三个加速度计的输出Ax0、Ay0、Az0。

2)调整分度头转位机构使β=45°，依次转动分度头角位置为α=0°、45°、90°、135°、180°、225°、270°、315°，记录三个加速度计的输出Ax1、Ay1、Az1。

3)调整分度头转位机构使β=90°，依次转动分度头角位置为α=0°、45°、90°、135°、180°、225°、270°、315°，记录三个加速度计的输出Ax2、Ay2、Az2。

下文中将说明如何从这三组测试数据中辨识出所有的误差参数。

2 误差参数标定模型

2.1 坐标系的建立

要想得到重力加速度在三个加速度计上的分量，必须要知道从地理坐标系到加速度计敏感轴坐标系的转换关系，因此首先定义坐标系如下：

1)地理坐标系OX1Y1Z1：即为当地地理坐标系，这里定义为东北天坐标系。OX1Y1在水平面内，OX1轴指向东向，OY1轴指向北向 ，OZ1由右手定则确定。

2)分度头基准坐标系OX2Y2Z2：如图1所示，此时分度头的旋转轴处于水平位置，分度头基准坐标系的OX2轴与旋转轴轴线方向一致；OZ2轴铅垂向上；OY2轴在水平面内，方向由右手定则确定。分度头基准坐标系不会随着分度头的旋转轴和转位机构转动。定义分度头基准坐标系OX2轴与地理坐标系OX1轴的夹角为θ，即地理坐标系挠OZ1轴旋转θ角得到分度头坐标系OX2Y2Z2。

3)安装坐标系OX3Y3Z3：该坐标系与分度头固连，随着分度头的旋转轴以及转位机构一起旋转，初始位置与分度头基准坐标系重合。

4)加速度计正交坐标系OX4Y4Z4：该坐标系定义为理想的加速度计敏感轴坐标系。加速度计在夹具上的安装以及夹具在分度头上的安装都会产生安装误差角，定义加速度计正交坐标系OX4Y4Z4和安装坐标系标系OX3Y3Z3之间的误差角为[δθxδθyδθz]T，其中δθx、δθy、δθz都是小角度。

5)加速度计敏感轴坐标系OX5Y5Z5：该坐标系的三个坐标轴的方向与加速度计敏感轴方向一致。由于加速度计的敏感轴存在不正交度误差，因此该坐标系为非正交坐标系。

加速度计敏感轴坐标系OX5Y5Z5与加速度计正交坐标系OX4Y4Z4的位置关系如图2所示。定义轴OX5与OX4重合，OX5Y5与OX4Y4在一个平面内，OY5轴和OX5正交，OZ5轴由右手定则确定。定义OY5与OX5的不正交度为γ21，OZ5与OX4、OY4的不正交度分别为γ31和γ32。

图2 加速度计正交坐标系OX4Y4Z4Fig.2 Accelerometers Orthogonal coordinate system OX4Y4Z4

从地理坐标系到加速度计敏感轴坐标系的转换关系如图3所示。

图3 地理坐标系到加速度计敏感轴坐标系的转换Fig.3 Transformation from geographic coordinate system to coordinate system of the accelerometers’ sensitive axs

2.2 加速度计输出表达式

根据图3所示的坐标变换关系可以得到加速度计敏感到的比力的表达式为

(1)

只考虑加速度计的标度因子误差和零偏时，加速度计的输出为：

Axi= (1+ΔKx)[-(sinβi+cosβiΔβi)+

δθz(cosβi-sinβiΔβi)sinα-

δθy(cosβi-sinβiΔβi)cosα]+x

(cosβδθz)sinα+(-cosβiδθy)cosα

(2)

Ayi= (1+ΔKy)[(δθz-γ21)(sinβi+cosβiΔβi)+

(cosβi-sinβiΔβi)sinα+

δθx(cosβi-sinβiΔβi)cosα+y

≈(sinβiδθz-sinβiγ21+y)+

(cosβi+cosβiΔKy-sinβiΔβi)sinα+

(cosβiδθx)cosα

(3)

Azi= (1+ΔKz)[-(δθy+γ31)(sinβi+cosβiΔβi)+

(-δθx+γ32)(cosβi-sinβiΔβi)sinα+

(cosβi-sinβiΔβi)cosα]+z

(-cosβiδθx+cosβiγ32)sinα+

(cosβi+cosβiΔKz-sinβiΔβi)cosα

(4)

2.3 误差参数辨识方案

令β=0°、45°、90°，对应的角位置误差分别为Δβ0、Δβ1、Δβ2，有：

Ax0=-Δβ0+δθzsinα-δθycosα+x

Ay0=(1+ΔKy)sinα+δθxcosα+y

Az0=(-δθx+γ32)sinα+(1+ΔKz)cosα+z

(5)

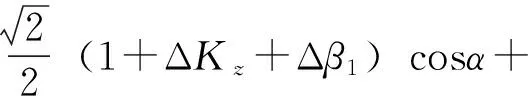
(6)

Ax2=1+ΔKx+x

Ay2=-(δθz-γ21)+Δβ2sinα+y

Az2=(δθy+γ31)+Δβ2cosα+z

(7)

为了进行误差参数的辨识，需要将式(5)、式(6)、式(7)写成如下的矩阵形式

Z=HX+V

(8)

其中，Z为观测量，X为需要辨识的误差项，H为系数矩阵，V为量测噪声。

如果直接将加速度计的输出值作为观测量，则Z为72×1矩阵，H为72×15矩阵，将使得计算量大大增加。注意到角度α是在一个周期内均匀分布的，可以将式(5)、式(6)、式(7)看成加速度计输出值的Fourier一级展开式，只要从采集的数据中分离出均值项和一次谐波系数，与表达式对应就能辨识出误差项，该方法又称为谐波分析法。

采用谐波分析法，将对应的谐波系数作为观测量，得到系统的方程为式(10)。

(9)

本文将采用最小二乘法和Kalman滤波两种方法来进行误差辨识，并对两种估计结果进行对比分析。最小二乘法的估计方程为

X=(HTH)-1HZ

(10)

需要辨识的误差状态量是不随时间变化的静态变量，因此将通用的Kalman滤波方程简化为：

(11)

其中，K为增益矩阵，P为协方差矩阵，R为量测噪声。

3 仿真分析

首先，通过Matlab仿真来验证该方案的正确性与可行性。仿真设置的误差参数为刻度系数误差ΔK=[0.0002 -0.00012 0.0003]，零偏安装误差角不正交度转位机构角位置误差为了模拟MEMS加速度计的输出,加入均值为0、标准差为0.15mg的高斯噪声作为量测噪声。

采用最小二乘法和Kalman滤波对误差参数进行估计，估计结果如图4～图8所示。可见，最小二乘估计结果中含有较大噪声，Kalman滤波可以很好地将噪声去除，误差参数的估计值大约在300组数据后收敛。

最小二乘法的估计结果中噪声太大，严重影响估计精度，因此采用滤波的方法对估计结果进行再处理，将前N次估计结果的均值作为第N次的估计值，处理结果如图9所示。

图4 标度因数估计过程Fig.4 Scale factor estimation process

图5 零偏估计过程Fig.5 Bias estimation process

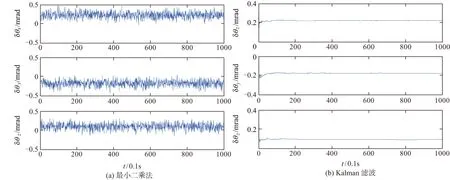
图6 安装误差角估计过程Fig.6 Installation error angle estimation process

图7 不正交度估计过程Fig.7 Non-orthogonality estimation process

图8 角位置误差估计过程Fig.8 Angular position error estimation process

将滤波处理后的最小二乘结果与Kalman滤波估计结果进行对比，仿真结束时刻两种方法给出的估计值的差值小于10-6，认为估计精度是一样高的，但是Kalman滤波的收敛速度比滤波处理后的最小二乘法要快，因此后文的测试实例中将直接采用Kalman滤波来辨识误差参数。

4 测试实例

依照测试方案分别进行了3次测试。实验时IMU的采样频率设置为125Hz，每个位置的采样时长为20min，3次实验之间IMU断电15min。表1为第一次测试的数据均值。表2为误差参数辨识结果。

表1 第一次测试数据

表2 误差系数标定结果(Kalman滤波)

4 标定结果分析

4.1 实验重复性分析

由于实际模型参数不可知，只能通过多次标定进行标定参数的重复性检验。MEMS加速度计目前还没有统一的测试标准，本文根据文献[12]中给出的的惯性级SIMU多次标定重复性指标结合本次实验测试，用MEMS加速度计的性能指标给出适用于MEMS加速度计测试的重复性指标：加速度计标度因数的相对误差为5×10-4，安装矩阵元素的绝对误差为5mrad，三轴不正交度绝对误差为2mrad，零偏的绝对误差为1.5mg。

从表2可以看出，标定结果满足重复性指标，说明该标定方法是可靠的。

4.2 残差分析

根据式(8)，残差为

V=Z-HX

(12)

三次测试的残差如表3所示。

表3 标定残差

实测数据的1s标准差为1.2mg，100s标准差为0.7mg。从表3可以看出，3次实验的标定残差最大值均为±0.5mg左右，小于加速度计的量测噪声，认为满足精度要求，说明该方法是有效可行的。

5 结论

本文主要是提出了一种在单轴光栅分度头上标定MEMS加速度计组合的测试方法，通过坐标变换得到了包含待标定误差的重力加速度在加速度计敏感轴上的分量表达式。采用谐波分析法给出了误差标定方程，相对于直接利用加速度计输出值作为观测量的方法大大减少了方程的维数，从而减少了误差辨识的计算量。分别用最小二乘法和Kalmam滤波对误差参数进行了估计，仿真结果表明Kalmam滤波相对于最小二乘法收敛速度快、稳定向好且精度高，能有效去除量测噪声影响，提高标定精度。

为了验证该方法的实用性进行了3次独立的测试实验，并对标定结果进行了分析。3次试验标定结果的重复性满足加速度计标度因数的相对误差5×10-4，安装矩阵元素的绝对误差5mrad，三轴不正交度绝对误差2mrad，零偏的绝对误差1.5mg的重复性指标；残差绝对值为0.5mg符合精度要求。该方法操作简单，标定精度高，使得不具备精密转台设备的实验室也可以标定高精度的MEMS加速度计组合，具有一定的工程实用价值。

[1] 宋丽君, 秦永元.MEMS加速度计的六位置测试法[J].测控技术, 2009, 28(7): 11-13.

[2] 彭孝东, 张铁民, 李继宇, 闫国琦.三轴数字MEMS加速度计现场标定方法[J].振动、测试与诊断, 2014, 34(3):544-548.

[3] 任顺清, 冯士伟, 马向斌.加速度计的全组合标定方法[J].中国惯性技术学报, 2007,15(6):760-764.

[4] 董春梅, 陈希军, 刘庆博, 任顺清.正交双加速度计两种安装位置在重力场中的标定方法[J].中国惯性技术学报, 2014, 22(5): 693-700.

[5] 孙枫, 曹通.基于Kalman滤波的加速度计十位置标定方法[J].系统工与电子技术, 2011, 33(10):2272-2276.

[6] Babichenko A V, Shkred V K.Main error of inertial navigation systems[J].Engineering Physics, 2011, 11(3): 34-53.

[7] 李巍, 任顺清, 赵洪波.惯性元件的失准角分离技术研究[J].哈尔滨工业大学学报, 2012, 44(1): 43-46.

[8] 陆辰, 李荣冰, 刘建业, 杭义军.微型航姿系统中三轴MEMS加速度计组合误差建模方法[J].测试技术学报, 2011, 25(1):29-34.

[9] 薛亮, 李天志, 李晓莹.基于MEMS传感器的微型姿态确定系统研究[J].传感技术学报, 2008, 21(3):457-460.

[10] 张红良, 武元新, 练军想, 吴文启.基于转台误差分析的高精度惯测组合标定编排改进[J].中国惯性技术学报, 2010, 18(1):129-134.

[11] 尹小恰.精密离心机工作半径的测试方法与误差分析[D].哈尔滨工业大学, 2013.

[12] 严恭敏, 李四海, 秦永元.惯性仪器测试与数据分析[M].北京: 国防工业出版社, 2012.

Calibration Method for MEMS Accelerometers Based on Dividing Head

GAO Kang，CHEN Xi-jun， REN Shun-qing

(Space Control and Inertial Technology Research Center, Harbin Institute of Technology,Harbin 150080,China)

This paper proposes a method for calibrating three-triad accelerometers on an indexing table.The calibrate scale factors, biases, misalignment angles of three input axes, and the pitch errors of the turntable were separated from the outputs of the accelerometers.Firstly, components of gravity in the accelerometer input axes are deduced by establishing a series of coordinate systems and propagating different attitude errors.After that, the calibration model equation is built by harmonic analysis method and the error parameters were estimated using the least square method and Kalman filter.Finally, the correctness of this method was verified by three independent experiments under the same condition.

MIMU calibration;MEMS accelerometer;Indexing turntable;Harmonic analysis method;Kalman filter

10.19306/j.cnki.2095-8110.2016.03.012

2015-12-19；

2016-01-05。

国家重大科学仪器设备开发专项(2013YQ310737)

高亢(1991-)，女，在读博士，主要从事捷联惯导初始对准方面的研究。E-mail：condi_gk@163.com

V441

A

2095-8110(2016)03-0074-010