基于滑坡监测数据的时间序列位移预测

蔡泽宏，简文彬,3，李宏达，罗阳华

(1.福州大学 环境与资源学院， 福建 福州 350108；

2.福州大学 岩土工程与工程地质研究所， 福建 福州 350108;

3.福建省地质灾害重点实验室， 福建 福州 350002)



基于滑坡监测数据的时间序列位移预测

蔡泽宏1,2，简文彬1,2,3，李宏达1,2，罗阳华1,2

(1.福州大学 环境与资源学院， 福建 福州 350108；

2.福州大学 岩土工程与工程地质研究所， 福建 福州 350108;

3.福建省地质灾害重点实验室， 福建 福州 350002)

摘要：滑坡位移变形的产生及演变，对于滑坡安全稳定性的评价至关重要。以德化县美湖乡上际村桥亭头滑坡为例，将边坡失稳时的总位移分解成位移的趋势项和位移的周期项，通过时间序列方法对滑坡位移进行预测，在监测数据的模糊离散性与随机性的基础上以及变形参数所呈现的相关规律，通过GM(1，1)的灰色模型获得位移的趋势项，采用了时间序列的方法对其进行拟合，并通过自回归(AR)模型使得非平缓时序转化为平缓时序。最终再通过时间序列加法得到滑坡总位移预测值。结果显示具有较高精度，对了解边坡位移的发展趋势以及研究边坡的动态稳定性是有效可行的。

关键词：变形监测；时间序列；灰色模型

滑坡位移未来预测一直成为众多学者研究防治滑坡灾害的重要手段，而它的分析方法也从原来的监测点的位移-历时曲线到后来的主要通过数学模型对位移-历时的统计数据进行分析，定性分析滑坡位移的动态趋势变化[1]。另外研究边坡失稳的主要影响因素权重及作用方式，找出滑坡位移变化与其影响因素之间的关系[2]。

伴随着概率统计、灰色理论、神经网络模型以及模糊数学等各类数学方法的产生和应用，在20世纪80年代后给滑坡未来位移预测提供了方法与理论基础[3]。目前较流行的滑坡预测理论多建立于位移监测数据上进行分析，通过相关的数学模型进行拟合。但是在边坡失稳变形过程中会受各种因素的影响，如降雨强度、爆破情况、地下水水位变化、水文地质条件等等。一些学者提出了时间序列方法，利用非平稳的时间关系，从而建立出一套有效反映出影响因素与滑坡位移变化规律的动态预测模型，此类方法得到了极大的推广[4]。

1模型详述

1.1实例介绍

该滑坡地处于半山腰凹坡处，场地原始斜坡高程750 m～810 m，相对高差60 m，自然坡度约28°，边坡整体呈凹形坡，原为水田，滑坡发生后改为旱地。上部残坡积层黏性土，灰黄色、硬塑，结构松散，厚约5 m，边坡下部基底为强风化粉砂岩(T1X)。而汇水面积60 000 m2，地下水主要为第四系残坡积孔隙潜水，坡脚出露多处泉水。目前该滑坡体处于不稳定的状态。

1.2数据预处理

由于野外监测数据是离散的(本文的位移监测数据时间间隔约为6 h)，并且遇到特殊情况(天气恶劣或其它原因导致的数据不能传回)，监测数据出现间断，这对于位移数据的分析和对滑坡位移的预测是非常不利，因此在进行滑坡位移预测前需要对其进行预处理[5]。

滑坡位移预处理步骤如下：

(1) 滑坡位移数据的等间距化和顺序化

监测数据中部分数据出现没有按照时间数据进行排序的情况，这可能是由于监测软件的部分错误或设置导致的，因此按照时间由早到晚进行排序，时间按照时间顺序进行排列。

为了将不等间距的滑坡位移数据进行等间距化，首先设定起始时间，本文的监测数据起始时间为2009-12-25 17∶07，结束时间为2010-09-16 8∶01，因此将起始时间设置为0时刻，每隔6个小时(360 min)判断该时刻在监测数据中所处的位置，即前后时刻及位移数据，利用线性插值法获取每隔6小时时刻的位移数据，这样就形成了间距为6小时的位移数据，方便进行数据的处理和分析。

(2) 滑坡位移数据的去噪

对于滑坡位移数据，虽然其噪声不高，但由于其主要由监测仪器自动监测完成，不可避免存在一些噪声，对未来的滑坡位移预测造成一定的误差，阈值去噪方法是我们在小波分析中的常用的去噪方法。在小波的变换过程中可具有一些特性及优点：

① 系数的分布区间较为分散，而在信号改变后小波的熵会下降，具有低熵性的特点;

② 有效反映信号改变中的非平稳特性，如小波的边缘、尖峰以及断点等具有多分辨率特性;

③ 在小波产生改变后的噪声出现了白化的现象，此类方法在实际中得到大量推广，比传统的时域去噪方法效果更好，具有去相关性;

④ 由于在小波变换中确定出基函数不受约束，故能根据其小波特性及去噪特性来确定小波，选取具有基函数灵活性。

很多学者提出小波变换的方式来进行小波信号去噪。通过对小波分解后的模(各层的系数)介于系数的一定阈值间进行分别处理，然后对成功处理的小波系数再进行一次反变换，获得的新信号此时已经成功去噪。这种通过阈值去噪方法是一种实现起来相对简单的小波去噪方法，也被广泛应用于工程实际。

具体步骤为：

① 位移数据的小波分解，本文采用Daubechies5阶分解方法；

② 小波分解高频系数的阈值量化，采用VisuShrink方法[6](或称统一阈值值处理)；

在小波重构时，一般采用将高频系数进行阀值量化获直接使用已分解的低频系数，在利用处理后的高频系数和已分解的低频系数来重新建立出滑坡位移数据的小波。

1.3时间序列分解

对于滑坡产生的位移而言，可以看做是一个随时间变化的时间序列。通过利用时间序列的分解方法建立出关于滑坡位移预测预报模型，以动态监测滑坡的位移变化。一般来说，时间序列{yt}可直接或简介利用函数变换后分解成多项相加的形式，具体如下式：

yt=Tt+St+Ct+It

(1)

式中: yt是时间序列中总位移；Tt是位移的趋势项，表示出在长期的滑坡演化过程中时间序列变化的位移趋势；St是位移的季节项，表示出在实际监测中的位移数据随时间变化而呈现出的季节性的波动；Ct是位移的循环周期项，反映出了在时间序列中的非季节的循环周期变动波动；It是位移的随机项，反映出在时间序列中的随机因素的作用，并且也可看出各种因素对于时间序列产生的影响。本文中把位移的季节项和循环周期项合并为周期项,能够有效反映出由位移的季节变化与周期变化具有较强的一致性，以及时间序列总的周期变化。由于随机项对滑坡演化中位移变化的作用带有不可确定性，本文在此暂不作考虑。

1.4数学模型的建立

当边坡出现失稳时，通过时间序列理论，可将其位移变化看做是一个在时间变化中单调增长。然而它的变化发展并不平缓，同时在滑坡演化中位移变化还受到多方面的影响：坡体自身位移发展演化；外界诱发的因素的综合作用[7]。坡体自身地质条件对位移趋势项的控制以及受到降雨、地下水水位变化同地质条件变化等因素影响位移的周期项都是其主要原因。在此，本文将时间序列的数学模型可概括为下述形式：

X(t)=φ(t)+η(t)

(2)

其中：X(t)为总位移的时间序列；φ(t)为位移的趋势项函数；η(t)为位移的周期项函数。

在时间序列方法中，确定位移趋势项，通常使用的是二次移动平均法，以消除时间序列总位移中在时间周期的影响因素；另一方面，可通过灰色模型来获得位移的趋势项，之后再通过其位移与历时的时间变化关系进行拟合。以时间序列加法数学模型为基础，可以在滑坡监测的总位移中筛分出位移的趋势项以获得位移的周期项。位移的周期项是一个非线性时间序列，同时受到多个因素共同影响。因自回归(AR)模型能够有效的对位移的周期项分量进行预测。最终得到的总位移预测值则是位移趋势项数值与位移周期项数值总加[8]。

对于滑坡演化过程中，自重势能和外界因素综合控制影响了坡体的位移变化。对此，在德化县美湖乡上际村桥亭头滑坡位移时间序列分析过程中，即可认为其滑坡的总位移数值是位移趋势项值与位移周期项值的相加之和。

(1) 对位移趋势项的各部分分离及预测

本文采用二次移动平均法来对位移趋势项的各部分进行分离，其中滑坡位移长期趋势变动代表着坡体未来位移的变化规律，其计算方法如下：

将监测数据观测值的时间序列记为yt(t=1，2，…，N)，则其中前两次位移的平均值可记作Mt(1)，Mt(2)，故有

(3)

位移的趋势项具有极大不确定因素，受多种因素的影响，前文提到的位移周期项，具有循环周期的特点，在这里取周期项式中n=6，其中一次位移则大约需要半个周期。故所得的二次位移的平均值Mt(2)即为总位移的趋势项值。在不断动态变化过程中的灰色系统也随之产生。滑坡位移时间序列可分解为：

x(0)={x(0)(1)，x(0)(2)，x(0)(3)…x(0)(n)}

(4)

经累加后将上式处理后可得出累加数列：

x(1)={x(1)(1)，x(1)(2)，x(1)(3)…x(1)(n)}

(5)

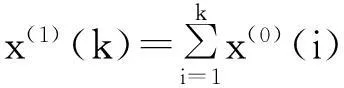
(6)

其中：a,μ为未知的参数值。

如果x代表滑坡的位移，那么式(6)中的微分方程的解为:

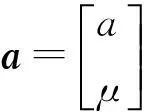
a=(BTB)-1BTYN

(7)

其中B大小为(n-1)×2，YN大小为(n-1)×2，n为位移数据长度，具体为

(8)

(9)

(2) 周期项分离及预测

在位移的周期项获取中，利用在原始位移序列中筛分出位移的趋势项，并通过利用时间序列的数学模型来得出。yt(t=1，2，…，N)来表示这随机过程中的为时间序列，在这里，t指当前所处的时刻。而在数学模型构建中，在随机过程中，总位移的时间序列在筛分出位移的趋势项后的其它部分则可视为稳定的的序列来求解。在建立AR(p)自回归模型后，则自回归方程为：

xt=β1xt-1+β2xt-2+…+βpxt-p+at=

(10)

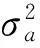
(11)

可依据如下步骤进行

① 模型阶数上限值设定为nk，阈值区间取

N/3≤nk≤N/2；

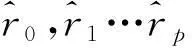
(12)

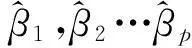
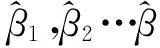
在AR(p)模型定阶、代入之前获取的位移的周期项，估计自回归参数等计算值后，将滑坡位移周期项获得值与位移的预测值进行对比，以此验证出时间序列方法求取滑坡未来位移的有效性。

通过时间序列加法模型X(t)=φ(t)+η(t)，经由模型计算预测得到的趋势项位移值与周期项位移值相加，即可得到总位移预测值。

2预测结果对比分析

2.1滤波前后对比

如图1所示，通过对比可以看出，通过滤波和等距化处理之后，滑坡体在中部深度7m处的位移值更加连续和光滑，体现了位移值的变化规律，且没有失去位移的变化规律，为后面需要建立的趋势项和周期项位移预测模型建立重要的数据基础。

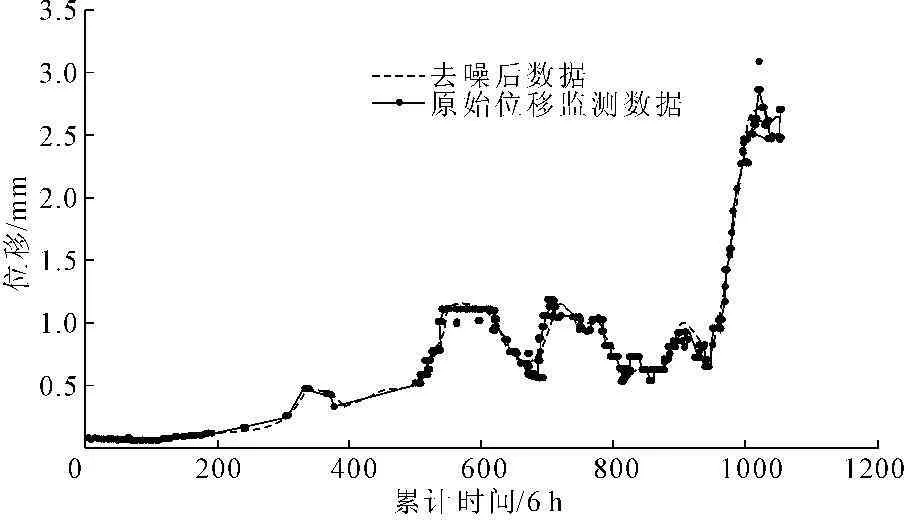
2009-12-25 17∶07～2010-09-16 8∶01

图1深部7m处位移滤波前后对比图

2.2趋势项位移与周期项位移预测

从图2可以看出，趋势项位移主要代表滑坡体位移的趋势值，以递增为主，趋势项位移的预测值与实际值存在一定的误差，这主要是由于滑坡体的位移受强降雨，地下水位上升下降变化，土体强度变化等条件下，坡体位移出现周期性或随机性的变化所造成的[9]，因此属于周期预测值的范围；在周期项位移值的分析中，我们可以看到周期项位移以波动性和周期性变化为主，而本文利用AR(p)模型对其进行拟合和预测，可以较好的预测滑坡体的位移[10]。

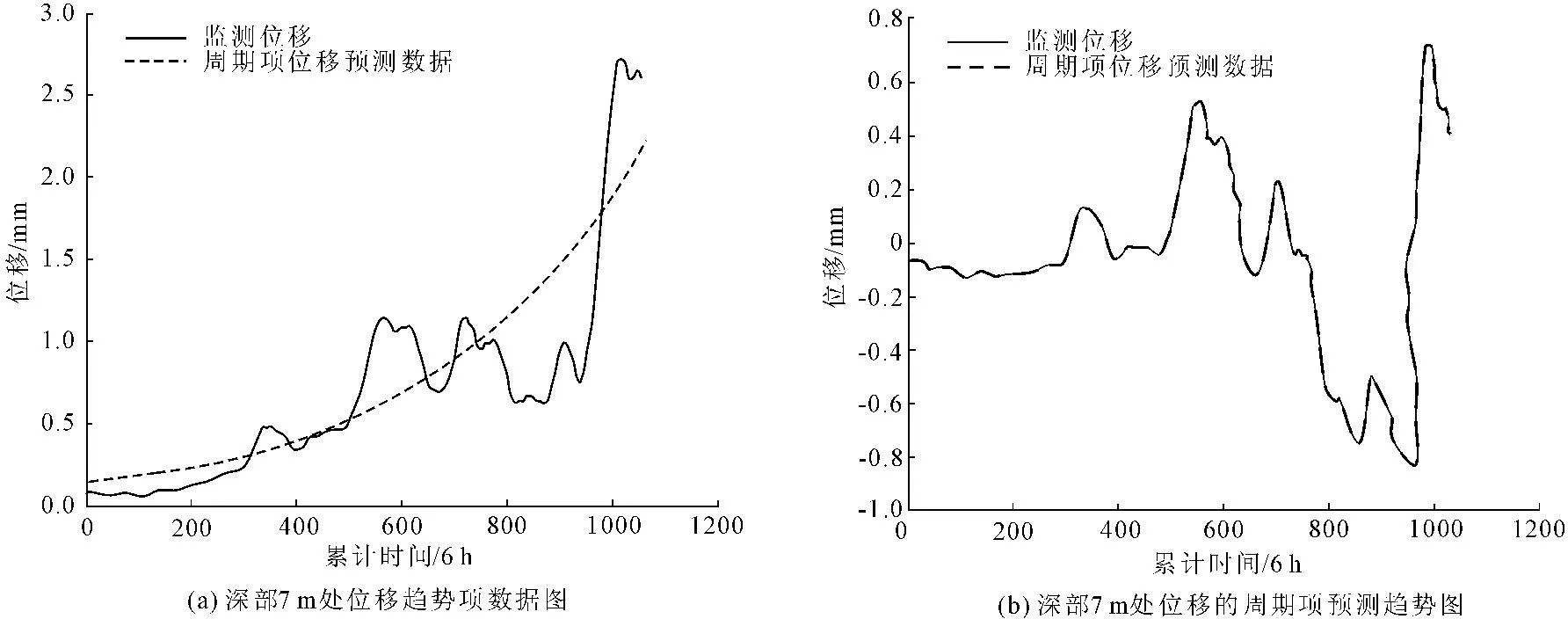
图2深部位移变化趋势图

2.3未来位移预测

将位移的趋势项和位移的周期项相加，可获得出滑坡整体位移值，并可以对其进行迭代预测。通过图3可以看到，利用本文基于时间序列的数值算法可以很好的拟合滑体位移变化趋势，并预测滑坡体的位移。

根据已有的判断经验分析，可以得到基于监测数据的位移预测模型分析，其精度大大提高的原因在于删除了之前的老信息数据，而这种陈旧信息对预测的作用可能是有害无益的。所以，滑坡灾害时间预测时，数据越新，预测效果也就越好，随着数据的增多，陈旧信息应逐渐被删除，以建立新陈代谢模型[11]。

2.4不同位置位移综合分析

为了对德化县美湖乡上际村桥亭头滑坡的位移进行综合分析，为了我们对所有的监测数据进行综合，尽量获取立体的位移数据特征。由图4可以看出，深部位移数据的监测，在一个钻孔中(钻孔编号QTZK-6)，深度分别为7m和9m，钻孔地表坐标约为(180m，770m)，坐标系与图4相同，x轴代表距离坡脚距离，y轴代表其标高。地表位移分为上部和下部，其中上部坐标约为(320m，805m)，下部坐标为(220m，775m),其中下部地表位移监测点与深部位移监测点距离坡脚位移较近。

图3　深部7 m处整体位移预测图

图4位移数据监测位置示意图

通过地质勘查资料可知，滑面位置位于Qdl第四系坡积层、砂质黏土与T1X三叠系下统溪口组地层的交界面处，T1X三叠系下统溪口组地层主要为强风化粉砂岩和粉砂质硅泥岩，灰色，散体状，原岩结构可辨，含原岩碎块，而上部第四系坡积层和黏土层为软塑—硬塑状态，强度较低，因此在交界处已发生相对滑动。

通过对比四个位置监测位移数据，可以发现以下几个特征：

(1) 地表位移特征

通过图5可以看出，上部和下部表层累计位移均为波动式增加方式变化为主，其中滑坡体上部表层位移变化明显，最大可达190mm，下部表层位移最大值约为28mm，这说明滑坡体在2009年—2010年内以上部的推移破坏，拉裂上部坡体为主，上部的坡体在潜在滑面处不断的产生应力集中，通过本文基于时间序列的滑坡位移预测可以发现，上部表层位移通过较大的变形后开始出现稳定，而下部表层位移则继续增大，这也说明对与滑坡体，上部已出现稳定，而下部则会出现继续滑移破坏的趋势。

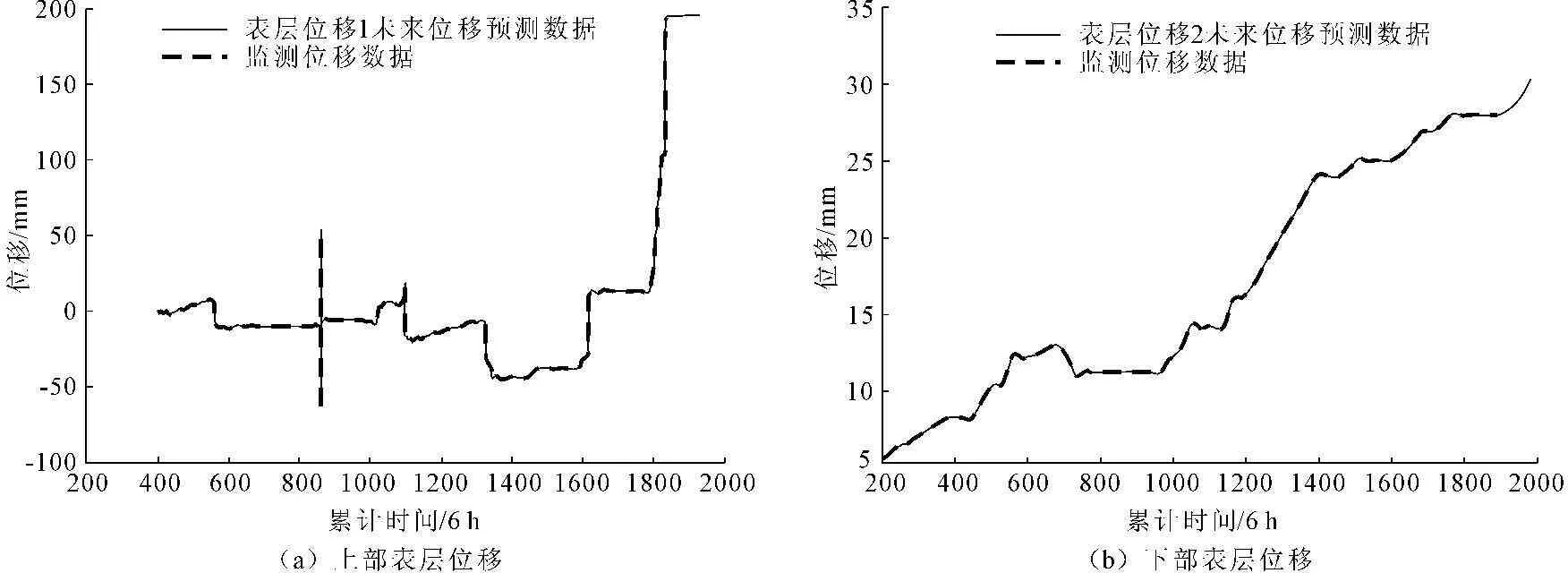
图5表层监测点位移及预测值

(2) 深部位移特征

对于整个滑坡体来说，深部位移监测点位于中部的位置，如图6所示，在已监测的数据中，7m处位移最大值达到2.5mm，9m处位移最大值达到10mm，可以看出下部位移较上部位移大约7.5mm，均比表层位移变化小，这说明虽然中上部经历了滑坡体位移较大的变化，但中下部则对滑坡体位移的继续发展起到阻止作用，并且表层和底部的位移大于中部的位移，这说明对于滑坡体，不同地层，不同部位出现不同的变形特征，这与滑坡体不同部位土体物理特性，强度特征有重要关系。

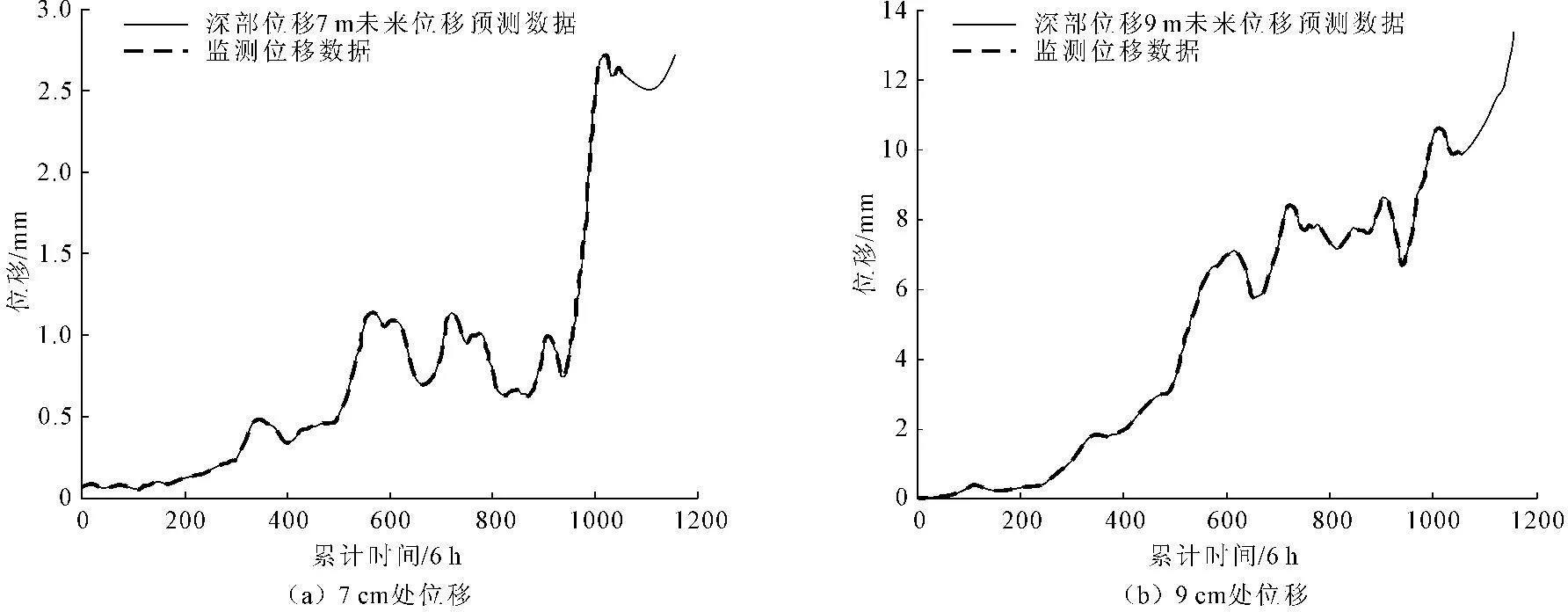
图6深层监测点位移及预测值

对于实例滑坡体位移的预测分析，我们可以看到，对于7m处，其位移在峰值2.5mm处波动变化，说明该地层范围内土层基本处于稳定，但易受到降雨作用，地下水位升降等外界因素的影响而发生波动变化。而9m处位移在未来则会继续增大，这与该区域范围内表层位移变化趋势基本一致，这说明该监测点附近位移表层和深层(9m处)会继续增大，滑坡处于不断加剧破坏状态，亟需进行防治。

(3) 综合特征

通过对比上下四个监测点的位移可以发现，滑坡体以上部滑移破坏为主，从而推动中下部的滑坡体位移不断增加，且上部位移最大达到190mm，基本处于稳定状态，应力不断集中；中下部位移较小，最大表层位移为30mm左右。中下部位移又以上层和下层(9m)变化幅度最大，而中层(7m)的变化幅度最小，其出现的差异说明中下部位移受地层特性、地下水位变化等因素的作用明显。

3结语

通过对德化县美湖乡上际村桥亭头滑坡位移监测数据进行详细的分析，根据数据的特点建立了基于时间序列的滑坡位移预测模型，对滑坡体不同监测点的位移进行了分析和预测，得到了如下结论：

(1) 基于实际的位移监测数据，需要进行数据预处理，时间序列的分离和数学模型的建立三个步骤，才可以对滑坡体的监测数据进行分析和预测。

(2) 在对监测数据进行预处理时考虑了数据模糊离散性和缺失性，并根据监测数据动态变化，对原有的陈旧数据进行重新筛分、剔除，变形滚动地进行预测位移。从而对真实的反映出实际滑坡位移时动态变化的情况。

(3) 基于时间序列的滑坡位移数学模型将位移分为趋势项和周期项，可以较好的拟合现有位移数据，并且对未来滑坡位移具有较好的预测功能。

(4) 利用改进后的数学模型改进了灰色模型的不足，并有效结合了GM(1，1)灰色模型和时间序列方法二者的优势，最终得到滑坡位移预测曲线与实际监测数学模型获得位移-历时的曲线一致程度较高，对边坡未来位移的预测预报工作具有重要意义。

(5) 通过对比现有滑坡位移数据和滑坡位移的预测值，可以发现滑坡的可能破坏面位置，在本文实例中，桥亭头滑坡以上部滑移破坏为主，且已趋向稳定，下一阶段将转变为中下部的滑坡体滑面贯通，位移加速破坏阶段，整体为欠稳定状态。

参考文献：

[1]徐峰，汪洋，杜娟，等.基于时间序列分析的滑坡位移预测模型研究[J].岩石力学与工程学报，2011，30(4):746-751.

[2]蒋刚，林鲁生，刘祖德，等．边坡变形的灰色预测模型[J]．岩土力学，2000，2l(3)：244-246．

[3]刘华夏，张献州．基于时间序列分析的地铁变形监测数据建模与预报研究[J]．铁路勘察，2010,35(6)：17-19.

[4]杨叔子，吴雅，轩建平．等．时间系列分析的工程应用(2版)[M].武汉：华中科技大学出版社，2007：1-19．

[5]郝小员，郝小红，熊红梅,等．滑坡时间预报的非平稳时间序列方法研究[J]．工程地质学报，1999，7(3)：279-283．

[6]张东明．陈江，何洪甫，等．动态修正时距权重的不等时距灰色模型及应用[J]．岩土工程学报，2012，34(6)：1137-1141．

[7]GuzzettiF,PeruccacciS,RossiM,etal.Therainfallintensity—durationcontrolofshallowlandslidesanddebrisflows：anupdate[J]．Landslides，2008，5(1)：3-17．

[8]靳奉祥，王同孝，独知行．变形观测中的模式识别问题[J]．中国有色金属学报，1997，7(3)：18-21．

[9]魏迎奇，孙玉莲．大坝沉降变形的灰色预测分析研究[J]．中国水利水电科学研究院学报，2010，8(1)：25-29．

[10]刘大杰，陶本藻．实用测量数据处理方法[M]．北京：测绘出版社，2003：72-99．

[11]彭令，牛瑞卿．三峡库区白家包滑坡变形特征与影响因素分析[J]．中国地质灾害与防治学报，2012，22(4)：1-7.

Displacement Prediction by Using Time Series Analysis Method Based on the Monitoring Data

CAI Zehong1,2, JIAN Wenbin1,2,3, LI Hongda1,2, LUO Yanghua1,2

(1.CollegeofEnvironmentandResources,FuzhouUniversity,Fuzhou,Fujian350108,China;2.InstituteofGeotechnicalEngineeringandEngineeringGeology,FuzhouUniversity,Fuzhou,Fujian350108,China;3.FujianKeyLaboratoryofGeohazardPrevention,Fuzhou,Fujian350002,China)

Abstract：The generation and evolution of landslide displacement are very important to the evaluation of the stability of slope. In this paper the landslide displacement was separated into trend term and periodic terms which were analyzed and predicted by using time series analysis method. Take the Qiaotingtou landslide which happens at Shangji village bridge in Dehua county as an example, after analyzing the fuzzy discrete and stochastic properties of the monitoring data, the GM(1,1) model was adopted to predict the trend term, and auto regression model was adopted to transform the non-stable time series into stable time series, which were put back together to derive the total value of landslide displacement. The results show that it is fairly accurate and could be used predict landslide displacement and evaluate the stability of slope.

Keywords:deformation measurement；time series；grey model

文章编号：1672—1144(2016)01—0236—07

中图分类号：P642.22

文献标识码：A

作者简介：蔡泽宏(1990—)，男，福建福州人，硕士，研究方向为地质灾害防治。E-mail:wanqiuyuheiqiu1@qq.com通讯作者：简文彬(1965—)，男，福建永定人，教授，博导，主要从事地质灾害防治、工法创新研究。E-mail:jwb@fzu.edu.cn

基金项目：国土资源部地质灾害防治重点实验室开放基金资助项目(NO.FJKLGP2012K001)；福建省自然科学基金(2015J01164)

收稿日期：2015-09-19修稿日期：2015-10-18

DOI:10.3969/j.issn.1672-1144.2016.01.045