任意采样频率转换滤波器的设计与实现*

何健标

(深圳职业技术学院电信学院通信系　深圳　518055)



任意采样频率转换滤波器的设计与实现*

何健标

(深圳职业技术学院电信学院通信系深圳518055)

摘要提出了一种可以实现任意数字信号采样频率转换的数字内插滤波器设计方法。论文从转换滤波器的频域响应要求出发，设计等波纹内整数插滤波器作为原型，通过原型滤波器的时域插值和卷积得到任意采样频率转换滤波器。原型滤波器和时域插值滤波器可以精确控制采样频率转换滤波器的频率响应，是理想滤波器的最佳一致逼近，在各种相同响应时间的滤波器中性能最优。

关键词任意频率转换; 数字内插; 等波纹奈奎斯特滤波器; Sinc滤波器

Design and Implementation of Interpolation Filter for Arbitrary Sampling Rate Conversion

HE Jianbiao

(Department of Communication, Shenzhen Polytechnic, Shenzhen518055)

AbstractA method is presented to implement arbitrary digital signal sampling rate conversion filter. According to design requirement of frequency response, this method uses equiripple nyquist filter as prototype filter, and is obtained by time-domain interpolation and convolution. The prototype filter and time-domain interpolation filter endow the ability to accurately control its frequency response under various circumstances. And the arbitrary sampling rate conversion filter provides not only the best performance among all kinds of filters with the same response time, but also the best Chebyshev approximation of ideal filter.

Key Wordsarbitrary sampling rate conversion, digital interpolation, equiripple nyquist filter, Sinc filter

Class NumberTP391

1引言

在数字信号处理中不同采样率的信号处理模块需要进行信号采样频率转换，任意频率转换可以通过数字内插滤波器实现，该数字滤波器模拟实现信号的重采样过程，在此过程中需要抑制原信号频率以及谐波上的镜像。

任意采样频率转换滤波器的实现基本都采用Fallow结构[1]、Gardner和Vesma分别采用多项式[2~3]和多分段函数[4]来逼近理想滤波器的时域冲激响应。由于时域冲激响应的截断，上述方法都无法控制滤波器实际频响和理想滤波器频响的最大误差。为获得对理想频响的最佳一致逼近，采用穷举搜索的方法寻找使得滤波器频响最大误差最小化的最佳系数[5]，但是在滤波器的系数较多或是精度要求较高时，穷举搜索耗时过长并不适用。宫丰奎等[6]在文献[4]的基础上推导出一组经验系数可以无需搜索而得到性能较好的滤波器，但如果该滤波器无法满足设计要求，文献[6]并没有提出进一步改善滤波器性能的方法。本文跳出从时域逼近理想滤波器的传统思路，以可实现的等波纹奈奎斯特FIR滤波器为原型，通过时域插值和时域卷积获得任意采样频率转换滤波器的时域冲激响应，该滤波器具有频率响应精确可控的优点，可根据设计要求灵活调整参数以适应各种不同的应用场合。

2模型

内插滤波器的信号处理过程如图1：输入信号X(i)的采样率为1/TI，经过内插滤波器后输出信号Y(n)的采样率变为1/TO。传统的模拟信号处理过程是先将输入序列X(i)经过数模转换变成模拟信号，再通过模拟滤波器的内插虑除信号的镜像，最后经过频率为1/TO的二次采样得到输出信号Y(n)。为了在数字域更好地模拟上述过程实现采样率的转变，内插滤波器应该和模拟滤波器一样希望具有更大的阻带衰减，更小的通带纹波和符号间串扰。

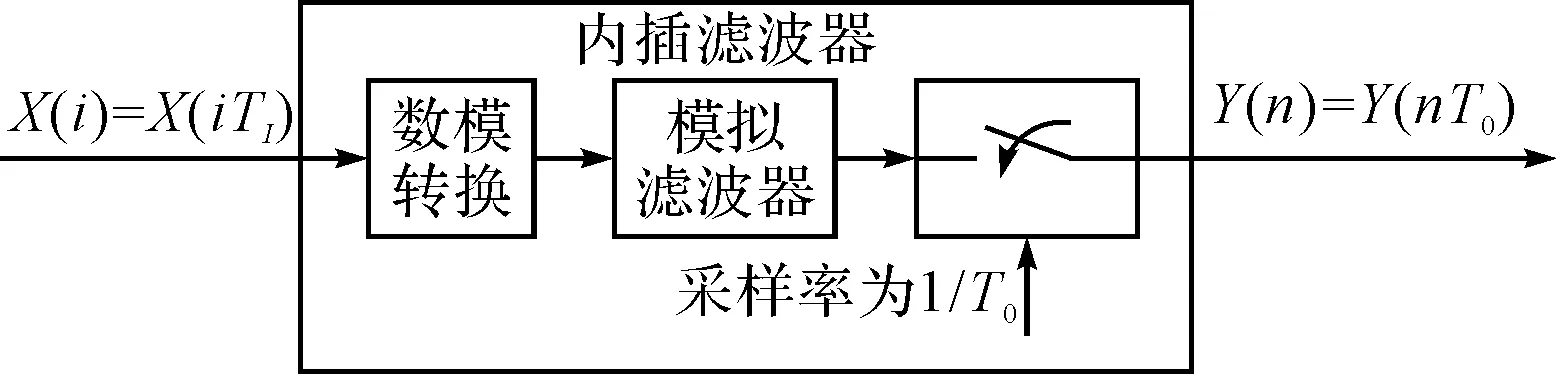
图1　内插滤波器的等效模型

内插滤波器的设计要求如下：对于码元周期为TI的输入序列X(i)设计一个阻带衰减不低于γdB，通带纹波不大于δp的无符号串扰滤波器h(t)，使信号通过该滤波器后输出序列Y(n)的采样率变为1/TO，即：

Y(n)=Y(nTO)=∫X(τ)×h(nTO-τ)dτ

(1)

3算法

任意采样频率转换滤波器与传统内插滤波器最大的不同在于采用性能出色的FIR滤波器作为原型滤波器。

原型滤波器对输入序列而言是一个N(奇数)阶线性相位FIR插值滤波器，其内插因子为M，响应时间为L·TI，为便于电路实现规定M和L必须为2的正整数幂，则：

(2)

为避免原型滤波器产生符号间的干扰，应采用半带或是升余弦等奈奎斯特滤波器；若要使原型滤波器的抽头最少，等波纹滤波器是最佳选择[7]，Samueli对奈奎斯特滤波器的特性进行了详细分析[8]。根据分析信号带宽B，通带纹波δp和阻带衰减γ(dB)的等波纹Nyquist滤波器设计过程如下：

令L=2，计算通带截止频率ωp，阻带频率ωs和阻带纹波δs

(3)

N阶(N=L·M+1)线性相位Nyquist滤波器其频率响应为

(4)

其中Z为所有M的倍数的集合[8]。设计等波纹Nyquist滤波器就是求解(M-1)L/2个非零系数an，使得H1(ejω)是对理想滤波器频率响应的最佳一致逼近。

等波纹滤波器至少应该有ML/2+1个频率极值点[7]，而H1(ejω)在阻带内至少有(M-1)L/2个频率极值点[8]，由此可得到(M-1)L/2个线性方程，再采用Remez交换算法[7]可以推导出(M-1)L/2个极值点，并进一步求解出an和δ1

如果δ1≤δs，则H1(ejω)是等波纹滤波器的频响，h1(t)=IDFT[H1(ejω)]是其时域冲激响应；如果δ1≥δs，将L增大一倍(L=L·2)重新计算滤波器频率响应，直到重新计算的δ1满足δ1≤δs为止。

等波纹Nyquist滤波器在设计中只对阻带作等波纹逼近，可精确控制阻带纹波；对于通带纹波则根据Nyquist滤波器的频响经过周期延拓是一直线的特点，具有以下约束关系：

δpass≤(M-1)δstop

(5)

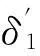
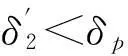
设计时域插值FIR滤波器H3(ejω)(图3(c))。H3(ejω)也是一个等波纹Nyquist滤波器，其内插因子M3=M/M2，该滤波器对应的阶数是N3=L·M3+1，其频率响应的阻带频率是ωs=2π·M2÷M-ωp，根据Remez交换算法[7]可以推导出(M3-1)L/2个极值点，并进一步求解出H3(ejω)。

原型滤波器H2(ejω)和时域插值滤波器H3(ejω)级联得到经过时域插值调整的原型滤波器H4(ejω)，即：

(6)

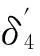
Sinc滤波器的时域冲激响应是一矩形脉冲，可用于抑制H4(ejω)的镜像频率。定义一个矩形脉冲的门函数g(t)作为Sinc滤波器的时域冲激响应，其闸门宽度为TI/M：

g(t)=ε(-TI/2M)-ε(TI/2M)

(7)

其中ε(t)为阶跃函数。矩形脉冲经过傅立叶变换为Sinc函数，呈低通特性，图3(d)中虚线就是G(ejω)的频率响应。而最佳内插滤波器的时域冲激响应h(t)(图2(d))和频率响应H(ejω)(图3(d))定义如下：

(8)

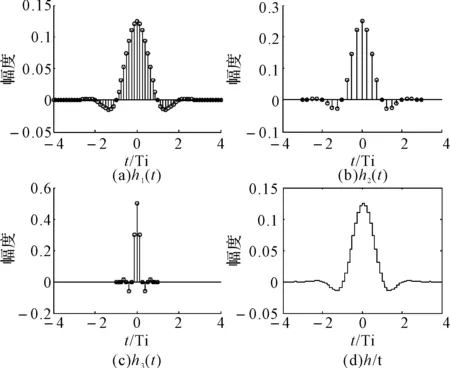
图2　时域冲激响应

影响任意采样频率转换滤波器性能的主要是通带纹波和阻带衰减。通带纹波衡量滤波器对有用信号的扭曲程度，阻带衰减衡量滤波器的对无用信号的抑制能力。

滤波器阻带分为两部分：一是对应于H4(ejω)阻带的衰减δFIR，一是H4(ejω)的各个镜像的衰减δlmage。在H4(ejω)的阻带内，若H4(ejω)自身阻带衰减为δ4，Sinc函数对应的衰减是δSinc，则δFIR=δ4×δSinc。由于设计原型滤波器已保证了δ4小于设计要求的阻带衰减，加上δSinc的衰减，因此δFIR肯定满足设计要求的阻带衰减。

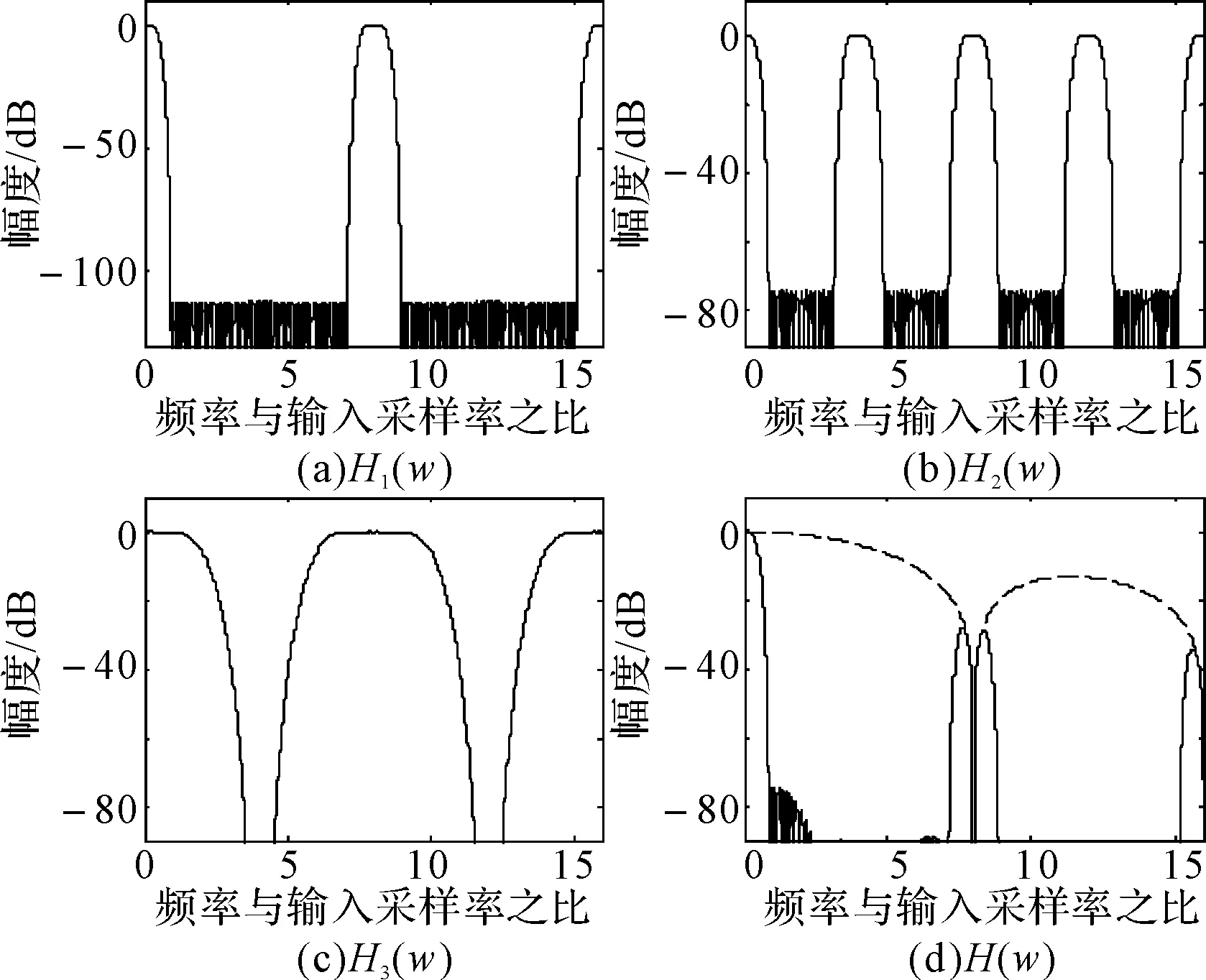
图3　频域响应

而δlmage取决于Sinc滤波器对第一镜像频点的衰减，Sinc滤波器的抑制能力取决于h4(t)采样频率(M/TI)与信号带宽B之比：其比值越大对虚像的抑制能力就越强。例如图3(d)中滤波器对数字镜像的衰减δlmage约30dB，绝大多数场合下无法满足要求，为改善δlmage，可以调整原型滤波器的内插因子M，使M/(BTI)满足衰减设计需求。

与阻带衰减相似，通带纹波由H4(ejω)的通带纹波δ4和Sinc函数的衰减决定，而Sinc函数的衰减由M/(BTI)决定。与镜像抑制不同的是，Sinc函数对通带的影响微乎其微，可以忽略；如遇到性能要求非常高的场合，根据阻带衰减得到M后，可计算Sinc滤波器对δ4的影响，在设计原型滤波器的时候予以考虑。

4实现

Fallow结构是最为经典的内插滤波器实现结构[1]，文献[6]利用系数的对称性在Fallow结构的基础上作了改进。但Fallow结构假定系统时钟等于输出采样率，这种假设随着微电子技术的高速发展明显过于保守，文献[9]提出了一种以高速乘法累加器为核心的FIR滤波器结构，通过逻辑设计中时间-空间的互换，以最优的资源消耗来实现各种性能的FIR滤波器。任意采样频率转换滤波器的实现可借鉴这种时空权衡的设计思想，以高速乘法器在TO内作多次乘法运算以实现逻辑资源的优化。

令nTO=(ik+μ)TI，其中0≤μ<1，根据式(1)，Y(n)可以写成：

Y(nTO)=

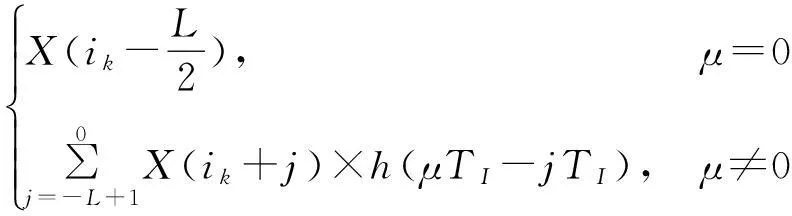
(9)

显然Y(n)的计算过程是一卷积运算，需要L次乘法和加法运算，图4是采用单个乘法累加器完成滤波所有乘加运算的实现结构：输入数据序列X(i)依次存于数据缓存中，启动信号开启计数器通过计数跳转将式(9)中计算所需的L个数据(通过数据选择器Mux)和滤波器系数(预存于ROM中)依次送入乘法累加器，L个时钟后滤波器的当前输出Y(n)计算完毕。如果L较大或是输出采样率较高，单个乘法累加器无法在TO内完成L次乘加运算，需要多个乘法累加器协同工作，参考文献[9]中MAC级联结构对图4略作修改即可。

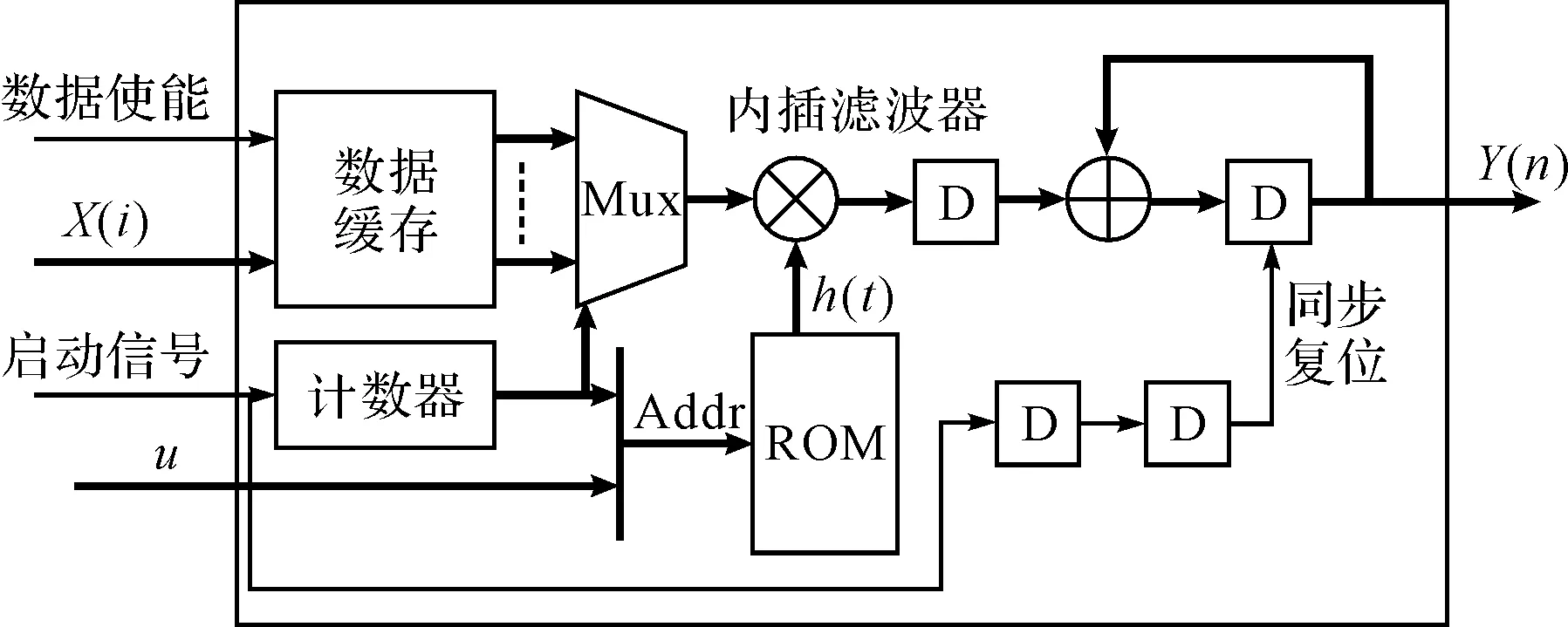
图4　最佳内插滤波器的实现结构

虽然h(t)是连续时间函数(图2(d))，但它是由h4(t)和时域闸门函数卷积而成，所以h(t)仅需保存h4(t)的系数共N个。h4(t)对于TI是无符号间串扰的VB，零系数有L个，非零系数为N-L。根据式(9)，当μ=0时，只需X(ik-L/2)即可计算Y(n)；当μ≠0时，根据μ的取值不同非零系数被分为M-1组，每组有L个非零系数参与计算当前的输出Y(n)。因此根据μ可将h(t)的系数分为M组，每组L个系数(μ=0时以零系数补足)分别存入图4的ROM中，μ作为地址指针指向各组系数的首地址，计数器作为组内偏移地址依次将该组系数逐个读出送往乘法累加器。

内插滤波器的关键参数μ在每次计算滤波器输出时都需要更新，令μ(nTO)记做μn，根据式(9)，有：

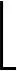
(10)

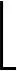
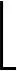
(11)

图5是μn的计算实现，其中nCO采用步进为CO的累加计数器来计算，通过常数除法器除以CI得到，最后将nCO/CI的整数部分直接丢弃得到μ。

图5μ的计算实现

5结语

本文提出了一种设计任意采样频率转换滤波器的方法，该设计以FIR滤波器为原型，频率响应精确可控，是各种应用场合通用的数字内插滤波器设计方法，尤其适用于需要高性能滤波的场合。

参 考 文 献

[1] C. W. Farrow. A continuously variable digital delay element[C]//Proc. IEEE Int. Symp. Circuits & Syst Espoo, Finland: IEEE,1988.

[2] F. M. Gardner. Interpolation in digital modems. I. Fundamentals[J]. IEEE Transactions on Communications,1993,41:501-507.

[3] L. Erup, F. M. Gardner, R. A. Harris. Interpolation in digital modems. Ⅱ. Implementation and performance[J]. IEEE Transactions on Communications,1993,41:998-1008.

[4] J. Vesma, T. Saramaki. Interpolation Filters with Arbitrary Frequency Response for All-Digital Receivers. Symp Circuits & Syst Atlanta, GA: IEEE,1996.

[5] D. Kim, M. J. Narasimha, D. C. COx. Design of Optimal Interpolation Filter for Symbol Timing Recovery[J]. IEEE Transactions on Communications,1997,45:877-884.

[6] 宫丰奎,李兵兵,张乔乔.一种利用曲线拟合设计内插滤波器的新方法[J].通信学报,2004,25:118-124.

GONG Fengkui, LI Bingbing, ZHANG Qiaoqiao. A new method for the design of interpolation filter using polynomial fit[J]. Journal of Communication,2004,25:118-124.

[7] J. H. MCCLELLAN, T. W. PARKS, L. R. RABINER. A computer program for designing optimum FIR linear phase digital filters[J]. IEEE Transactions on Audio and Electroacoustics,1973,AU-21:506-526.

[8] H. SAMUELI. On the Design of Optimal Equiripple FIR Digital Filters for Data Transmission Applications[J]. IEEE Transations on Circuits and Systems,1988,34:1542-1546.

[9] 何健标,王宏远,郭跃,等.一种基于FPGA的FIR滤波器实现结构[J].微电子学与计算机,2008,25:47-50.

HE Jianbiao, WANG Hongyuan, GUO Yue. A Novel Architecture of FIR Filter Based on FPGA[J]. Microelectronics & Computer,2008,25:47-50.

中图分类号TP391

DOI:10.3969/j.issn.1672-9722.2016.02.039

作者简介:何健标，男，博士，工程师，研究方向:通信与信息系统以及数字信号处理。

基金项目:“深圳市公共文化数字工程实验室(深圳市重点实验室)”、“南山区移动互联技术公共服务平台”资助。

*收稿日期:2015年8月11日,修回日期:2015年9月20日