基于Lyapunov的客车稳定域估计

晏愈光 许洪国 刘宏飞

摘要：针对平面稳定域在评价车辆稳定性方面的不足，提出了客车空间稳定域的一种估计方法.建立了包含Pacejka轮胎魔术公式的客车三自由度非线性动力学模型，通过仿真和实车试验对比验证了所建模型的有效性.基于客车非线性动力学模型，构建了系统Jacobian矩阵，应用霍尔维茨（Hurwitz）判据分析了车辆系统稳定性随前轮转角变化情况以及车辆的临界状态.在构建客车系统二次型能量函数的基础上，利用Lyapunov法和车辆系统稳定特性确定了客车空间稳定域.客车在满载条件下的蛇形试验结果表明：应用上述方法确定的客车行驶稳定域能够较好地表征车辆系统稳定性，可为客车操纵稳定性评价和控制提供有益参考.

关键词：客车；稳定性；3DOF非线性车辆模型；Lyapunov方法；能量函数；稳定域

中图分类号：U461.6 文献标识码：A

文章编号：1674-2974（2016）02-0015-07

当前国内外针对车辆操纵稳定性评价的行驶稳定域分析已开展了广泛的研究.国内外主要利用简化的车辆动力学模型，对车辆系统平面稳定域进行分析和探讨[1].20世纪90年代， Samsundar和Stotsky等利用Lyapunov稳定性定理和简化三次项轮胎模型得到了转向动力学系统稳定区域的解析表达式，并用数值仿真得到了系统保守平面椭圆型稳定边界[2-3].2002年，Ko和Lee基于二自由度车辆模型，利用拓扑理论确定了不同速度和前轮转角输入时，车辆系统的相平面和稳定域[4].2007年，施树明等基于势能函数曲面分析法对二自由度车辆系统稳定域进行估计，揭示了转向车辆失稳的机理[5].2013年，王睿等利用横向载荷转移率对客车阶跃转向条件下的侧倾稳定性进行研究，为车轮侧倾稳定域提供了借鉴和参考[6].

尽管相关成果对于车辆系统稳定域研究起到了推动作用，但仍存在较大的局限性.首先，稳定域分析主要基于二自由度车辆模型，未考虑多参量稳定域问题；其次，二自由度车辆模型主要应用简化的非线性三次项轮胎公式，与实际轮胎力相差较大，显著地影响系统稳定域求解的准确性；此外，分析方法对稳定域边界约束条件的确定依据不足，从而不合理地扩大了初始条件设定的范围，导致估计的稳定域与实际相差较大.

本文基于Pacejca轮胎魔术公式建立了改进的车辆非线性动力学模型，利用Lyapunov稳定理论和系统能量分析法，对双轴客车行驶空间稳定域进行分析.这对于准确分析车辆系统稳定域及评价客车操纵稳定性具有较大意义.

1非线性动力学客车模型

1.1车辆微分方程

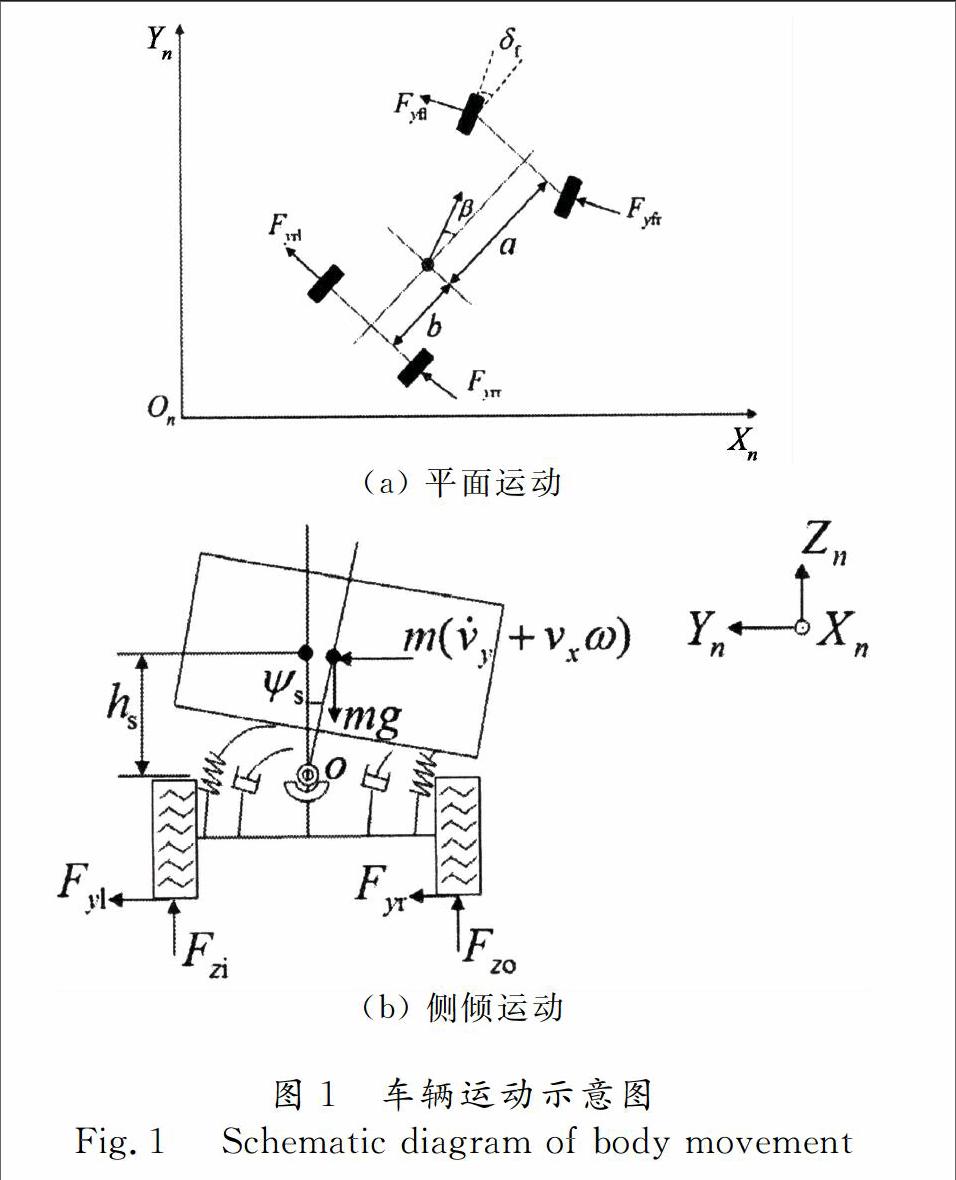
根据车辆的运动特点，对动力学车辆模型进行简化.设车辆在无制动力和驱动力状态下转向行驶，忽略车辆纵向和俯仰运动以及载荷转移变化等因素，由此构建包含客车横向运动、横摆运动和侧倾运动3个自由度的二轮模型.车辆平面和侧倾运动如图1所示.模型参数符号见表1.

2客车横向稳定性测试及模型验证

2.1车辆横向稳定性测试系统

客车横向稳定性测试系统如图2所示.测试系统主要包括汽车操舵力角测量仪HCZ-1， 双天线GPS运动参数测量仪RLVB20SL， 三轴角速度与加速度陀螺仪IMU02，以及模拟信号采集器RLVB-ADC03，此外还包括笔记本电脑和电源等.该测试系统可测量相关运动学变量，如转向盘转角、车辆行驶速度、加速度、横摆角速度、侧倾角以及制动距离、时间等.

2.2试验数据处理

试验采集的数据主要利用VBOX Tools和Matlab软件进行处理.考虑到实际测量过程中设备安装位置与车辆质心位置的偏差，测试完成后要对采样数据进行后期处理.

2.2.1IMU02陀螺仪测量参数校正

IMU02陀螺仪的坐标系定义如图3所示，箭头指向代表测试参量的正向.

由于地面坐标系和车辆坐标系均采用右手定则，因此需根据右手定则对陀螺仪采集数据进行正负坐标变换，见表3.

2.2.2质心位置状态参数确定

由于RLVB20SL测量仪的主天线和陀螺仪未置于车辆质心，为了获得车辆质心的状态参数，就要根据试验车辆上RLVB20SL测试仪的主天线和陀螺仪的安装位置及车辆状态参量间的相互关系对测试数据进行坐标转换.

2.3动力学模型验证

通过测量客车在干燥水泥路面（μ=0.70）上的运动特性与仿真结果对比，以验证三自由度车辆模型的可信性.试验车辆实行状态及测试系统布置如图4所示.

依据ISO 3888-1-1999《轿车急剧变换车道试验程序》，车辆（满载）以约90 km/h进行双移线行驶时，行驶速度和转向盘转角输入及仿真与实车试验得到的车辆侧向加速度对比情况分别如图5所示.

与实车试验结果相比，依据三自由度动力学模型仿真得到的车辆侧向加速度曲线在变化趋势和变化范围方面都具有较好的一致性，误差在10%以内，因此可认为车辆动力学模型是可信的，可为下一步研究提供依据.

图6中箭头所指方向为系统Jacobian矩阵特征根4实部随前轮转角变化方向.由图可见，当前轮转角较小时，系统Jacobian矩阵特征根实部均为负值，特征根3和4虚部为0；随着前轮转角的增大，各特征根有向原点靠近的趋势；当前轮转角约为0.042 rad时，特征根4为0，此时系统处于稳定形式改变的临界状态.这说明根据Hurwitz判据，通过车辆系统特征值能够准确地掌握系统状态，系统由稳定向失稳的转变是一个规律性的变化过程，由此可确定车辆系统稳态临界值.

4客车空间稳定域估计

由上述分析可知，当车辆以一定速度转向行驶时，系统Jacobian矩阵特征根是体现系统稳定性的重要方面.传统的基于相平面的稳定域分析没有全面考虑系统稳定性特性，从而不合理地扩大了初始条件设定的范围，导致求得的稳定域与实际相差较大.因此，在分析车辆系统稳定性的基础上，本文基于Lyapunov法结合车辆系统稳定特性估计客车空间行驶稳定域.