创业板与主板的波动溢出效应与市场风险度量研究：基于FGARCH-M-VaR模型※

马杰

（北京航空航天大学，北京 100083）

创业板与主板的波动溢出效应与市场风险度量研究：基于FGARCH-M-VaR模型※

马杰

（北京航空航天大学，北京 100083）

文章采用FGARCH-M模型研究了创业板与主板的收益波动溢出效应，并用VaR模型度量了二者的市场风险。研究意外发现，尽管创业板与主板的收益之间互有溢出效应，但二种效应却不尽相同，主板对创业板的波动溢出效应并不存在；而且，创业板与主板的条件波动率都不存在有"杠杆效应"，这可能与我国股市暴跌时通常有政策护盘有关。研究表明，VaR模型可较好度量创业板与主板的市场风险，平均来说，创业板市场风险远高于主板，风险溢出率约在40%以上。

创业板；主板；GARCH类模型；风险价值

一、引言与文献回顾

2009年10月30日，首批28家创业型公司在深交所正式挂牌，标志着我国初步形成了以主板、中小板和创业板为主体的多层次资本市场体系。与主板市场主要接纳已成熟的、规模足够大的企业不同，创业板上市的成长型企业具有成立时间较短、经营规模较小、业绩并不突出、上市门槛较低等特点，故创业板市场风险通常高于主板。实际上，我国创业板市场自推出以来，其股价波动幅度明显高于主板，呈现的暴涨暴跌对主板市场产生着深刻影响。故分析创业板市场与主板市场的相互影响，并度量二者的市场风险加以比较，对完善我国多层次的资本市场建设具有重要意义。

自Engle(1982)提出ARCH模型以来，GARCH类模型得到了长足发展，常用子模型包括GARCH (Bollerslev,1986)、EGARCH(Nelson,1991)、PARCH (Ding etal.,1993)、TARCH(Zakoian,1994)。结合风险价值VaR度量，Diamandis等(2011)采用偏斜t分布，分别测算了发达国家/东南亚/拉美国家的股票指数风险，发现一天向前的VaR测算结果、对多头与空头头寸均有明显改善。Stavroyiannis等(2012)利用Pearson-IV型分布来改进GARCH模型中对新息过程分布的描述，发现其基于VaR风险的刻画能力要优于偏斜t分布。张金林、贺根庆(2012)利用多变量时变条件相关DCC-GARCH模型与向量自回归VAR模型，探析了创业板和主板的时变联动及波动溢出效应。耿庆峰、黄志刚(2013)运用VaR模型测度了创业板市场风险，发现不同股指收益分布假定下计算的VaR值差别不大。郭乃幸等(2013)从收益性和流动性两方面，研究了主板和创业板市场之间的溢出效应。郑平(2014)采用GARCH类模型对沪深300指数的模拟估算，发现与现实指数的损益率相比，模型成功率较高。任继勤等 (2015)基于GARCH-VAR方法，比较分析了主板与创业板的市场风险，认为二者存在显著差异。

在国内外学者研究的基础上，本文首先运用FGARCH-M模型研究了创业板与主板的收益与波动溢出效应；再以度量的条件波动率为基础，运用VaR模型比较了创业板与主板的市场风险，得到了一些意外发现。

二、样本方案说明与统计特性分析

创业板指数的正式编制与发布，始于2010.6.1日。为比较创业板与主板的溢出效应与市场风险，本文以创业板指数与沪深300指数分别为创业板与主板的度量标的①；样本区间选为2010.6.1～2016.3.31，除去节假日共包括1416个有效样本点，数据来源于Wind数据库。本文的样本统计特性分析、FGARCH-M建模与VaR风险度量，均利用Eviews9. 0软件实现计算。

以股价指数收盘价为基础，可计算其百分数对数收益率rt：

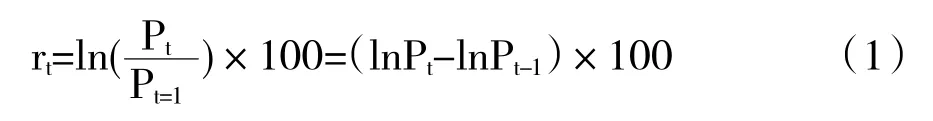
其中，Pt与Pt-1分别为第t与第t-1日的股指收盘价。

（一）描述性统计与正态性检验

首先将按公式（1）处理好的股指收益率序列，进行描述性统计，结果如表1所示（保留小数点后四位，括号内为检验统计量的P-Value值）。

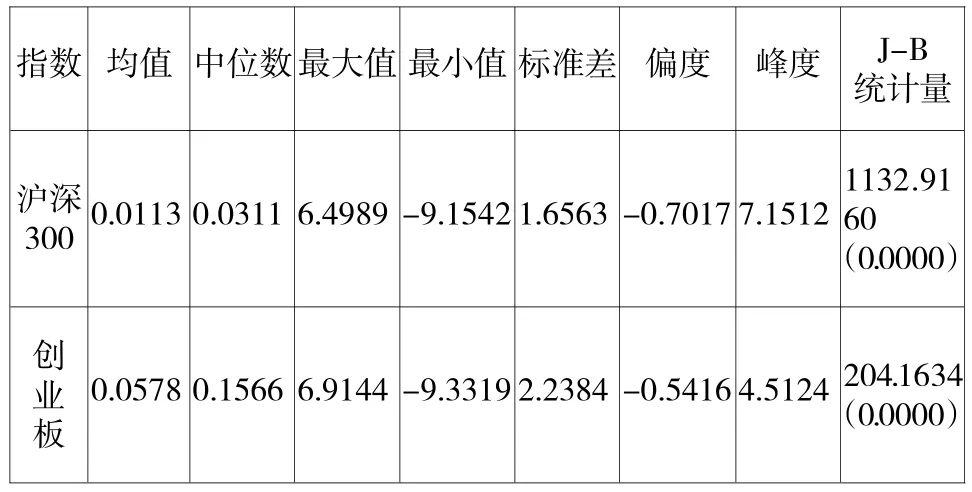
表1 沪深300与创业板指数收益率序列的描述性统计

表1显示，无论是以均值还是以中位数度量，创业板收益要明显高于主板，体现了投资创业板更好的财富效应；但同时，创业板的极差与标准差，也要高于主板，波动性更大。沪深300与创业板指收益的偏度均小于0，说明二者分布均存在左偏，即负收益时的左尾拖得更长；再从峰度系数均远大于3来看，表明二者都呈现明显的"尖峰厚尾"现象。J-B统计量的P值均接近于0，说明沪深300与创业板指收益不服从正态分布，这可从下图1的Q-Q图中进一步得到佐证。

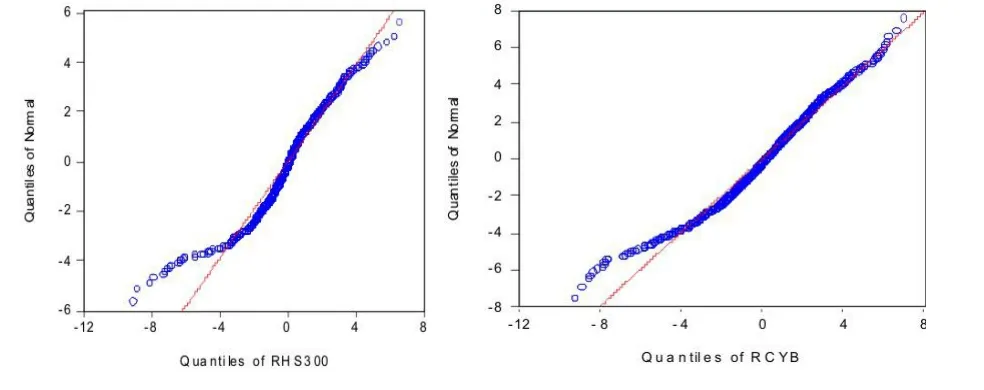
图1 ：沪深300与创业板指数收益的正态分位数Q-Q图

（二）平稳性检验

本文选择ADF方法检验了收益率序列的平稳性，结果如表2显示：两者的τ统计量值，均小于各自在1%、5%、10%标准下的ADF检验临界值；由此可知，RHS300序列和RCYB序列都是平稳的。

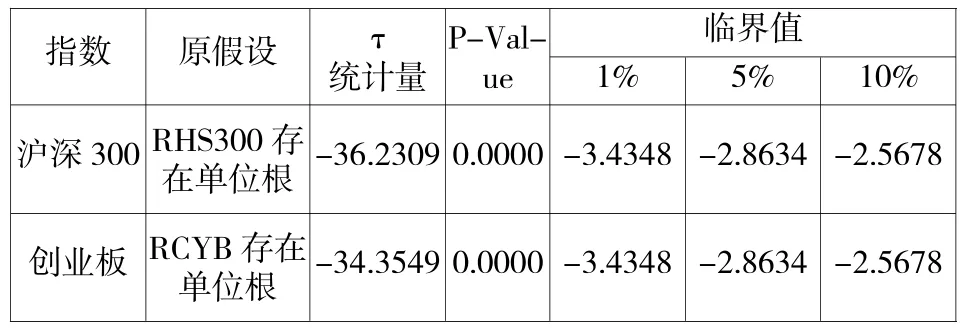
表2 沪深300与创业板指数收益率序列的ADF检验

（三）相关性与异方差检验

依据自相关ACF系数、偏自相关PACF系数及其相应滞后阶数的Q统计量②，可知沪深300与创业板指收益率均存在较为严重的序列相关；再从ARCH效应检验的LM统计量结果来看，二者也都存在着严重的ARCH异方差效应。

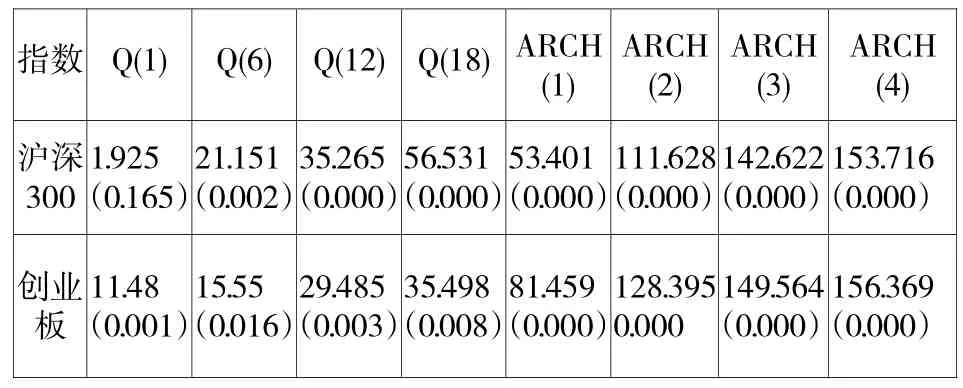
表3 沪深300与创业板指数收益率序列的自相关与ARCH效应检验

综合样本数据的统计特性分析结果，沪深300与创业板指收益序列不适用于多元线性回归模型，较适用于采用GARCH类模型来建模。

三、基于FGARCH-M模型的创业板与主板溢出效应研究

（一）FGARCH类模型简介

一般GARCH(m,s)模型，可描述为：

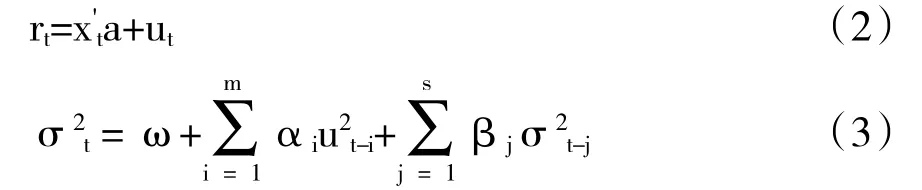
其中，rt为股指对数收益率，xt为相关解释向量，ut为均值方程残差，σ2t为ut的条件方差。一般情况下，GARCH(m,s)模型阶数并不需要很高，GARCH(1, 1)可很好地拟合异方差的问题。

此外，金融理论表明，具有较高风险的资产可获得更高的平均收益。在GARCH类模型中，利用条件方差来表示预期风险的模型，被称为ARCH-in-Mean或ARCH-M模型。它把条件方差影响、引进到均值方程中，同时亦允许条件方差受外生变量影响：

其中，f(σ2t)为基于条件方差度量的预期风险函数，通常可采用σ2t、σt与log(σ2t)三种形式；波动率方程中的vt，是影响条件方差的外生向量。

为刻画条件方差对资本市场正/负冲击的非对称效应，Glosten etal.(1993)及Zakoian(1994)提出了门限GARCH(threshold GARCH,TGARCH)，其波动率方程为：

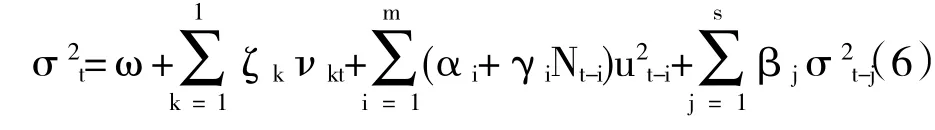
其中，示性函数N取值为：

与此类似，Nelson(1991)提出了指数EGARCH模型(exponential GARCH)，Ding et al.(1993)提出了幂PARCH模型(power ARCH)，等。Hentschel(1995)提出了一个模型，变换其参数可得到各种GARCH子模型，称之为FGARCH类模型（即Family GARCH）。

（二）创业板与主板FGARCH-M建模的实证结果

根据前文统计特性分析，主板与创业板指收益率均不服从正态分布。因此，本文分别采用残差服从广义误差分布下的基本GARCH(1,1)、仅考虑收益溢出的GARCH(1,1)-M、考虑收益波动溢出的GARCH (1,1)-M、考虑收益波动溢出的TGARCH(1,1)-M模型，对创业板与主板指数的收益波动溢出效应、进行建模分析，结果如表4、表5所示。

由表4可知，均值方程中引入RHS300收益溢出与预期风险σt，可将模型解释效力"由模型1的0.0073、提高为模型2的0.4564"，这说明：1、主板RHS300指数收益率，对创业板指收益率有明显影响，回归系数高达0.985；2、创业板指收益率也受其条件波动率的影响，条件标准差每提高1个单位、股指收益率将上升约0.24%。表4的模型3与模型4显示，创业板条件方差，不受主板指数收益变动的影响；同时，也不存在有非对称正负冲击效应，即创业板指波动性对市场下跌的反应、并没有明显超过对市场上升的反应--这个有趣的发现，与我们的直觉不太相同。

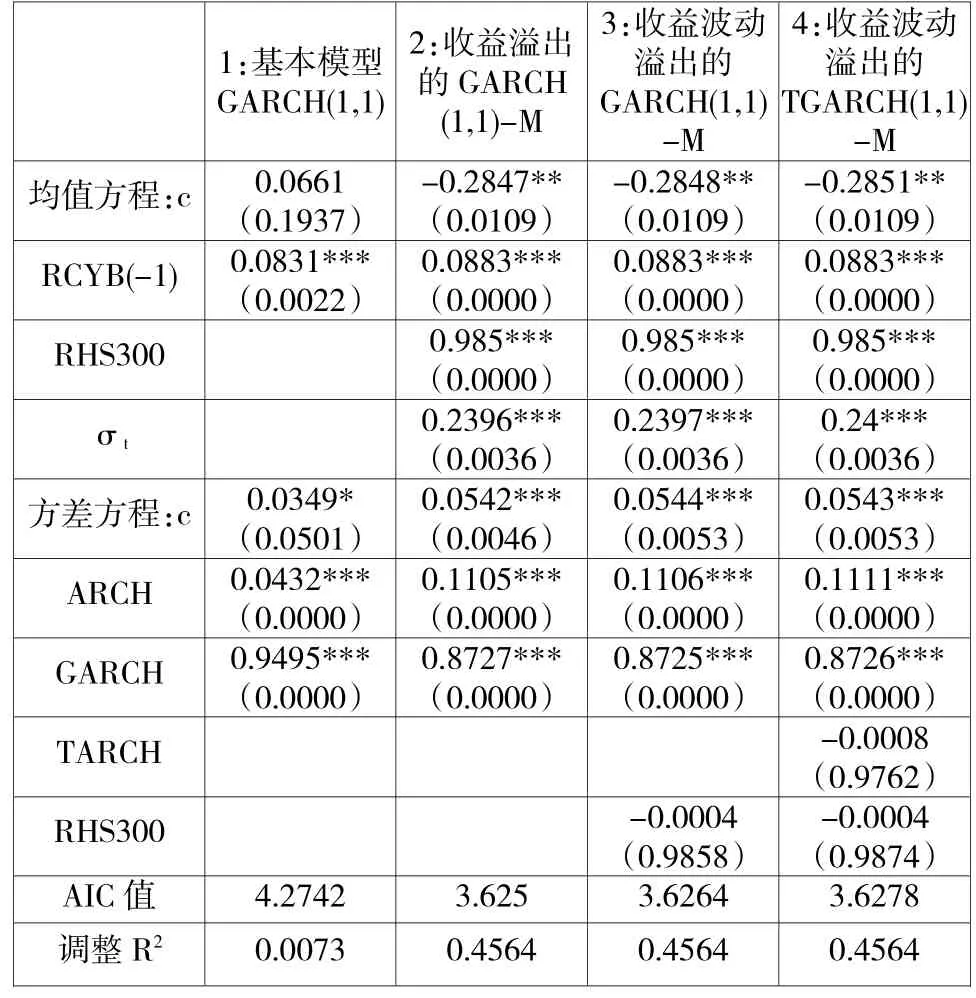
表4 创业板指数收益率的FGARCH-M建模

表5结果显示，主板RHS300的波动性对其股指收益并没有显著的解释效力，这与创业板指的情况完全不同。而且，虽然创业板波动性不受主板收益变动的影响，但主板波动性却确实创业板收益变动的影响；且创业板的正收益有助于降低主板波动性，这说明当有限资金流向创业板时、主板的资金运作力度将有所下降。当然，与创业板指实证结果类似的也有两点：1、创业板指数收益率，对主板RHS300收益率亦有明显影响，创业板指每涨1%、将拉动主板指数提高约0.5%；2、与创业板指情况类似，主板条件波动率也不存在有“杠杆效应”，这可能是中国股市特有的政策护盘导致的。

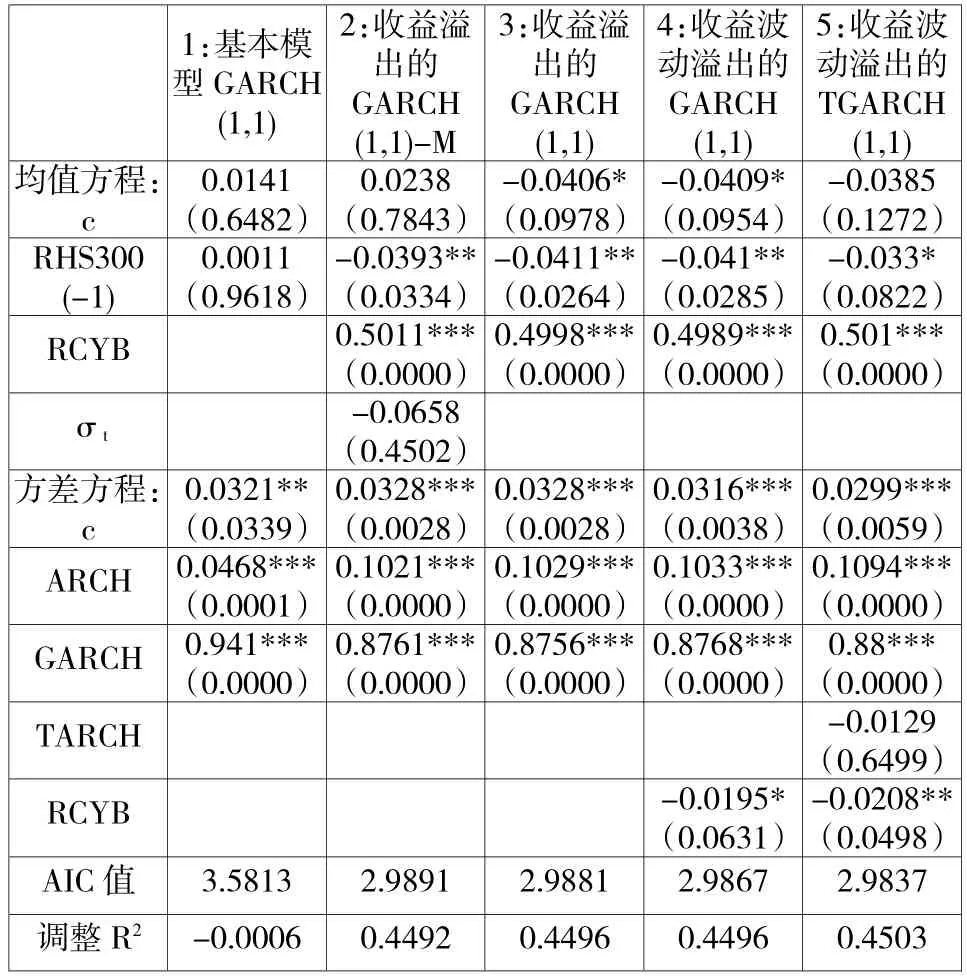
表5 沪深300指数收益率的FGARCH-M建模

以上所有GARCH模型的残差经过LM检验，均不再存在有序列相关性；同时考察表4、表5的主要变量，不同模型回归系数差异较小，显示估计结果具有较强稳健性。为进一步检验实证结果的稳健性，采用EARCH、PARCH等其他GARCH类模型，及将残差设置为t分布，所得结果、均与上表中报告的类似；限于篇幅，此处省略了这些实证结果。

四、创业板与主板的市场风险度量：基于VaR模型

风险价值VaR（Value atRisk），是指在一定时间间隔与置信水平下，其标的资产组合所面临的最大风险损失。McNeiletal(2005)将VaR定义为最小分位数：

其中，l为损失，F(l)为损失分布。

VaR计算方法，包括参数法、历史模拟法与Monte-Carlo法。大样本情况下，若资产组合收益率可近似看成是正态分布时，可由下式计算VaR：

其中，Zα为标准正态分布分位数；σt为标的资产条件波动率，Δt为风险度量的时间间隔。基于以上GARCH类建模，分别利用表4中的模型2与表5中的模型4、可估计创业板与主板的条件波动率；再利用公式（9），可估算出创业板与主板市场风险的VaR度量，结果如图2、图3所示。

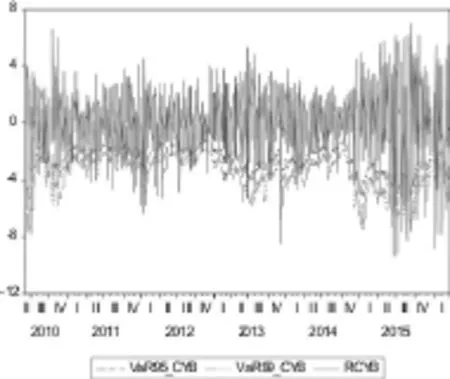
图2 ：创业板实际收益率与VaR度量

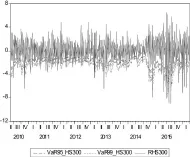
图3 ：主板实际收益率与VaR度量

由图2、图3可知，创业板与主板的实际收益率（实线）基本都在VaR风险值（虚线，报告了95%与 99%置信水平下的两种VaR）的上方，即实际损失没有超过VaR。换句话说，在绝大多数情况下，VaR度量较好的反映了创业板与主板指数的市场风险。

在VaR风险度量基础上，还需对其准确性检验，通常采用Kupiec失败检验法。假定实际损失，低于VaR为成功、超过VaR为失败：若VaR度量有效，则模拟失败率应小于等于预先设定的显著水平α；反之亦然。本文计算了GED分布下VaR估计结果的描述性统计，并采用失败概率后验测试法，检验了VaR风险度量的准确性，结果见表6（VaR估计值取正）。

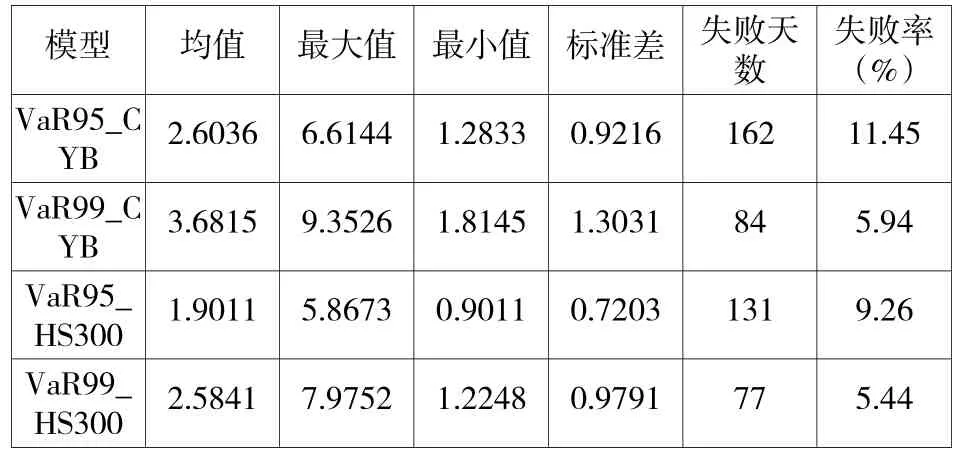
表6 GED分布下VaR估计的描述性统计及后验测试

表6结果显示：1、从VaR的均值与标准差来看，平均来说，创业板市场风险远高于主板，风险溢出率约在40%以上；2、从极端最大值来看，在99%置信水平下，VaR方法较好度量了创业板实际最大损益（-9.33%），但却低估了主板实际最大损益（-9.15%）；3、给定10%的显著水平，95%置信水平下VaR风险度量对创业板是失败的，但99%的VaR度量则较为准确；对主板指数沪深300而言，无论在95%、还是在99%置信水平下，VaR方法总体上均通过了后验测试检验，可较好度量主板市场风险。③

五、结论

自我国创业板市场推出以来，丰富了我国多层次的资本市场建设，但其呈现出的暴涨暴跌对主板市场产生着深刻影响。针对创业板与主板股指收益率的不同统计特性，本文采用FGARCH-M模型实证研究了二者的收益波动溢出效应，并用VaR模型度量了创业板与主板的市场风险。

实证研究发现：1、创业板与主板的收益之间互有溢出效应，且主板收益对创业板收益的溢出效应要更为显著；2、创业板收益率存在有明显的风险补偿机制，即创业板指波动越大、创业板指收益也越高，但主板收益并不存在这一现象；3、尽管主板对创业板指的波动溢出效应并不存在，但主板波动性却确实创业板收益变动的影响，说明二者的波动溢出效应不尽相同；4、创业板与主板的TARCH效应检验并不显著，即二者的条件波动率都不存在有"杠杆效应"，这可能与我国股市暴跌时通常有政策护盘有关；5、VaR模型总体上可较好度量创业板与主板的市场风险，平均来说，创业板指的市场风险远高于主板，风险溢出率约在40%以上。

[注 释]

①股票指数作为一定数量股票的投资组合，可度量标的市场的整体状况。故创业板与主板，可分别采用创业板指数与沪深300指数来代表反映其走势。

②限于篇幅，此处仅报告了部分滞后阶数的相关性检验Q统计量与ARCH检验LM统计量的值，其他滞后期的统计量值得出的推断结论，与报告结果一致。

③考虑到我们的样本期涵盖了2015.6月以来的3次大股灾极端市场波动情况，此处VaR的后验测试结果，验证了该方法的适用性。

[1]Jean-Michel Zakoian,Threshold heteroskedastic models[J], JournalofEconomic Dynamicsand Control,1994,(5),p931-955

[2]Panayiotis F.Diamandis,Anastassios A.Drakos,Georgios P. Kouretas,Leonidas Zarangas,Value-at-risk for long and short trading positions:Evidence from developed and emerging equity markets[J], InternationalReview of FinancialAnalysis,2011,(3),p65-176

[3]S.Stavroyiannis,I.Makris,V.Nikolaidis,L.Zarangas, Econometric modeling and value-at-risk using the Pearson type-IV distribution [J],International Review of Financial Analysis,2012,(4), p10-17

[4]耿庆峰、黄志刚，我国创业板市场股价波动风险测度研究[J]，福建师范大学学报，2013,(4)

[5]郭乃幸、杨朝军、吴海燕、刘景方，中国股市主板与创业板市场溢出效应研究[J]，上海管理科学，2013,(2)

[6]任继勤、单晓彤、梁策，中国主板与创业板市场风险比较分析--基于GARCH-VAR方法[J]，财贸研究，2015,(3)

[7]张金林、贺根庆，中国创业板和主板市场时变联动与波动溢出--基于DCC-MGARCH-VAR模型的实证分析[J]，中南财经政法大学学报，2012,(2)

[8]郑平，GARCH类模型对国沪深300指数VAR值模型的模拟估算[J]，统计与决策，2014,(14)

责任编校：徐 晓

On M arket Risk Assessmentand Fluctuation Spillover Effects ofM ain-board M arketand Second-board M arket: Based on FGARCH-M-VaRM odel

MA Jie
(Beijing University of Aeronauticsand Astronautics,Beijing,100083,China)

The papermade an empiricalstudy of the yields fluctuation spillover effects betweenmain-board and second-boardmarketsbased on FGARCH-M-VaRModeland assessed the twomarkets'riskswith VaRmodel.The study indicatesa surprising result:though there isa spillover effectbetween the twomarkets,one hasa differenteffect on the other.Main-boardmarketdidn'thave a spillover effecton the second-boardmarket;there isno leverage effect concerning conditional volatilities of the twomarkets,which may havemuch to do with the government supportive measures applied duringmarket crash.The study indicates VaRmodel could wellmeasure the risksof themain and second board markets.On the average,there ismuch more risk in the second-board market,with over 40%risk overspill rate.

thesecond-board;themain board;GARCH classmodels;valueat risk

F224；F832.51

A

2095-7955（2016）06-0039-05

教育部人文社科基金(项目编号：13YJA790082)；国家自然科学基金(项目编号：71571007)；中央高校基本科研业务费(项目编号：30-3600-01)。

2016-11-08

马 杰（1974—），北京航空航天大学经管学院数量经济与统计系系主任，副教授，博士。主要研究方向：数量经济。