概括能力在数学概念教学中的渗透

胡祝齐

数学概念是数学学科最基本、最重要的组成部分。数学概念的具体习得有两种模式：从大量实际例子出发，经过比较、反思、分类、探究等活动，找出本质属性，再通过其他例子进行检验与修正，最后概括，得到数学概念，这种称为数学概念的形成;先把概念的意义直接以定义的形式呈现给学生，学生再利用自己认知结构中已有的知识和观念理解其意义，从而获得新概念，这种称为数学概念的同化。

1.数学概念形成中概括能力的培养

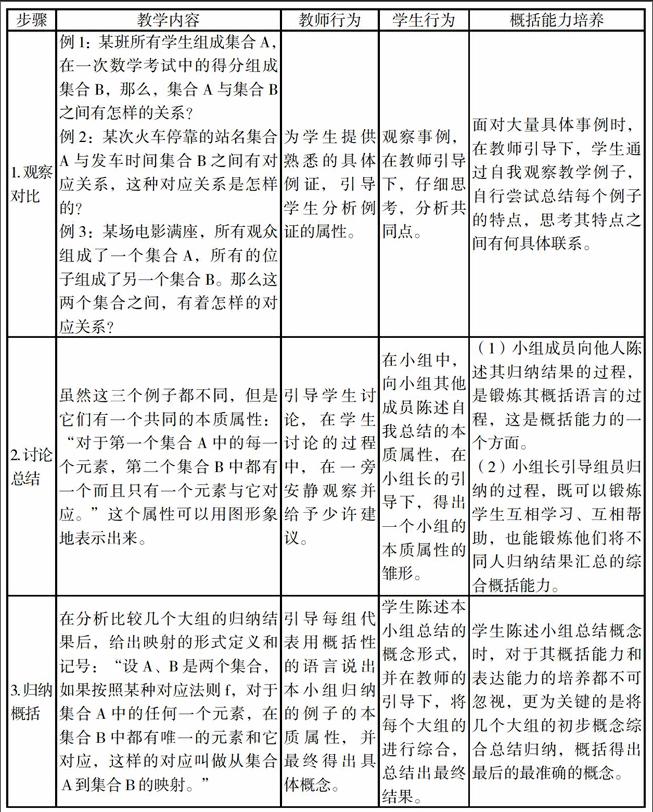
下面以映射概念为具体例子（见下表）。

2.数学概念同化中概括能力的培养

下面以幂函数的概念为具体例子。

（1）概括旧知。学生在其自我数学知识体系的基础上，概括已经学习的指数函数和对数函数的概念，并比较它们的不同。其中重点归纳指数函数的特殊性。

【概括能力培养1】

学生用自己的语言陈述已学过的数学概念的过程，实质是学生用语言提炼和概括自己脑海内知识体系的过程。学生不可以用书上的原本概念回答，必须用自己的语言表达出同样的意思，强调概念的原创概括性。

（2）解释新知。在学生基本明了指数函数和对数函数的概念后，教师将幂函数的概念在黑板上给出：一般地，形如y=xa（a为常数）的函数，称为幂函数。引导学生比较幂函数和指数函数的区别，给出幂函数图象。

学生对照教师给出的幂函数概念和图象，回顾前一阶段自己概括的旧知识，在旧知识的基础上，发掘新知识（幂函数概念）和旧知识（指数函数）的区别，找出两者本质属性的不同之处、相似之处和易混淆之处。

完成自我比较新旧知识后，学生向全班展示其发掘的关键概念并给出易混淆的点。最后在教师的引导下，全班对幂函数的概念进行充分剖析，并掌握新概念（幂函数）与旧概念（指数函数）的不同，突出两者的关键属性和易混淆点。

【概括能力培养2】

学生在自我对比新旧概念的过程中，需要在自己的知识理解的基础上，概括出新概念与旧概念的不同，总结归纳出新概念的关键属性以及两者的易混淆点。

总之，数学概念的形成教学形式相对于低年级的学生较合适，因为概念形成的方式类似于人类自身发现知识的过程，丰富的例证对低年级学生的概括能力很有帮助;而数学概念的同化教学形式更适合高年级学生，这是考虑到学生理解力和掌握力的提升得出的。相比来说，概念同化中概括能力的培养更高级、也更有效。

（作者单位：江西师范大学附属中学）