基于《图形的认识》课例的数学大问题设计与解决策略的课例研究报告
2016-03-12欧阳小珠付维欧阳兰桂
欧阳小珠+付维+欧阳兰桂

一、课例研究背景
1.课例研究的提出
新课程倡导学习的发展功能,关注学生在学习数学中的发展,注重学习的过程,“使每一个学生在数学学习中都能有所发展,不同的学生在学习中得到不同的发展”。这就要求我们教师改变“教师讲、学生听”的注入式教学方式,体现学生的主体地位;给学生提供自主探究、合作交流的时间和空间,培养学生发现问题的能力,调动学生学习的积极性和主动性,减轻学生的学习负担。
近年来,湖南省株洲市芦淞区积极创建的“主体性”课堂,更是直面课堂,要求彻底改变教与学的方式,要求以学生为主体,促进学生全面发展。课堂中为学生提供有探究价值的高效问题,是突出学生主体地位的关键。大量教学实例表明,教师在教学实践中并非没有问题或不设计问题,而是问题设计不成章法或随意而为,如问题琐碎、思维质量较低,问题给学生思考空间不大,问题指向性不明确,问题难度控制不当,问题导向重思维结果、轻思维过程等。在借鉴芦淞区教研室已有经验的基础上,进一步设计数学大问题并运用大问题的策略来提高课堂教学的有效性,就成为我们本次课例研究的初衷。
2.教学现状的分析
湖南省株洲市芦淞区何家坳小学(以下简称“我校”)数学团队共有27名成员,其中市级数学学科带头人1名,区级教育名师、骨干教师6名,芦淞教坛新秀2名。这支队伍老中青年龄结构合理,教师个人素质过硬,教师们在教学的同时致力于教学研究,特别是近几年来更是取得了令人瞩目的成绩。
就我校数学课堂针对图形与几何的教学现状来看,许多教师重知识结果而轻过程性教育,重知识技能而轻思维能力的培养,重点形式化,内容比较单调,呈现的方式也是冷冰冰的,难以激发学生的学习欲望和兴趣,难以发挥学生的主动性和创造性。
基于上述思考,我们拟通过课例研究的形式,立足小学数学“图形与几何”教学板块的教学与研究,对数学课堂教学的大问题设计进行探索和实践,促进教师的专业发展,全面提高学生的数学素养。
二、主题的界定
1.“大”问题设计
“大”问题应是思维容量大、能够统领课堂教学、能在最大限度上让学生的能力得到发展的问题。这个问题要围绕教学目标,能最好地解说教材,从教材整体的角度和学生的整体参与性上引发学生思考、讨论、理解、感悟、探究、应用,并能促进学生完成学习任务,促进学生成长发展。它是相对于教学过程中的“连问”、简单应答的“碎问”以及随意的“追问”而言的。
2.大问题解决策略
大问题解决策略包含两个方面:一是教师围绕本课的教学目标以及重难点而设计的教学活动;二是根据学生的学习状况以及思维水平而随机采用的教学方法和调控策略。
3.明确图形认识教学
图形及其性质的认识是图形与空间领域中的重要内容之一。学生将在现实生活中已经积累了一些基本图形的认识经验的基础上,用数学的眼光去重新认识常见的立体图形和平面图形;在丰富的现实背景中,通过观察、操作、比较、概括、推理等探索常见图形的性质,并运用它们解决实际问题;在立体图形和平面图形转化等活动中,建立空间观念;在欣赏丰富多彩的图形的同时,体会图形在现实世界中的广泛存在。
三、课例研究过程
(一)探索归纳阶段(《认识四边形》为课例)
1.选课与析课
(1)选课背景。教师在教学图形的认识中往往非常注重学生通过观察、操作、测量等活动积累感性经验,而忽视比较、概括、分析、推理等思维含量比较高的理性抽象。我们数学组以打造“主体性课堂”为导航,根据芦淞区教育局提出的“主体性课堂”教学、株洲市教科院提出的“如何在数学教学中发展学生的思维能力”这一专题,以“图形的认识”为载体,探寻大问题的设计以及实施策略。刘芳老师《认识四边形》课例的形成正体现了这一点。
(2)教学目标的认知和制订。教学目标是设计大问题之魂,因此对于目标的制订,我们从以下方面进行了分析:①已有的知识基础:在低年级,学生已经认识了基本的平面图形,如圆形、三角形、长方形、正方形、平行四边形;也初步认识了立体图形,如长方体、正方体、圆柱体、球体。并且在生活中积累了很多这些二维、三维图形的经验。②知识体系中的地位:《认识四边形》是对低年级所学平面图形的一个综合性认识,让学生把所学的平面图形分类,找出四边形的共性,同时教材从一般四边形的特征到特殊四边形的特征探究,从共性到个性,从一般到特殊,都是对后面平行四边形和长方形、正方形周长的计算奠定知识基础。③教学内容例题安排及其目的:主题图是一幅校园场景图,图上有许多关于“空间与图形”的信息。如:长方形的篮球场、通道、窗户,正方形的地砖,平行四边形的推拉门、楼梯护栏,等等。目的是联系学生的生活经验,丰富他们对图形特别是四边形的感性认识,并从整体上感知自己生活中的几何图形。
基于以上分析,我们遵循孩子们的认知规律,从具象到抽象,从一般到特殊,将知识与技能的教学与能力情感的培养有机结合,特将目标制订如下:
知识与能力:观察感知四边形,能区分和辨认四边形,了解四边形的特征,知道长方形和正方形是特殊的四边形。
过程与方法:通过找一找、涂一涂、画一画、分一分等活动,培养学生观察、比较、分析、概括、抽象的能力,进一步发展空间观念。
情感态度与价值观:通过情境图和生活中的事物进入课堂,感受生活中的四边形无处不在,让学生感受数学的奥秘,体验数学的形态美与内涵美。
2.磨课与议课
(见右表)
3.归纳与提炼
根据三次磨课与教师的讨论,我们提炼出《图形的认识》教学中可以在教材的缺乏处、思想方法的凝结点、学生的疑难处提出大问题。在《图形的认识》教学中我们组织学生围绕大问题,采用将大问题的设计和情境紧密结合起来,让学生经历辨析、分类的过程等策略,以引导学生解决大问题,建立数学模型。
(二)验证提升阶段
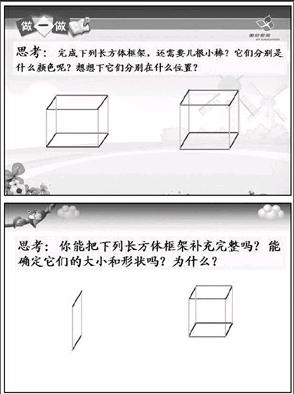
根据前一阶段的课例研究的结论,我们运用《长方体的认识》进行了验证。在这节课中教师提出了这么一个问题:“你能把下列长方体框架补充完整吗? 能确定它们的大小和形状吗?为什么?”教材中没有提到长方体的长、宽、高会影响长方体的形状和大小,这就是利用教材的缺乏处提出大问题。在探究棱的特征时,教师提供了长短不一的小棒让学生搭建长方体框架,然后提出问题:“这些小棒你可以分为几类?”让学生观察、比较、分析、归纳出棱的特征,这是在思想方法的凝结点提出大问题。在探究长方体面的特征时,学生提出:“是否所有长方体的每个面都是长方形呢?”这是在学生的疑难处提出了大问题。
教师评课记录:
(1)从问题情境出发,由已知的长方形,引导学生认识长方体,善于倾听学生的独特见解并适时追问和点拨,注重对学生引导,体现了以学生为主体。学生在原有的基础上获得了知识与技能、过程与方法、情感态度与价值观等方面的发展。
(2)由面到体的变化激发学生的学习兴趣,使学生对长方体有一个初步的认识;由实物抽象出体,学生易于接受;制作长方体框架活动,让学生对长方体特征的认识更加清楚,理解更加透彻。但检测题有点难,建议可利用长方体框架感受棱长总和。
(3)教师的大问题设计合理,扣住了本节课的教学目标;解决大问题的策略主要有展示交流、动手操作、类比推理,教师在实施的过程中,追问有待精简;练习设计比较有梯度,开放而灵活;教师在学生分析归纳时,可让学生多说,应表述完整。
四、研究的结论
小学数学《图形的认识》核心知识包括以下五个方面:图形的抽象、图形的分类、图形的定义、图形的性质、图形的转化。通过《认识四边形》三次授课以及《长方体的认识》的验证课,老师们有了深刻的认识。特别是对大问题的特征,大问题该怎样设计,该怎样实施才能达到发挥学生思维能力与主动性有了深刻的认识。
1.大问题的特点
(1)具有开放性。例如,《认识四边形》例题2,渗透了分类思想、归纳推理的思想,还有折、比、量这些科学探究的方法。
(2)具有生成性。例如,在探究长方体面的特征时,学生提出:“是否所有长方体的每个面都是长方形呢?”教师根据学生的提问组织学生观察特殊的长方体,然后归纳出特殊长方体的面的特征。
(3)具有挑战性。例如,在《长方体的认识》教学中,教师设计了这么一个问题:“你能把下列长方体框架补充完整吗?能确定它的大小和形状吗?为什么?”(图略)
2.大问题的设计策略
(1)在教材的缺乏处提出大问题。例如,在本节课中,没有给四边形下定义的语言,纵观小学教材,很多概念的给出都是描述性语言。那么,本节课的大问题“什么是四边形”概念的给出就是对教材缺乏的补充。
(2)在学生学习的疑难处提出问题。
(3)在思想方法的凝结点处提出大问题。例如,本节课中,给四边形分类,提出:“为什么你们把它们分成一类呢?它们有什么共同特征呢?”
3.图形认识教学中大问题教学的策略
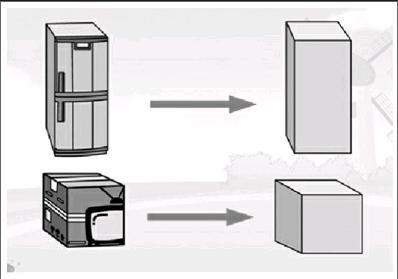
(1)将大问题的设计和情境紧密结合起来。比如,在《长方体的认识》一课中,开始是这样设计的:“在我们的生活中有哪些物体的形状是长方体的呢?指名举例。”(教师可以随机出示几张长方体实物图)课件如下图。
(2)经历辨析、分类的过程,引导学生围绕“大问题”的探究总结概括思想与方法。
如在《认识四边形》一课中,关于四边形的分类,教师是这样设计的。
第一步:引出问题。
师:刚刚同学们在生活中找了很多四边形,也了解了什么是四边形和四边形的特征,现在,这些四边形想请你们帮帮忙,给它们分类。
第二步:提出分类任务。
小组合作要求:请你选择好工具,定好分类的标准;组长组织组员分类,用自己喜欢的方式记录;推荐两名同学汇报,一名说分类理由,一名摆出分类情况。
温馨提示:用三角尺的直角去比一比这些四边形角的大小;用折一折、量一量的方法,去比一比边的长短。
第三步:交流与汇报。
按角分:长方形、正方形(四个角都是直角)。
菱形、平行四边形、不规则四边形、梯形(没有直角)。
按边分:长方形、正方形、平行四边形、菱形(两组对边相等)。
梯形、不规则四边形(两组对边不相等)。
正方形、菱形(四边相等)。
不规则四边形、梯形(四边都不相等)。
按对角分:长方形、正方形、平行四边形、菱形(对角相等)。
不规则四边形、梯形(对角不相等)。
在学生分的过程中,一步一步解决一些最基本的四边形的特征(上下为一组对边,左右为另一组对边)以及特殊四边形的特征(长方形与正方形的特征)。
(3)经历图形的转化过程,发展空间观念。在《数学课程标准》中关于空间观念是这样叙述的:主要是指能根据物体特征抽象出几何图形,根据几何图形想象出所描述的实际物体;想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形。
在《长方体的认识》一课中,教师是先动手制作长方体框架以初步形成空间观念,然后设计以下两道练习题,层层递进,发展学生的空间观念。
(作者单位:湖南省株洲市芦淞区何家坳小学)
