考虑桥梁限重标志对驾驶员行为约束的车辆荷载效应研究

邓露　毕涛　何维

摘 要：通过对某市货车驾驶员进行问卷调查，研究了桥梁限重标志对货车驾驶员驾驶行为的约束作用规律；基于实测随机车流的统计分布规律，利用蒙特卡洛法编写了考虑桥梁限重标志对驾驶员行为约束作用的随机车流模拟程序.以55t桥梁限重值为例，根据《公路工程结构可靠度设计统一标准》的荷载效应分析方法，计算了简支梁桥在模拟随机车流荷载作用下的跨中弯矩和支座剪力.对日均交通量、条件约束水平和桥梁跨径进行了参数分析，并将随机车流荷载作用下的荷载效应与中国现行桥梁设计规范中对应的汽车荷载效应标准值做了比较.研究结果表明：1）只有当超重货车驾驶员均严格遵守桥梁限重规定时，桥梁限重标志才能有效地控制车辆荷载效应，从而保障桥梁的安全可靠性；2）中国现行桥梁设计规范的设计荷载可能低估了某些路段实际车流的荷载，且在小跨径桥梁上尤为突出，应当引起重视.

关键词：桥梁工程；车辆荷载效应；蒙特卡洛法；简支梁桥；限重标志；驾驶员行为

中图分类号：U447 文献标识码：A

文章编号：1674-2974（2015）11-0049-07

近年来随着我国经济的高速发展，公路交通运输量和车辆荷载均逐年增大，各地车辆超重现象普遍，严重影响了在役桥梁的安全可靠性[1].由超重车引起的桥梁垮塌事件屡见不鲜，如2009年黑龙江省伊春市的铁力西大桥和2011年北京市的怀柔白河桥的垮塌事故等[2-3].为了保障在役桥梁的安全可靠性，近年来全国多地投入了大量财力物力对在役桥梁进行限重，如2009年青岛为本市桥梁增设了239块限重标志牌，以及2011年浙江对省内所有普通国、省道上的3894座桥梁设置了限重标志进行限重.

近年来国内外学者对桥梁限重问题进行了广泛研究.Nowak等[4]基于实测车辆动态称重（WIM）数据研究了公路桥梁的货车荷载谱，Fu等[5-6]也进行了相关研究.Ghosn和Moses[7-9]应用结构可靠度理论分析了现行桥梁限重公式的可靠性，提出了具有规定可靠性水平的桥梁限重建议公式.宗雪梅等[1]利用等代荷载法计算超重车辆荷载模型的限载系数最终确定超重车辆的限载值.Correia等[10]基于超重车的统计特性和车辆荷载效应简化分析方法，根据安全系数判别超重车是否过桥.王硕[11]利用对实桥交通荷载模型进行修改试算的方法来确定桥梁限重值，为《上海市城市桥梁限载技术标准》提供了理论依据.王松根与李松辉[12-14]根据公路桥梁抗力及荷载效应的概率分布函数与统计参数提出了一种基于结构可靠度理论的典型车辆限重分析方法.

然而，极少有研究考虑到实际交通管理中桥梁限重规定的执行效果，即并非所有的驾驶员都一定会严格遵守桥梁限重规定.如2004年辽宁盘锦境内田庄台大桥由于一辆总重110t的大货挂车严重超重导致桥梁垮塌，而相关部门早在2000年7月就对该桥实施了限重15吨的规定.因此，设置桥梁限重标志对保障桥梁的安全可靠性所发挥的实际作用值得研究.目前仅Astantey[15-16]以一种典型货车为对象研究过超重车违规率对过桥货车的车重分布规律以及对简支梁桥结构可靠度的影响，且在研究中假设所有超重车过桥的概率都相同，这与实际情况有较大出入.

本文通过对某市货车驾驶员进行抽样问卷调查分析了桥梁限重标志对驾驶员驾驶行为的主观约束效果.根据基于WIM数据得到的自然随机车流统计参数，利用MATLAB语言编制了考虑限重标志对驾驶员行为约束的随机车流模拟程序和桥梁影响线加载程序，模拟多种状况下的随机车流，计算了中小跨径简支梁桥在模拟生成的随机车流荷载作用下的荷载效应，并与中国现行的桥梁设计规范[17]中对应的汽车荷载效应标准值进行对比.从而探讨桥梁限重规定（标志）对限制超重车过桥和保障桥梁安全所发挥的真实作用.

1 基于统计调查研究限重标志对驾驶员行

为的主观约束效果

桥梁限重标志对驾驶员驾驶行为的约束可归纳为客观约束和主观约束.客观约束指国家相关管理部门的规定及行政执法等客观因素对驾驶员过桥行为的约束；主观约束指驾驶员考虑所驾车的超重水平后对其过桥行为的约束.前者侧重管理部门干预和处罚的客观影响，后者侧重驾驶员自身对安全驾车过桥的主观考虑.

考虑到在真实交通中调查桥梁限重标志对驾驶员行为主观约束作用的困难性，2013年，本文通过抽样问卷调查的方式研究了桥梁限重标志对驾驶员行为的主观约束规律，本问卷只调查驾驶员的主观约束行为，不考虑客观约束的影响.调查对象为某市的货车驾驶员.有两点假设：1）假设客观约束和主观约束相互独立；2）假设主观约束行为只跟货车总重有关，与货车车型无关.

本次调查一共发放问卷250份，有效反馈问卷194份.调查内容分为两部分，第一部分为驾驶员的基本信息，包括驾龄、所开货车的种类及装载物等；第二部分为与超重相关的内容，包括是否会留意桥梁限重标志、超重经历、超重的原因、在桥梁不同限重水平下意愿驾驶车过桥的车重等.通过SPSS 19.0统计分析软件对调查问卷数据进行统计分析显示：被调查者中驾龄为1～5年的占20.6%，6～10年的占35.6%，11～15年的占30.9%，大于16年（含）的占12.9%，说明被调查者的驾龄分布广泛且各自所占比例较为平均；大部分驾驶员都有过驾驶超重车的经历，并且一般都会留意桥上的限重牌；78%的货车超重时装载的货物为煤、建材或机械设备，其超重的原因主要包括两方面：一是迫于较高的运营成本和竞争压力，若不超重公司（或个人）的盈利率低，其比例占49.5%；二是驾驶员认为桥梁承载力具有一定的安全系数（即规定的桥梁限重值是偏安全的），其比例占21.6%.

对调查问卷结果进一步整理分析获得了当桥梁限重分别设为10 t，15 t，20 t，30 t，40 t和55t时，货车总重与驾驶员意愿驾车过桥的概率之间的关系.并利用MATLAB曲线拟合工具中的幂函数、多项式和指数函数等函数对统计结果进行了曲线拟合.根据拟合优度的判定准则（包括残差平方和（SSE）、均方根误差（RMSE）和调整的判定系数（Adjusted R-square）等）对拟合结果进行评价，发现用幂函数拟合的效果最优.

幂函数表达式为f.L（x）=αxβ，其中x表示货车总重（x≥L），L表示桥梁限重值（x，L的单位为吨（t）），α和β为幂函数的参数，f.L（x）表示驾驶员意愿驾车过桥的概率.在不同限重水平下，驾驶员意愿驾车过桥的概率与货车总重的关系的曲线拟合结果见图1，其中散点为调查问卷统计结果，实线为拟合曲线.从图1可以发现，在不同的限重水平下，驾驶员意愿驾车过桥的概率与货车总重的关系有相似的规律：随着货车车重的增加，驾驶员意愿驾车过桥的概率下降较为明显，到最后逐渐趋近于零.但值得注意的是，当车重达到限重值的两倍时，驾驶员意愿驾车过桥的概率仍在10%以上，说明桥梁限重标志对货车驾驶员行为的主观约束作用是有限的.

2 考虑驾驶员行为约束的随机车流模拟

为了研究限重标志引起的驾驶员行为约束对随机车流变化的影响，首先基于对WIM数据进行统计分析获得的真实车流统计特性（轴距、车头间距和车重等参数），利用蒙特卡洛法[11]（Monte Carlo Method，简称M-C法）生成大量与真实车流具有相同统计规律的模拟随机车流样本，然后根据问卷调查的统计分析结果对模拟随机车流样本进行修正，从而获得考虑了限重标志对驾驶员行为约束的修正随机车流.

2.1 自然随机车流的统计参数

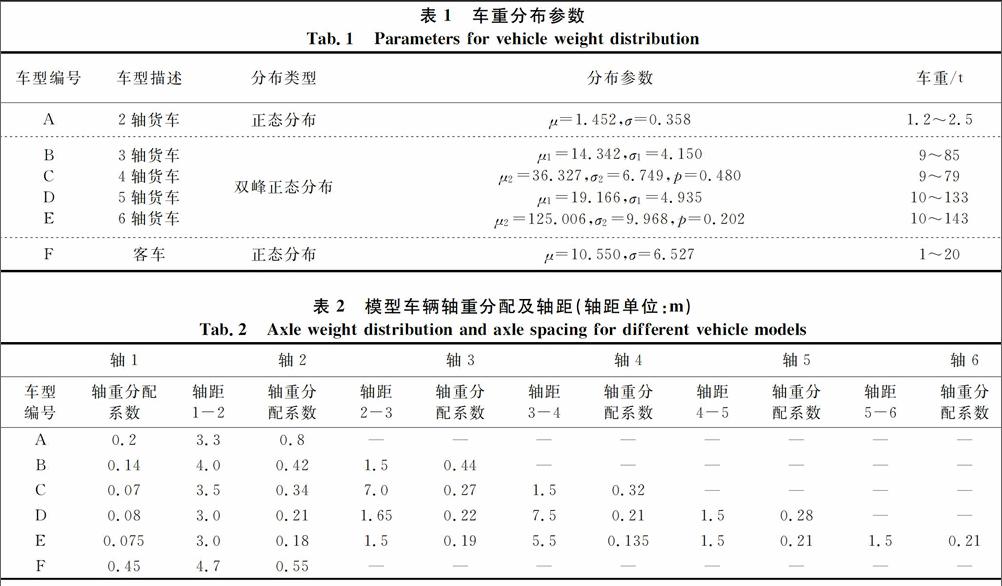
选取梁栋等[18]于2008年通过WIM调查得到的某Ⅰ级公路自然随机车流的统计参数作为模拟随机车流的源数据.车头间距服从对数正态分布，参数为μ=2.873 1，ν=0.620 1.模型车辆共6种，分别用A～F表示，各模型车辆的车辆总重的分布类型及相关参数见表1；各模型车辆的轴重分配系数及轴距见表2；模型车辆A～F在随机车流中所占比例分别为20.0%，15.3%，12.6%，15.1%，16.6%和10.4%.

2.2 绝对约束和条件约束

为研究超重车驾驶员受桥梁限重标志主观约束的水平对随机车流以及车辆荷载效应的影响，将主观约束分为绝对约束和条件约束，分别用R.A和R.I表示：

R.A=（N.A/N）×100%； （1）

R.I=（N.I/N）×100%.（2）

式中：N.A为任何超重水平下均能严格遵守限重规定的超重车驾驶员人数；N.I为根据实际超重水平再决定是否违规过桥的超重车驾驶员人数；N为超重车驾驶员总人数.显然，R.A和R.I的取值范围均为＼[0，1＼]，且有R.A+R.I=1.

2.3 模拟随机车流的基本流程

基于实测随机车流的统计参数，用MATLAB语言编写考虑桥梁限重标志对驾驶员行为约束的随机车流模拟程序.首先模拟生成初始随机车流，然后考虑桥梁限重标志对驾驶员的行为约束从而对初始随机车流进行修正，基本流程如图2所示.

图2中，rand（1，1）是MATLAB库函数，作用为生成服从区间（0，1）上均匀分布的随机数.超重车驾驶员受绝对约束或条件约束由条件“rand（1，1）≤R.I”判定，若该式成立则表示该超重车驾驶员会考虑车辆实际超重水平再决定是否过桥，反之则表示该超重车驾驶员会严格遵守限重标志而不过桥.受条件约束的超重车驾驶员决定是否过桥由条件“rand（1，1）≤f.L（x）”判定，该式若成立则表示该超重车驾驶员在考虑所驾车的实际超重水平后最终决定驾车过桥，反之则最终决定不过桥.

3 车辆荷载效应分析

3.1 利用影响线对桥梁进行随机车流荷载加载

假定随机车流在桥上通过时保持横向位置不变，且不考虑结构非线性对荷载效应的影响，则可利用影响线对桥梁进行随机荷载流加载并得到相应截面的荷载效应.常见加载程序的基本思路[3，18-19]如下：1）计算控制截面响应的影响线；2）将生成的随机车流沿影响线以步长d.s（d.s的值一般取为10 cm）移动，计算每一步的车辆荷载效应，并记录目标周期（一般以日为时间周期）内的车辆荷载效应最大值；3）重复步骤2），得到n个目标周期内的最大荷载效应值.

3.2 不同条件约束水平下日均交通量对控制截面荷载效应的影响

选取跨径为20 m，限重L=55 t的简支梁桥为研究对象，利用《公路工程结构可靠度设计统一标准》（GB/T50283-1999）[20]的荷载效应分析方法，考察单车道加载下桥梁的跨中弯矩和支座剪力.本文计算了日均交通量分别为500，1 000，2 000，4 000辆时不同R.I水平（0，0.025，0.05，0.1，0.3，1）下的桥梁荷载效应，并在各种情况下均对桥梁加载20000日.为便于将随机车流荷载作用下的荷载效应与中国现行桥梁设计规范进行对比研究，引入无量纲荷载效应比值K：

K=S.Q/S.QK.（3）

式中：S.Q表示模拟随机车流荷载作用下的荷载效应最大值分布的95%分位值，S.QK表示中国现行桥梁设计规范中公路Ⅰ级荷载对应的汽车荷载效应标准值.K.M表示基于跨中弯矩计算得到的荷载效应比值，K.Q表示基于支座剪力计算得到的荷载效应比值，两者在不同R.I水平下与日均交通量的关系如图3和图4所示.不难发现：1）随着日均交通量在区间＼[500，4 000＼]上逐渐增大，K.M和K.Q均逐渐增大，当日均交通量大于2 000辆后，曲线走势趋于平缓，说明随着日均交通量的增大，日均交通量对K.M和K.Q的影响逐渐变小；2）K.M和K.Q随着R.I的减小而减小，但起初减速比较缓慢；当R.I从0.025降为零时，K.M和K.Q突然有明显减小，说明只有当超重车驾驶员均严格遵守桥梁限重规定时，才能有效控制车辆荷载效应.此外，值得注意的是，在基于实测数据模拟生成的随机车流作用下，K.M和K.Q的值均大于1.表明我国现有规范中的标准荷载可能低估了某些桥梁上实际车流的荷载.因此实际车流作用下桥梁的荷载效应应该引起工程界深刻的关注.

3.3 不同条件约束水平下桥梁跨径对控制截面荷

载效应的影响

选取跨径增量为5 m的10～50 m的9座简支梁桥为研究对象，日均交通量为2 000辆，计算不同R.I水平下的K.M和K.Q值，结果如图5和图6所示.从整体上来看，随着跨径的增加，K.M和K.Q逐渐降低，但当R.I≠0时，在小跨径区段＼[10，20＼]内，K.M和K.Q值的变化并无明显规律，说明中国现行桥梁设计规范对小跨径桥梁的汽车荷载考虑相比其他跨径可能不足，文献＼[21＼]也有相似的结论.此外，本文所采用的模拟随机车流数据来源于交通实测统计数据，而图5和图6均显示，即使当R.I等于零时，K.M和K.Q的值仍然大于1，说明中国现行桥梁设计规范的设计荷载效应可能低估了某些桥梁上实际车流的荷载效应，并且剪力效应更加明显.

4 结 语

本文基于对货车驾驶员的问卷调查，研究了桥梁限重标志对货车驾驶员过桥行为的约束作用.编写了考虑桥梁限重标志对驾驶员行为约束的随机车流模拟程序.以55 t桥梁限重值为例，分析了日均交通量、条件约束水平和桥梁跨径对简支梁桥跨中弯矩和支座剪力的影响，并与中国现行桥梁设计规范的弯矩标准值和剪力标准值做了比较.值得说明的是，本文是基于对某一城市货车司机的调查问卷结果来分析桥梁限重标志对货车驾驶员过桥行为的约束作用规律的，其调查结果并不一定能完全准确地反映真实情况.本文旨在初步探索由桥梁限重规定（标志）对驾驶员主观驾驶行为的影响而产生的对桥梁上车辆荷载效应的影响.本文获得了如下主要结论：

1）桥梁限重标志对货车驾驶员驾驶行为的约束作用是有限的.在不同的限重水平下，总有相当数量的驾驶员意愿驾驶超过限重值一倍以上的货车过桥；并且，在不同限重水平下，驾驶员意愿驾车过桥的概率与货车总重的关系有相似的规律，均可用幂函数来描述.

2）只有当超重车驾驶员均严格遵守桥梁限重规定时，才能有效控制车辆荷载效应，否则，桥梁限重达不到预期效果.因此，在交通管理中，必须严格执行桥梁限重规定，以保障桥梁的安全可靠性.

3）本文所采用的随机车流数据来源于实测交通统计数据.而本文研究发现，即使驾驶员严格执行限重规定，随机车流产生的荷载效应仍大于规范标准值，说明中国现行桥梁设计规范的设计荷载可能低估了某些桥梁上实际车流的荷载，且在小跨径桥梁上尤为突出，应当引起重视.

参考文献

[1] 宗雪梅， 胡大琳， 高军. 桥梁超重荷载与限载标准的确定[J]. 长安大学学报： 自然科学版， 2008， 28（1）： 60-65.

ZONG Xue-mei， HU Da-lin， GAO Jun. Vehicle's overload and limiting load standard for bridge safety[J]. Journal of Chang'an University： Natural Science Edition， 2008， 28（1）： 60-65. （In Chinese）

[2] 吉伯海， 傅中秋. 近年国内桥梁倒塌事故原因分析[J]. 土木工程学报， 2010， 43（1）： 495-498.

JI Bo-hai， FU Zhong-qiu. Analysis of chinese bridge collapse accident causes in recent years[J]. China Civil Engineering Journal， 2010， 43（1）： 495-498. （In Chinese）

[3] 党栋. 公路桥梁设计荷载及其组合研究[D]. 西安： 长安大学， 2012：4-7.

DANG Dong. Study on the highway bridge design load and there combination effect[D]. Xi'an： Chang'an University， 2012：4-7. （In Chinese）

[4] NOWAK A， NASSIF H， DEFRAIN L. Effect of truck loads on bridges[J]. Journal of Transportation Engineering， 1993， 119（6）： 853-867.

[5] FU G， HAG-ELSAFI O. Vehicular overloads： load model， bridge safety， and permit checking[J]. Journal of Bridge Engineering， 2000， 5（1）： 49-57.

[6] FU G， FENG J， DEKELBAB W， et al. Impact of commercial vehicle weight change on highway bridge infrastructure[J]. Journal of Bridge Engineering， 2008， 13（6）： 556-564.

[7] GHOSN M.， MOSES F. Effect of changing truck weight regulations on US bridge network[J]. Journal of Bridge Engineering， 2000， 5（4）： 304-310.

[8] GHOSN M. Development of truck weight regulations using bridge reliability model[J]. Journal of Bridge Engineering， 2000， 5（4）： 293-303.

[9] MOSES F， GHOSN M. Discussion of "proposed new truck weight limit formula" by Ray W. James， James S. Noel， Howard L. Furr and Francisco E. Bonilla （July， 1986， Vol. 112， No. 7）[J]. Journal of Structural Engineering， 1987， 113（11）： 2330-2331.

[10]CORREIA J， BRANCO F. New methodology： permit checking of vehicular overloads[J]. Journal of Bridge Engineering， 2006， 11（3）： 274-281.

[11]王硕. 桥梁运营荷载状况研究[D]. 上海： 同济大学， 2007：58-80.

WANG Shuo. Study on load condition for in-service bridges[D]. Shanghai： Tongji University， 2007： 58-80. （In Chinese）

[12]王松根， 李松辉. 公路桥梁限载标准的可靠性分析方法[J]. 工程力学， 2010， 27（10）： 162-166.

WANG Song-gen， LI Song-hui. Reliability-based analysis on the vehicle weight limit of highway bridges[J]. Engineering Mechanics， 2010， 27（10）： 162-166. （In Chinese）

[13]李松辉. 公路桥梁限载取值的可靠性分析模型研究[J]. 土木工程学报， 2013，46（9）： 83-90.

LI Song-hui. Reliability-based analytical model for determining the truck weight limits on highway bridges[J]. China Civil Engineering Journal， 2013，46（9）： 83-90. （In Chinese）

[14]李松辉. 基于车辆荷载效应截尾分布的桥梁限载分析方法[J]. 工程力学， 2014，31（2）： 117-124.

LI Song-hui. Analytical approach for determining truck weight limits with truncated distributions of live load effects on highway bridges[J]. Engineering Mechanics， 2014，31（2）： 117-124. （In Chinese）

[15]ASTANTEY S. BARTLETT F. Impact of posted load limits on highway bridge reliability[J]. Journal of Bridge Engineering， 2005， 10（3）： 321-330.

[16]ASTANTEY S. Traffic load enforcement for bridge and highway management[D]. London：University of Western Ontario， 2002：49-88.

[17]JTGD60-2004 公路桥涵设计通用规范 [S].北京：人民交通出版社，2004：23-27.

JTGD60-2004 General code for design of highway bridges and culverts[S].Beijing：China Communications Press， 2004：23-27. （In Chinese）

[18]梁栋， 董春霞， 赵少伟， 等. 适用于重载交通的公路桥梁荷载标准研究[J]. 公路， 2011（3）： 30-36.

LIANG Dong， DONG Chun-xia， ZHAO Shao-wei， et al. Research on load standard of highway bridges suitable for heavy load traffic[J]. Highway， 2011（3）： 30-36. （In Chinese）

[19]梁玉照. 公路桥梁汽车荷载标准值取值方法研究[D]. 西安： 长安大学， 2011：42-44.

LIANG Yu-zhao. Calculation method for characteristic value of vehicle load of highway bridges[D]. Xi'an： Chang'an University， 2011：42-44. （In Chinese）

[20]GB/T50283-1999 公路工程结构可靠度设计统一标准 [S].北京：中国计划出版社，1999：12-15.

GB/T50283-1999 Unified standard for reliability design of highway engineering structures[S].Beijing：China Planning Press， 1999：12-15. （In Chinese）

[21]张征文， 杨飞， 赵建峰， 等. 基于WIM数据的简支梁桥车辆荷载效应分析[J]. 公路交通科技， 2014（5）： 86-92.

ZHANG Zheng-wen， YANG Fei， ZHAO Jian-feng， et al. Analysis on traffic load effect of simply supported beam bridge based on WIM data[J]. Journal of Highway and Transportation Research and Development， 2014（5）： 86-92. （In Chinese）