二项式定理考查题型分析

二项式定理考查题型分析

◇河北高云峰

1求指定项的系数问题

此类问题属于高考常考题型,解题中只要准确把握二项式展开式的通项公式,观察出相应的项,即可顺利求解.

由题可知

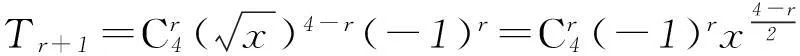
2二项式系数最大项问题

A180;B90;C45;D360

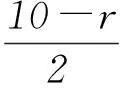
变式(2013年新课标Ⅰ卷) 设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b,若13a=7b,则m=().

A5;B6;C7;D8

3二项式系数和问题

例3若(x2+1/x3)n展开式的各项系数之和为32,则n=______,其展开式中的常数项为________.(用数字作答)

由2n=32得n=5．利用通项公式

由二项式系数的性质得到方程22n-1-2n=112解出n值;再由二项式系数取在r=n/2处(n为偶数)或r=(n±1)/2处(n为奇数)求得r值;最后再根据1120为常数项,获得通项中x的指数为0这一信息列出方程求出x的值.

由题意知22n-1-2n=112,所以

(2n)2-2·2n-224=0,

所以

(2n-16)(2n+14)=0.

又因为2n>0,所以2n-16=0,则n=4,2n=8.

又设(2x+xlgx)8的通项为

当r=8/2=4时,二项式系数最大项为

所以1120x4+4lgx=1120,也即x4+4lgx=1,所以4+4lgx=0,所以lgx=-1,则x=1/10.

4项的系数和问题

此类问题的求解通常利用赋值法,即令其中的变量为0或1或-1,进而得出各项的系数和．

例4x(1-mx)4=a1x+a2x2+a3x3+a4x4+a5x5,其中a2=-6,则实数m的值为____________;a1+a2+a3+a4+a5的值为________.

a1+a2+a3+a4+a5=1×(1-3/2)4=1/16．

变式1(x+a/x)(2x-1/x)5的展开式中各项系数的和为2,则该展开式中常数项为().

A-40;B-20;C20;D40

对式(x+a/x)(2x-1/x)5,令x=1得1+a=2,故a=1.(2x-1/x)5的展开式的通项为

由于(2x-1/x)5展开式不能产生常数项,故要得到展开式的常数项,只能x+1/x的x与(2x-1/x)5展开式的1/x相乘,x+1/x的1/x与(2x-1/x)5展开式的x相乘,故令5-2r=-1得r=3,令5-2r=1得r=2,从而可得常数项为

变式2(2015年新课标Ⅱ卷)(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=________.

由已知得(1+x)4=1+4x+6x2+4x3+x4,故(a+x)(1+x)4的展开式中x的奇数次幂项分别为4ax、4ax3、x、6x3、x5,其系数之和为

4a+4a+1+6+1=32,

解得a=3.

高考对二项式定理的考查,主要是以其展开式及通项公式为背景,以容易题、客观题为主,有时也与其他知识,如函数、不等式、杨辉三角等知识相交会,本文不再列举,请读者自行归纳总结,以形成知识体系.

(作者单位：河北省滦平县职教中心)