组合数的多重“身份”
2016-03-11王雪芹,高雪松

◇北京王雪芹(特级教师)高雪松
1身兼数“职”平常事
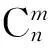
应当说,数学中普遍存在这种“身兼数职”的现象,其意义既很微妙(值得耐心体味),又很重大(值得深入研究).
2“组合数”关乎大局
1) 组合数应用之一——可以简单证明“二项式定理”.按定义
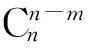
①
你看,不费“吹灰之力”,就证明了二项式定理,比用数学归纳法证明要简单得多.
此法还可推广使用于求(x+a1)(x+a2)…(x+an)的展开式,如求(x+2/x-2)5展开式中常数项:

用上述方法很容易求出展开式常数项是

2) 推动“组合数学”学科的建立.组合数学是研究离散对象的排布、配置、选取、分类、组织与结合等的数学学科,中国古代研究的九宫、八卦、干支计数等,都属于组合数学.贾宪-杨辉三角及相关恒等式的研究,流行的游戏与博弈,如围棋、中国象棋、国际象棋、麻将、扑克、桥牌等,都与组合数学有关.
组合数学关心的是,事物按某种规则的安排,这种安排的存在性、构造、计数和分类等.组合数学自诞生以来,已积累了大量优异的模型、原理、典型方法和技巧,如加法原理、乘法原理、容斥原理,线排列模型、环形排列模型,递推方法以这些优异的成果来反哺数学.
3) 通过对组合数学丰硕成果的分析,获得了若干典型的、规律性的认识,并用以对整个数学的概念、法则、公式、命题等,进行规律化处理,事实上.无论是数学概念的定义,法则的应用,还是命题的证明,无处不贯串着组合因素(顺序和结构以及顺序结构的变化时,那种保持不变的东西).为深刻理解,正确掌握数学的内容和方法,就要着意抓住和厘清其中的组合因素.这种着意发现、抓住数学内容中组合因素的思想,力求抓住数学问题中,当结构和顺序变化时,不变的因素(在纷繁的情况中一致因素)的思想方法,就是组合思想.
有了组合思想就能看穿全局、把握全局,因此,组合思想是一种全局性的思想,是从数学本身中概括出来的学习、研究、应用、教学数学的一种战略思想.
3与多项式联姻
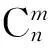
1) 展开式系数结构的组合特征
②
这就为二项式定理带来更多的证法.笔者搜集到一些,供大家研究.

③

④
由式③+④得

当x≠-1时,{Sn}为等比数列,首项S1=1+x,公比q=1+x,从而
Sn=(1+x)(1+x)n-1=(1+x)n.
当x=-1时,可直接验证:Sn=0=(1+x)n.
综上可得
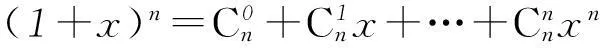
⑤
令x=b/a,代入式⑤得
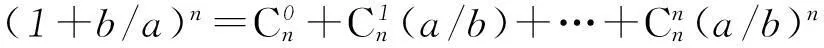
两边同乘以bn得
(a+b)n=an(1+x)n=anSn=

这就是式①.
证法2(拆项法)这是与证法1过程相反的方法:



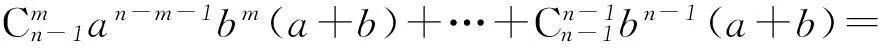



证法3(微分法)设f(x)=(x+b)n,展开式为
f(x)=a0xn+a1xn-1b+…+
amxn-mbm+…+an-1xbn-1+anbn,
微分,得
f′(x)=n(x+b)n-1=na0xn-1+(n-1)a1xn-2b+…+
(n-m)amxn-m-1bm+an-1bn-1,…,f(n-m)(x)=
n(n-1)…(m+1)a0xm+…+(n-m)…
2am-1xbm-1+(n-m)!ambm.
在f(x),f′(x),…,f(n-m)(x)中,令x=0,得
bn=anbn,nbn-1=an-1bn-1,…,
n(n-1)…(m+1)bm=(n-m)!ambm,
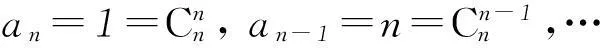

按组合公式即知

此法的好处在于顺带得出了am的计算公式.
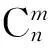

取a=1,b=-1,得

类似地,还可导出很多.
4从贾宪到华罗庚
我们今天所说的“杨辉三角”出自1261年杨辉著的《详解九章算法》,名字是“开方作法本源图”,自注称“出于《释锁》算书,贾宪用此术”.其中只到第7行:1,6,15,20,15,6,1.后朱世杰《四元玉鉴》(1303年)有“古法七乗方图”者,写到第9行,即(a+b)8展开式的系数.不像我们今天,写几行后,就用“…”表示可继续到任意行.此图在贾宪那里,是用来“开方”的,而朱世杰则用来做“乘方”.
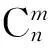
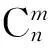
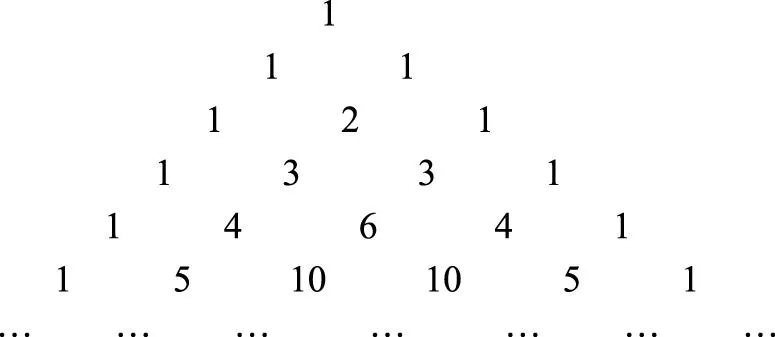
图1
2) 它形象、直观、优美,初步的规律显而易见,深入观察,则可发现一些更深刻的规律.因此,它体现数学美,数学观察、类比、发现、这些合情推理的思想.
4) “杨辉三角”有独立的研究价值.
如数学大师华罗庚著《从杨辉三角谈起》一书,除了讲“杨辉三角的基本性质”和“二项式定理”之外,还讨论了“杨辉三角的一些应用”.这些应用项目有:开方,高阶等差级数,差分多项式,逐差法,堆积术,混合级数,无穷混合级数,循环级数(包括斐波纳契级数),倒数级数和反平方级数等.由于讲得深入浅出,高中同学都能看懂,但现在多已“打进”了高等数学领域.
笔者大力倡导“初等数学研究”并在《数阵及其应用》一书(哈尔滨工业大学出版社,2012年)中,深入地研究了杨辉数阵(由杨辉三角旋转而成)

其斜通项为
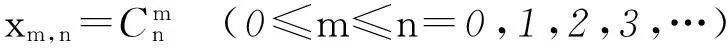
而它的直通项(第i行的第j个数)为
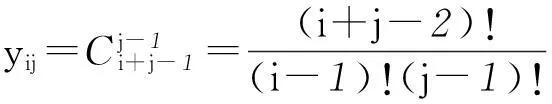
它有非常丰富的性质,如它是个对称数阵:yij=yji,第i行是(i-1)阶等差数列等.
(作者单位:北京师范大学第二附属中学)
