海工混凝土氯离子分布概率模型分析与应用

高　远，陆春华，袁思奇，陈素碧，杨金木

(江苏大学土木工程与力学学院，江苏镇江　212013)



海工混凝土氯离子分布概率模型分析与应用

高远，陆春华，袁思奇，陈素碧，杨金木

(江苏大学土木工程与力学学院，江苏镇江212013)

摘要：在海工混凝土结构中，由于氯离子侵蚀导致的钢筋锈蚀问题十分普遍。为准确判断钢筋初锈时间，预测结构耐久性劣化规律，在现有氯离子扩散模型的基础上，基于蒙特卡罗理论，利用MATLAB软件对钢筋周围氯离子浓度分布进行随机抽样模拟。结果表明一定时间段内(10年、50年、100年)钢筋周围氯离子浓度服从对数正态分布，并提出判断钢筋锈蚀的概率模型，以概率方法判断钢筋锈蚀，其可靠性将大大增加。结合该模型对连云港港区现场服役混凝土构件进行了氯离子含量预测，现场取粉试验结果基本符合该模型分布，其均值吻合较好，并对港区混凝土结构耐久性使用寿命失效概率进行了风险评估。

关键词：蒙特卡罗法; 钢筋初锈; 氯离子浓度分布; 概率模型

氯盐环境下钢筋锈蚀是引起结构耐久性问题的主要原因。氯离子侵入导致钢筋锈蚀的过程主要是通过混凝土保护层到达钢筋表面，破坏其表面钝化膜，导致钢筋局部锈蚀，在腐蚀电池作用下，锈蚀不断发展。在此过程中氯离子对钢筋锈蚀具有催化作用。因此，可将钢筋初锈视为结构耐久性退化演变的起始点。实际工程中正确判断钢筋初锈时间是准确预测结构耐久性寿命的重要依据之一。而传统判断钢筋锈蚀的方法主要采用电化学检测法，包括自然电位法、交流阻抗技术和极化测量技术等[1]。其中自然电位法即半电池电位法应用最为广泛。电化学方法以其测试的速度快、灵敏度高、可连续跟踪和原位测试的优点,成为目前比较成熟的测试方法[2-3]。但此类方法的缺点是易受外界因素干扰，且判断可靠性不高。因此，许多国内外学者采用理论分析的方法确定钢筋初锈时间，并提出相应计算模型。如D. V. Val[4]将侵蚀过程简化为扩散过程，没有考虑对流、温湿度对氯离子扩散系数的影响，利用Fick第二定律得到钢筋初锈时间的计算公式；S. Morinaga[5]基于现场与实验室快速试验数据提出了一个预测从初锈到锈胀开裂时间的经验公式。而此类方法的计算模型中一般没有考虑材料、环境等影响因素的不确定性，以定值(一般取变量平均值或相关规范中的标准值或经验值)进行计算，所得结果离散性较大。

基于以上考虑，本文在以往理论计算模型基础上，考虑各影响因素的不确定性，提出判断钢筋锈蚀的概率模型。结合蒙特卡罗基本思想，利用MATLAB软件对钢筋周围氯离子浓度分布进行模拟，以预测各时间段钢筋锈蚀的概率。并利用该模型对连云港港区现场服役混凝土构件进行了氯离子含量的预测，对比现场取粉试验结果以验证模型准确性。

1理论模型分析

氯离子对钢筋表面钝化膜具有极强的去钝化作用，可导致钢筋发生局部锈蚀[6]。1970年意大利的Callepari首次提出，在假定混凝土材料各向均质同性、氯离子不与混凝土发生反应的条件下,氯离子在混凝土中的扩散行为可用Fick定律[7-9]来描述：

(1)

式中：C为氯离子浓度，以氯离子质量占胶凝材料质量百分比表示(%)；x为距混凝土表面距离(mm);t为暴露时间(s);D(t)为氯离子扩散系数(mm2/s)。

当混凝土结构处于完全饱和状态时氯离子在混凝土中的输运方式以扩散为主，而在非饱和状态下，混凝土表面一定深度存在对流区，对流区以内仍可视为扩散的方式。因此本文为简化运算仍将氯离子侵蚀过程视为以扩散方式为主，同时考虑温度、湿度、应力等影响因素。其氯离子扩散系数可表示为[10]：

(2)

式中:tref为相对时间(s)，一般取混凝土养护28 d龄期；Dref为相对时间对应的氯离子扩散系数(mm2/s)；KT，KR，Kσ分别表示温度、湿度、应力的影响系数，参考文献[11-13]按以下计算公式进行计算：

KT=exp[0.028(T-23)]，T>0

(3)

(4)

(5)

式中:T为温度(℃)；R为湿度(%)；σc/t/fck/tk为预应力水平；λ为经验系数，一般拉应力水平下取为0.25，压应力时取-0.20。

若假定混凝土内初始浓度为零时，结合式(2)～(5)，由式(1)可得混凝土内部氯离子浓度随深度的变化规律模型为：

(6)

式中:Cs为表面氯离子浓度(%)；m为时间衰减系数，与混凝土质量有关，按m=2.5×w/c-0.6计算[14]，其中w/c为混凝土水灰比。因此，若已知各随机变量的分布规律和参量，可弄清混凝土内氯离子浓度的分布规律与参量。

设氯离子临界浓度值为Ccr，本文按氯离子含量占胶凝材料百分比表示。当以钢筋锈蚀为目标条件时，其功能函数可表示为：

(7)

(8)

因此，若已知各随机变量的分布规律与参量，可弄清混凝土内氯离子浓度的分布规律与参量。而在氯离子浓度概率密度函数已知的情况下可确定某一时间钢筋锈蚀的概率大小。

2基于可靠度理论的氯离子浓度分布及钢筋锈蚀研究

实际上，氯离子侵蚀致使钢筋锈蚀是一个漫长而复杂的过程。而按照上述计算公式将模型中各影响因素取为定值，所求的氯离子浓度值以及相应的钢筋初锈时间均为确定的值，其可靠度仅为50%。而实际工程环境中混凝土材料、养护过程、运营环境等影响因素都具有很大的不确定性。因此，本文利用概率的方法分析了钢筋周围氯离子浓度的变化规律，以预测钢筋锈蚀的概率。

2.1相关变量参数的选取

目前，许多国内外学者在大量试验数据和检测结果基础上，考虑材料和环境变量存在显著的不确定性，确定了模型中各随机变量的统计参数。海港工程的相关规范给出了锈蚀模型中参量的标准值及最低耐久性要求，包括大气区、浪溅区、水位变动区不同区域表面氯离子浓度、氯离子临界浓度等最低要求。本文在已有研究成果的基础上，选取主要影响参数的分布情况如表1所示。

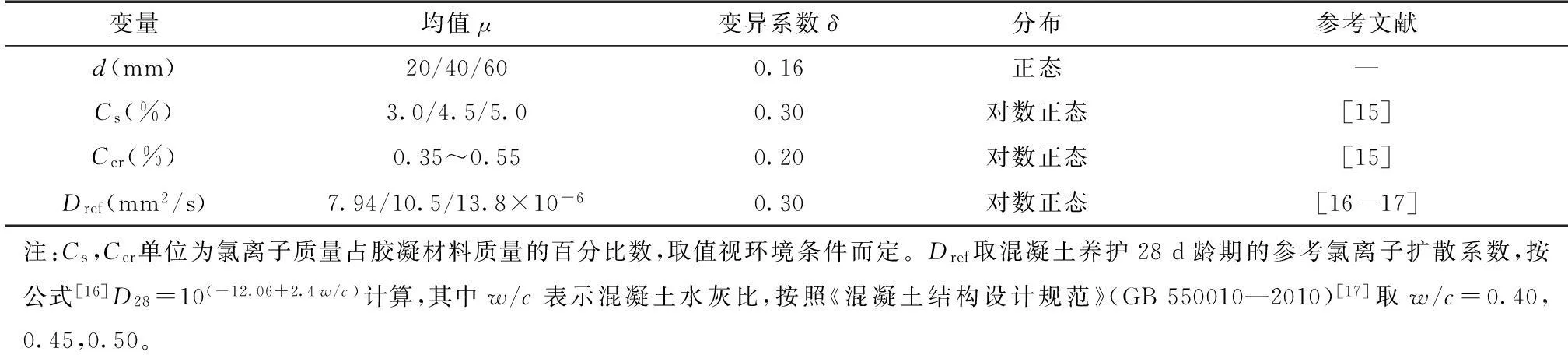
表1　主要随机变量参数统计

2.2钢筋周围氯离子浓度概率分布

蒙特卡罗法采用统计抽样理论近似求解数学问题或物理问题[18]。基于这一随机抽样模拟的思想，本文采用MATLAB软件对上述理论模型进行了N次(本文采用N=105)随机统计抽样，分别对10年，50年，100年氯离子侵蚀至钢筋周围浓度分布进行模拟，得到钢筋周围氯离子浓度统计分布直方图及其核密度图，并利用MATLAB工具箱进行拟合，发现氯离子浓度的分布规律可近似利用对数正态分布LN(μ，σ2)来描述。如图1所示，分别为10年、50年、100年氯离子浓度概率密度曲线图。

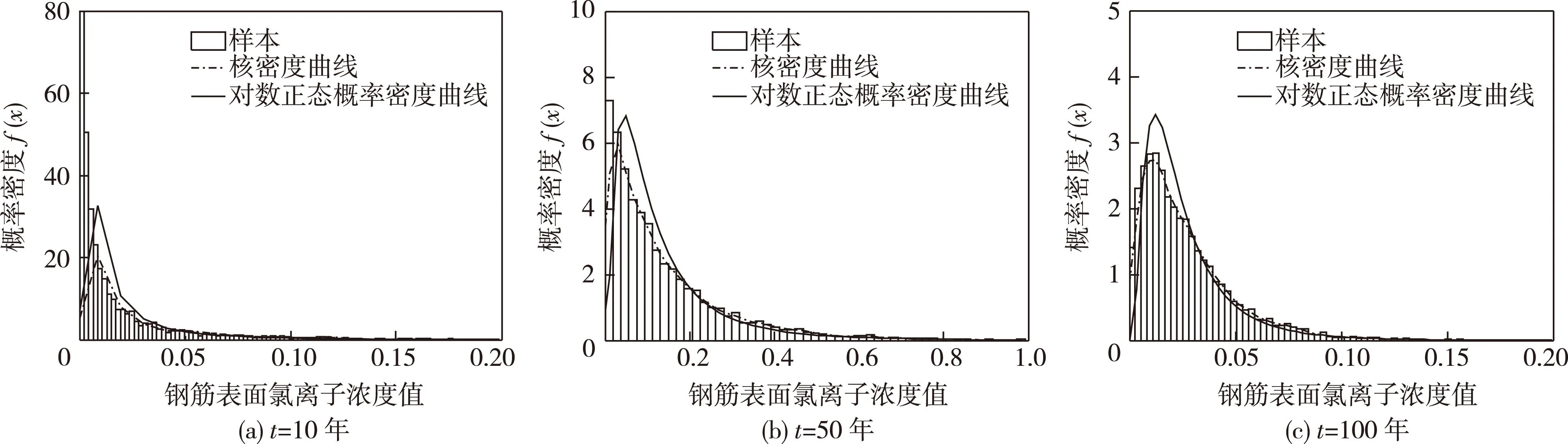
图1　钢筋表面氯离子浓度拟合对数正态分布Fig.1　Fitting logarithmic normal distribution of chloride ion concentration on steel surface

为进一步验证模型的正确性，需对模型进行检验。而在概率统计理论中，χ2检验作为检验直方图与拟合密度函数之间差异是否显著的方法，特别适用于大样本情况。因此，本文采用χ2检验，假设H0：钢筋周围氯离子浓度服从对数正态分布，利用下述关系式作为检验假设H0的统计量[19]：

(9)

于是，经n次抽样分析，并计算χ2统计量结果，在置信水平α(α=0.05)下，可满足下式，则接受H0，即钢筋周围氯离子浓度服从对数正态分布。

χ2≤χ∂2(k-r-1)

(10)

2.3影响因素分析

2.3.1保护层厚度取如下计算参数：tref=28 d，w/c=0.40，Dref=7.94×10-6mm2/s，R=75%,m=0.4，Cs=3%，Ccr=0.55%。根据式(8)给出的锈蚀概率模型，利用MATLAB软件进行N次随机抽样模拟。得到不同保护层厚度对钢筋周围氯离子浓度及钢筋锈蚀的影响如图2所示，从图中可以看出，随着保护层厚度的增大，钢筋周围氯离子浓度快速减少，同时钢筋锈蚀的概率显著降低。因此，增大保护层厚度可延缓钢筋腐蚀，有利于提高结构耐久性寿命。

图2　不同保护层厚度氯离子浓度、钢筋锈蚀概率随时间变化规律Fig.2　Variation of chloride ion concentration and reinforcement corrosion probability for different thicknesses with time

2.3.2表面氯离子浓度由于不同区域结构接触氯盐方式不同，表面氯离子浓度存在差异。取如下计算参数：tref=28 d，w/c=0.40，Dref=7.94×10-6mm2/s，R=75%,m=0.4，d=40 mm，大气区与水位变动区Ccr=0.55%，浪溅区Ccr=0.4%。如图3所示，当表面氯离子浓度分别为3%(大气区)、4.5%(浪溅区)、5%(水位变动区)时钢筋周围氯离子浓度均值与钢筋锈蚀概率随时间显著增长，并以浪溅区结构侵蚀最为严重，这是由于该区域侵蚀介质与氧气充足，致使钢筋锈蚀概率显著增加。

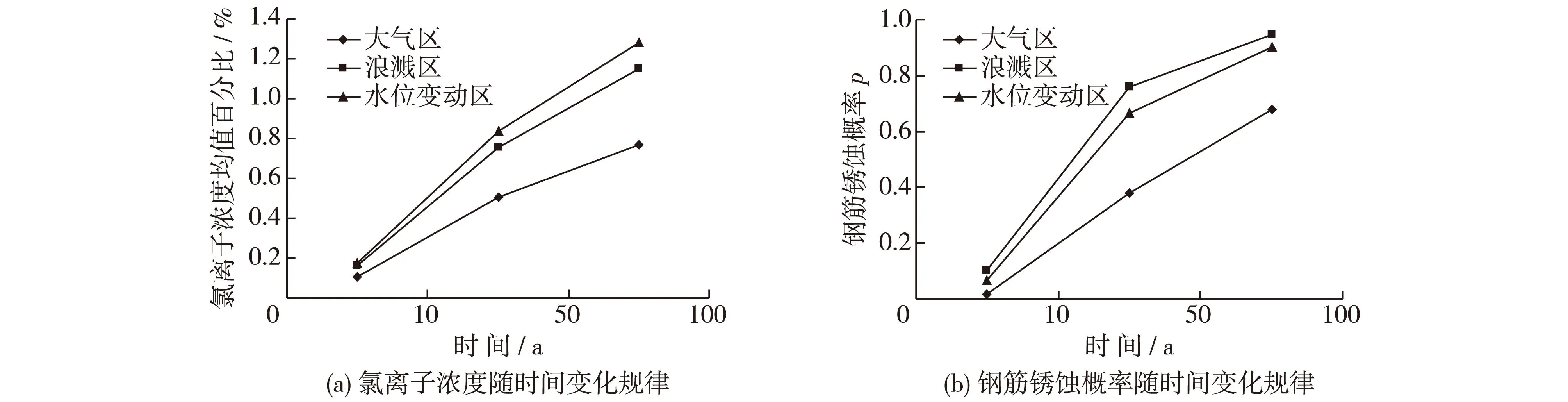
图3　不同区域氯离子浓度均值、钢筋锈蚀概率随时间变化规律Fig.3　Variation of chloride ion concentration and reinforcement corrosion probability for different exposure conditions with time

2.3.3混凝土质量取如下计算参数：tref=28 d，R=75%，m=0.4，Cs=3%，Ccr=0.55%，根据混凝土材料的耐久性基本要求，分别取水灰比w/c=0.40，0.45，0.50。图4给出不同水灰比混凝土内氯离子浓度与钢筋锈蚀概率随时间增长的曲线。从图4可见，水灰比从0.40增大到0.50，钢筋锈蚀显著增加。这是由于混凝土水灰比越大，抗渗性越差，氯离子扩散系数越大，混凝土结构耐久性越差。因此，合理控制混凝土水灰比有利于提高结构耐久性寿命。

图4　不同水灰比的氯离子浓度均值、钢筋锈蚀概率随时间变化规律Fig.4　Variation of chloride ion concentration and reinforcement corrosion probability for different water cement ratio with time

3现场试验对比分析

3.1现场耐久性试验设计

图5　t=40年氯离子浓度拟合对数正态分布Fig.5　Fitting logarithmic normal distribution of chloride 　ion concentration for 40 years

2013年4月对连云港港区一些泊位的海工混凝土结构进行耐久性检测。其中3～4号泊位位于连云港港区东部的二号突堤东侧，1974年建成，结构形式为高桩梁板式，设计为一个5 000 t级泊位和一个1万t级泊位，总长322 m，宽26.37 m，其中码头宽13.00 m，平台宽13.37 m。排架间距6 m。本次试验主要侧重于混凝土结构中氯离子含量的测定。分别对海洋环境中典型的3个侵蚀区域(大气区、浪溅区、水位变动区)钻孔取粉，采用冲击钻每隔5 mm取一次粉样。对各测点取粉完毕后利用RCT快速氯离子含量测试仪对所取粉样进行氯离子浓度测定。

3.2现场试验结果与模型对比分析及风险评估

根据现场试验环境调查，近50年内连云港港区年平均温度为14 ℃，湿度为80%。利用上述随机模拟方法对该区混凝土结构中氯离子浓度分布进行模拟。得到服役期近40年的混凝土结构，深度20，40和50 mm处氯离子浓度分别近似服从LN(-0.866 7，0.326 1)，LN(-1.394 2，0.483 5)，LN(-1.909 3，0.637 3)的对数正态分布，如图5所示。

现场取样试验，其10个测点a～j的测定结果，及利用模型模拟氯离子浓度均值结果如表2所示。现场取粉试验结果基本服从模型拟合分布，其均值与模型拟合结果吻合较好。说明该模型可较好地预测混凝土中氯离子浓度的分布。因此可利用该模型预测海工混凝土结构中氯离子的侵蚀程度，以此作为评估结构耐久性失效风险的依据。

表2　连云港取粉试验结果与模型计算氯离子浓度均值

图6　运营期混凝土结构的使用寿命Fig.6　Service life of concrete structures

运营期混凝土结构的使用寿命一般分为 4个阶段，如图6所示。对于海工重大混凝土结构，一般采用t0作为耐久寿命的终结。因此，可利用该模型对以钢筋脱钝为极限状态设计要求的重大海工结构进行耐久性寿命的概率风险评估与预测。以上述连云港区混凝土结构为例，混凝土为C40，以钢筋脱钝为结构设计使用寿命极限状态，对该区混凝土结构耐久性失效风险进行概率评估发现，当结构服役80年失效概率达0.610 5；服役100年后失效概率达0.825 5；预测结构在服役近120年后，失效概率达0.9以上。因此，在结构服役近100年后就需要对结构采取维修加固措施。

4结语

(1)对海洋环境下钢筋混凝土结构，在已有学者研究氯离子扩散模型基础上，建立了氯离子侵蚀导致钢筋锈蚀的概率模型。可大大提高判断钢筋锈蚀的可靠性。

(2)基于蒙特卡罗理论，借助MATLAB对钢筋周围氯离子浓度分布规律进行抽样模拟，发现某一时间段(本文取10年、50年、100年)，一定深度处(本文取保护层厚度20，40，50和60 mm)的氯离子浓度分布近似服从对数正态分布。

(3)对影响钢筋初锈的各主要因素计算分析表明，增大保护层厚度，合理控制混凝土水灰比可降低钢筋锈蚀概率，有利于提高结构耐久性寿命。同时根据上述概率模型预测了连云港港区现场服役构件内氯离子含量。现场取粉试验样本点基本服从该模型分布，其均值吻合较好。因此可利用该模型预测混凝土内氯离子侵蚀情况，评估结构耐久性使用寿命。

参考文献：

[1]罗刚, 施养抗. 钢筋混凝土构件中钢筋锈蚀量的无损检测[J]. 福建建筑, 2002(4): 55- 57. (LUO Gang，SHI Yang-kang. Review of non-destructive methods in assessment corrosion in reinforced concrete member[J]. Fujian Construction, 2002(4): 55- 57. (in Chinese))

[2]朱雅仙, 朱锡昶, 葛燕, 等. 用半电池电位评估钢筋混凝土构件中钢筋腐蚀状态[J]. 水利水运工程学报, 2003(4): 41- 44. (ZHU Ya-xian，ZHU Xi-chang, GE Yan, et al. Evaluation of reinforcement corrosion in reinforced concrete member by half-cell potential method[J]. Hydro-Science and Engineering, 2003(4): 41- 44. (in Chinese))

[3]王元战, 黄东旭, 王军. 考虑荷载影响的钢筋混凝土构件钢筋锈蚀模型[J]. 水道港口, 2011, 32(3)： 202- 205. (WANG Yuan-zhan, HUANG Dong-xu, WANG Jun. Reinforcing bar corrosion model of RC member considering load effect[J]. Journal of Waterway and Harbor, 2011, 32(3): 202- 205. (in Chinese))

[4]VAL D V. Factors affecting life-cycle cost analysis of RC structures in chloride contaminated enviroments[J]. Journal of Infrastructure Systems, 2007, 13(2): 135- 143.

[5]MORINAGA S. Prediction of service lives of reinforced concrete buildings based on rate of corrosion of reinforcing steel[R]. Tokyo: Shimizu Corp, 1998: 82.

[6]邓春林, 王胜年, 余其俊. 几种钢筋锈蚀的电化学检测技术的对比研究[J]. 华南港工, 2008(2): 45- 50. (DENG Chun-lin, WANG Sheng-nian, YU Qi-jun. Research of electrochemical test methods for detecting the corrosion states of reinforcing steels in concrete[J]. South China Harbour Engineering, 2008(2): 45- 50. (in Chinese))

[7]赵羽习, 金伟良. 钢筋锈蚀导致混凝土构件保护层胀裂的全过程分析[J]. 水利学报, 2005, 36(8): 939- 945. (ZHAO Yu-xi, JIN Wei-liang. Analysis of the cracking of concrete cover due to rebar corrosion[J]. Journal of Hydraulic Engineering, 2005, 36(8): 939- 945. (in Chinese))

[8]COLLEPARDI M, MARCLALISA, TURRIZIANI R, et al. Penetration of chloride ions into cement pastes and concrete[M]. Ohio: American Ceramic Society, 1972.

[9]RICHARDSON M G. Fundamentals of durable reinforced concrete[M]. Taylor & Francis, 2002.

[10]LU Chun-hua, JIN Wei-liang, LIU Rong-gui. Probabilistic lifetime assessment of marine reinforced concrete with steel corrosion and cover cracking[J]. China Ocean Eng, 2011, 25(2): 305- 318.

[11]ABABNEH A, BENBOUDJEMA F, XI Y. Chloride penetration in nonsaturated concrete[J]. Journal of Materials in Civil Engineering, 2003, 15(2): 183- 191.

[12]SAMSON E, MARCHAND J. Modelling the effect of temperature on ionic transport in cementitious materials[J]. Cement and Concrete Research, 2007, 37(3): 455- 468.

[13]LU C H, WANG H L, JIN W L. Modeling the influence of stress level on chloride transport in prestressed concrete[C]∥International Conference on Durability of Concrete Structures, 2008: 26- 27, 239- 245.

[14]MANGAT P S, MOLLOY B T. Prediction of long term chloride concentration in concrete[J]. Materials and Structures, 1994, 27(7): 338- 346.

[15]JTJ 275—2000海港工程混凝土结构防腐蚀技术规范[S]. (JTJ 275—2000Corrosion prevention technical specifications for concrete structures of marine harbour engineering[S]. (in Chinese))

[16]BENTZ E C, THMAS M D A. Life-365 service life prediction model:computer program for predieting the service life and life-cycle costs of reinforced conerete exposed to chlorlde[R]. SFA: Life 365 Manual, 2001.

[17]GB 50010—2010 混凝土结构设计规范[S]. (GB 50010—2010Code for design of concrete structures[S]. (in Chinese))

[18]张键仁, 刘扬, 许福友, 等. 结构可靠度理论及其在桥梁工程中的应用[M]. 人民交通出版社, 2002: 20- 34. (ZHANG Jian-ren, LIU Yang, XU Fu-you, et al. Structural reliability theory and application in bridge engineering[M]. China Communication Press, 2002: 20- 34. (in Chinese))

[19]庄楚强, 何春雄. 应用数理统计基础[M]. 4版. 广州： 华南理工出版社, 2013: 150- 156. (ZHUANG Chu-qiang, HE Chun-xiong. Application of mathematical statistics[M]. 4th ed. Guangzhou: South China Science and Technology Press, 2013: 150- 156. (in Chinese))

Application analysis of probability model for chloride ion erosion distribution in marine concrete structure

GAO Yuan， LU Chun-hua， YUAN Si-qi， CHEN Su-bi， YANG Jin-mu

(FacultyofCivilEngineeringandMechanics,JiangsuUniversity,Zhenjiang212013,China)

Abstract：As for the durability of the concrete structure, the problems of steel corrosion caused by chloride ion erosion are common in the marine works. In order to accurately forecast and predict reinforcement corrosion and structure durability degradation law, the basic idea of Monte Carlo is used, combined with MATLAB toolbox to simulate the chloride ion concentration distribution around the surrounding reinforement bar. The analysis results show that in a certain period of time (10 a, 50 a, 100 a) the chloride ion concentration around reinforced bar obeys the lognormal distribution. The probability model of chloride ion diffusion is established. Judging the reinforcement corrosion by a probability method, the accuracy can be greatly increased. At the same time, the probability model is used to predict the concrete structure durability of the Lianyungang port service components, and the results are in conformity with those of the field tests. And the risk assessment is made for the failure probability of the concrete structure service life. Therefore, this model can provide a theoretical basis for the nondestructive testing of the chloride ions content in concrete and for the judgment of steel-bar corrosion in the marine concrete works.

Key words：Monte Carlo method; corrosion initiation; chloride ion concentration profile; probability model

中图分类号：TU528

文献标志码：A

文章编号：1009-640X(2016)01-0037-07

作者简介：高远(1990—)， 女， 吉林吉林人, 硕士研究生， 主要从事混凝土结构耐久性研究。

基金项目：国家自然科学基金资助项目(51278230, 51378241); 教育部博士点基金资助项目(20123227110006); 江苏大学高级人才科研基金资助项目(11JDG132)

收稿日期：2015-04-28

DOI:10.16198/j.cnki.1009-640X.2016.01.006

高远， 陆春华， 袁思奇， 等. 海工混凝土氯离子分布概率模型分析与应用[J]. 水利水运工程学报, 2016(1): 37-43. (GAO Yuan, LU Chun-hua, YUAN Si-qi, et al. Application analysis of probability model for chloride ion erosion distribution in marine concrete structure[J]. Hydro-Science and Engineering, 2016(1): 37-43.)

E-mail：chuckxmu@foxmail.com