分析如何在高中数学教学中渗透数形结合思想

◆张晓光

(吉林省双辽市第二中学)

分析如何在高中数学教学中渗透数形结合思想

◆张晓光

(吉林省双辽市第二中学)

随着新课程标准的进一步实施，越来越多的教师开始认识到学生的主体地位。在高中数学教学中，教师进一步要求学生把握数学基本概念，灵活运用数学基本思想，特别是数形结合的思想。由于学生对于数形结合思想的理解不够，高中数学教师要在教学实践中有意识的引导和培养学生使用数形结合思想。通过对数形结合思想概念内容的分析，阐述如何在高中数学教学中渗透数形结合思想。

高中数学 数形结合 策略

一、数形结合思想

在数学中，数与形是最古老、最基本的两个研究对象，它们在一定的条件下可以相互转化。在具体的数学教学中，数与形相互联系，这样的联系就称为数形结合。数形结合作为一种数学思维方法，大致分为两种情况：一是借助于数的精确性来阐明形的某些属性，即“以数解形”；二是借助形的几何直观性来阐明数之间的某种关系，即“以形助数”。

在高中数学教学中，运用数形结合的思想，可以解决集合、三角函数、抛物线、方程与不等式等多种问题，是学生解题的优质工具，也是教师授课的必选途径。不管是形转数，还是数助形，只有在实践中才能更好的把握和理解数形结合的思想。

二、在数学教学中渗透数形结合思想的具体策略

(一)利用数形结合思想讲授基本概念。高中数学教师在讲授基本的数学概念时，尽量使用数形结合的思想和方式，向学生直观的演示概念的推算过程，让学生真正理解和把握某一数学概念，并能够实际运用到以后的解题过程中。

例如，在关于集合这一概念的课程中，教师可以通过图形的方式在来进行讲解。如下图，用大小两个圆圈的不同位置关系，来表示集合中的四个基本概念。

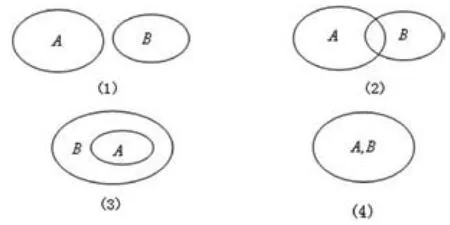
如上图所示，(1)中两个圆圈没有公共相交的部分，即集合A和集合B没有共同的元素，(2)中两个圆圈有相交的部分，即集合A和集合B有共同的元素；(3)中集合A包含于集合B中，说明集合A属于集合B；(4)中集合A与集合B完全重合，即集合A=B。根据(3)(4)的情况又可以引申出真子集和子集的概念，即如果集合A中的元素都是集合B中的元素，但是结合B中存在元素不属于集合A ,则集合A是集合B的子集；如果集合A中的元素都是集合B中的元素，但是集合A不等于集合B,则集合A是集合B的真子集。让学生充分从字面上理解交、并、补的概念。在学习好基本概念的基础上，教师还要鼓励学生用数学语言来表示具体的概念。如，AUB(交)，A∩B(并)，A?B(包含于)，元素X∈B(属于)等，以便学生在以后的解题过程中可以灵活便捷使用好集合概念解决疑难问题。

(二)利用数形结合思想解决疑难问题。在高中数学教学中，除了在数学概念的教学中要渗透数形结合的概念，更主要的是教师要使用数形结合的概念帮助学生解决疑难问题，将复杂的题目换化成简单直观的数学图形，这样不仅可以节省学生的解题时间，也能够提高学生解题的正确率。

例如，设方程|x2-1|=k+1，试讨论k取不同范围的值时其不同解的个数的情况。首先这是一个方程问题，可以把等式两边的式子转化成两个函数，即 y2= | x2- 1 |、 y2= k + 1，并作图查看两个函交点的个数来判断K的取值范围，进而进一步解题。由于 y2= k + 1表示平行于X轴的所有直线，于是通过对下图的直观观察，可以得到以下的结论：

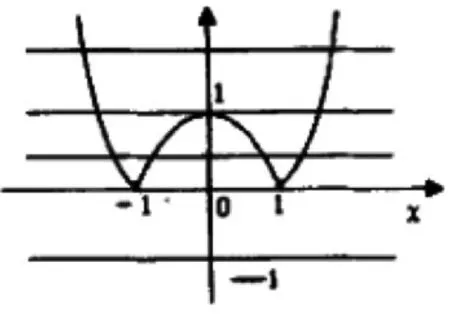
当k<-1时，两个函数没有交点，也就表示原方程没有解；当k=-1时，两个函数有两个交点，也就表示原方程有两个解；当-10时，两个函数有两个交点，也就表示原方程有两个解。

(三)适当布置具有数形结合思想的练习题。高中数学教师在除了教学过程中有意识渗透数形结合的解题思路外，还需要有针对性的为学生布置适当的数形结合题型的练习题，让学生加强训练，熟能生巧，才能够在以后的考试中准确判断哪些题是可以使用数形结合的思想，并能够准确作图，灵活转换。

[1]刘桂玲.数形结合思想方法在高中数学教学中的应用分析[J].中国校外教育,2015,(13):106.

[2]冉正伟.浅谈在高中数学教学中如何渗透数形结合思想[J].科学咨询,2012,(06):141.