见题识方，借图寻法

陈艳

[摘要]应用题是小学数学教学中的重点，也是学生学习的难点.学生应用题学习效果不理想的影响因素有许多，但其根源是学生审题能力的缺失.本文正是基于此，就如何培养学生审题能力进行探析，并从识别关键信息，借助有效图式，利用逆向反证三个维度作具体阐释.

[关键词]小学数学；应用题；审题能办

应用题在小学数学教学中占据着举足轻重的地位，一方面应用题能够将抽象的数学概念以凝练的语句转化成具象的生活应用情境，这对于训练、培育学生数学应用能力是大有裨益的；另一方面应用题有着十分丰富的组合和呈现形式，所有的知识点都可以进行联结整合到应用题中，这使得应用题作为教师的“杀手锏”，已成为考察学生知识学习情况和综合应用能力的重要手段，应用题如此重要，自然成为小学数学教学的“兵家必争之地”，教师都铆足了劲来进行应用题教学，做了不少努力，到最后却发现，应用题竟成了学生“最易掉链子”的部分.

应用题真的这么难吗？笔者不以为然，学生听完教师的解析后，往往表示好理解，并不难；但当教师对题目稍加变化再呈现给他们的时候，学生似乎又卡壳了.究竟是什么导致学生的应用题练习“久治不愈”呢？笔者以为“病症”的根源在审题.审题是应用题解题的根本与前提，审题质量直接决定做题的速度与正确率.正是因为审题不得要领，所以学生在应用题学习过程中问题频出，“症状反复”，难以举一反三.因此，要学好应用题，学生审题能力的培养十分重要，而这部分恰恰是教师最容易忽视的（大部分教师都把精力放在解题过程的讲解上）.基于此，笔者就如何有效引导学生进行应用题审题，高效做题进行策略探析，总结出如下三点经验：

识别关键信息，判定审题方向

审题的第一步是读题，通过有效阅读题目，能够最大限度掌握题目信息，明确解题方向，为下一步审题奠定基础.许多教师不重视引导学生读题，这是错误的，学生在解答应用题时出现的很多错误，其实就是因为读题没读好造成的.例如有这样一道应用题：“一瓶洗衣液要18元，一瓶洗洁精要10元，请问两袋洗衣液和一瓶洗洁精一共多少钱？”有学生就答成：“18+10=28.”为什么会答错？就是因为读题的时候没看清楚条件，把“两袋洗衣液”中的“两”字给看漏了.所以准确有效的读题十分重要.

那该如何指导学生读题，有效培养学生的读题能力，让学生能够通过读题有效锁定题目中的关键信息，有力促进学生审题、答题呢？答案很简单，那就是抓住关键信息，一般来说，学生只要能够有效抓取两类关键信息，有效读题就将不再是什么问题.第一类关键信息是数字，数学是由数字组成的，数字自然是数学解题的钥匙，抓取题目中的全部数字，对于有效解题有着不言而喻的促进作用；不过在应用题中并不是所有数字都是一目了然的，有些数字隐藏在条件中，需要教师多通过引导，让学生能够有效破译，找出隐藏数字.例如这样一道题目：“开学第一天起，小红每天都会写一篇日记，现在她已经写了42篇日记了，请问开学几个礼拜了？”这道题目学生通过读题都能够快速找出“42”这个数字，但只有一个数字显然无法解题，这个时候许多学生就卡壳了，这时教师就要引导学生找出隐藏条件“一个礼拜有7天”，找出隐藏在条件里的数字，题目就迎刃而解了.第二类关键信息是关键词，应用题中的关键词与数字一同组成了解答题目的全部要件，抓取关键词对于解题意义重大，那么有哪些词语称得上关键词呢？例如表明数字关系的词语：和差、倍数、多少、占比等；例如表明运算联系的词语：速度和时间是路程关系，工作效率和时间是工程关系等；又例如一些连接词：总共、各有、其中等.通过指导学生利用读题抓取这些关键词，将有助于学生准确把握各个条件之间的关系，帮助学生准确判定审题方向.

借助有效图式，分析解题策略

审题的第二步就是对读题所获取的条件进行分析，制定解题策略.这一步可以说是审题的关键，如果说读题是为解题做好物质准备的话，那么分析就是为解题做好战术规划，审题分析没做好，解题必然走向错误的方向，导致失分，例如在进行应用题“某果园要向外运输45吨苹果，用一辆载重2.5吨的货车运了9次后，如果改用载重1.5吨的货车运，还要运多少次？”一名做错的学生是这样答的：“45÷1.5=30（次）.”这道题目学生为什么会做错？就是因为没有做好审题分析，题目要求的是“2.5吨货车运完9次后，1.5吨货车还需要运几次”，该生理解成“改用1.5吨货车需要运几次”，题目分析过程中，失之毫厘谬以千里，所以做好题目分析，十分重要.

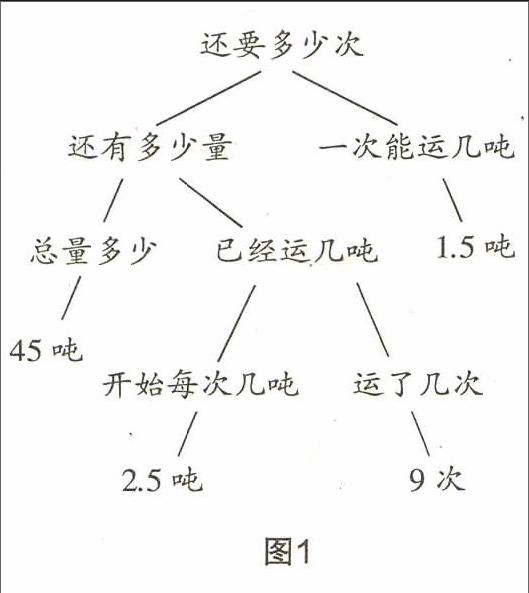
既然题目分析如此重要，那有什么有效的策略可以用来指导学生进行题目分析呢？笔者认为可以借助图式.皮亚杰的认知发展理论已经点明了学生的思维世界是以具象思维为主的，所以要指导学生更为高效、准确地分析题目，通过图式来使抽象的解题逻辑具象化，不是“正中下怀”吗？笔者一般利用两种图式来指导学生分析题目：一种是逻辑图式，仍以“果园向外运输45吨苹果……还要运多少次”这道题目为例，在分析题目时，笔者首先为学生呈现了一张思维图式（如图1），从“还要运多少次”可以推导出“还有多少量要运”和“一次能运多少吨（1.5吨，已知）”；去除已知条件，我们需要求得的量是“还有多少需要运输”，那么显然就必须知道“总量有多少（45吨，已知）”“已经运了几吨”；去除已知条件，我们需要求得的量是“运了几次”，那么就需要知道“每次运几吨（2.5吨）”和“运了几次（9次）”，都是已知量，所以题目可解，解题为（45-2.5x9）÷1.5=15（次）.另一种是图象图式，仍以“果园运输”为例，分析题目时笔者给学生呈现了一张线段图（如图2），通过线段图，学生可以一目了然地看出，要求解“还需要运几次”，就必须知道“改用后需要运输多少量”，由线段图可知，就是用“总量”减去“已经运送的量”即可，从而题目也可解，借助逻辑图式可以帮助学生更好理解解题逻辑，理清解题思路；借助图象图式可以帮助学生更为直观地把握条件之间的关系，让学生更为准确、有效地找出解题线索.两种图式的有效运用，势必能有力提升学生的审题能力，增强审题效果.

利用逆向反证，验证审题思路

尽管已经有了较为有效的读题和分析题目的策略，但我们仍旧无法保证审题百分百正确，因此就需要我们通过逆向反证来验证我们的审题思路所谓逆向反证，是指学生将自身分析得出的审题思路，以三两句话的形式表述出来，再放回到题目中去验证，如果符合题意说明审题思路正确.因为逆向反证的过程中，学生需要从审题思路推导出解题思路，再与题目比对，这个过程要求学生准确理解题意，具有较为清晰的思维逻辑，因此不仅能够验证学生的审题思路，而且对于学生的审题能力、思维能力、表述能力的提升也颇有好处.

逆向反证笔者一般让两名学生为一组进行，这样有助于他们互相学习、互相检查.例如“一瓶洗衣液要18元，一瓶洗洁精要10元，请问两袋洗衣液和一瓶洗洁精一共多少钱？”这道题目，一名学生进行反证表述：“知道洗衣液和洗洁精的单价，知道买了两袋洗衣液和一瓶洗洁精，要求一共花了多少钱，分别求出洗衣液和洗洁精所花费的价格，再相加即可.利用到的公式是总价=单价×数量.”显然通过这名学生的逆向反证表述，我们可以发现该生对于题意的把握已经很到位，审题思路十分准确，又例如“某果园要向外运输45吨苹果，用一辆载重2.5吨的货车运了9次后，如果改用载重1.5吨的货车运，还要运多少次？”这道题目，有一名学生进行反证表述：“一个果园要向外运输45吨苹果，用2.5吨的货车运，需要运9次，如果改用1.5吨的货车运，需要运几次.2.5x9÷1.5=15次.”这名学生表述得很有自信，因为他的答案是正确的，但他的解题思路却完全错误了，如果没有通过逆向反证，学生就无法及时发现自己审题的错误，导致练习的错误.

小学数学应用题审题就好像人们出行前看地图，审题如果没做好就像出行路线没找好，最后肯定走不到预定的目的地，所以教师务必要十分重视学生应用题审题能力的培养.“有效读题识别关键信息”“借助图式分析审题策略”“利用逆向反证验证审题思路”这三条审题策略涵盖和体现了我们的审题逻辑，从这三方面人手培养学生的审题能力，方向是正确的，但在具体操作实践中，受限于小学生并不成熟的心智和逻辑思维能力，教师应该在趣味性、丰富性等方面多下工夫，让学生更易接受、更好理解，更为有效地提升审题水平，增强应用题答题能力.endprint