梁格法在四线大跨连续刚构桥上的应用
2016-03-09窦胜谭
窦胜谭
(铁道第三勘察设计院集团有限公司, 天津 300142)
梁格法在四线大跨连续刚构桥上的应用
窦胜谭
(铁道第三勘察设计院集团有限公司, 天津 300142)
以安家山河连续刚构桥为研究,文章采用专业有限元软件Midas建立了单梁与梁格模型,研究对比梁格模型与单梁模型的支座反力、内力、变形、应力、自振特性等内容,确认了所建的梁格模型准确无误。在此基础上对比梁格模型中各片纵梁的内力分配,得出了以下结论:(1) 合理的梁格划分可以高效的获得更加细致的结果,梁格法获得的正应力与单梁模型是吻合的,而剪应力、主应力结果差值较大,为获得特殊位置局部应力时应采用更加精细的有限元分析方法;(2) 梁格法可以获得多室箱型截面横向的弯矩分配,并依据弯矩分配,四线连续刚构铁路桥在运营时,一侧双线行车的情况下为最不利状态;(3)支座位置对连续刚构桥支座反力分布的影响明显,该连续刚构桥,支座最优位置为正对腹板中心线处。通过在梁格模型上改变支座间距,对比不同间距下支座反力,找出了支座布置的最优位置。
桥梁工程; 梁格法; Midas Civil; 支座位置优化; 连续刚构桥
1 梁格法简介
宽梁桥、斜交桥、曲线桥的单梁模型无法正确计算横向支座的反力、荷载的横向分布、斜交桥钝角处的反力以及内力集中效应,利用梁格法模型可以非常方便地解决以上问题。梁格法,通过划分成等效梁格,将纵向刚度分割成几部分纵梁刚度来承担,将横向刚度采用虚拟横梁等效模拟,比板壳、实体单元建模简单,计算量少,是一种高效的分析方法。
2 工程概况
本文选择位于兴县至保德地方铁路的一座相关桥梁作为研究对象。主桥采用(80+130+80)m四线连续刚构桥,引桥采用32 m简支梁。刚构桥桥面宽度22.8 m,梁端及跨中梁高4.8 m,中支点梁高9.2 m,梁底缘曲线段按2次抛物线变化。箱梁变高段底板按2次抛物线变化,下缘抛物线方程y=0.001 242 85x2,上缘抛物线方程y=0.001 059 247x2。本桥采用挂篮悬浇施工,最大悬浇段重5 098 kN,挂篮重采用2 500 kN,施工顺序采用先合龙中跨,再合龙边跨。
本桥采用Midas Civil 2010软件建立单梁模型进行整体计算,并在此基础上修改上部结构,建立空间梁格模型对单梁模型进行复核验算。
3 结构构造特点
3.1 上部结构
截面为单箱双室、直腹板、变高、变截面结构,箱梁顶宽22.8 m,底宽16.8 m。顶板厚0.45 m,腹板厚度从两端到墩处由0.5 m线性变化至1.3 m。底板厚按二次抛物线由0.45 m变至墩梁固结处1.05 m。桥梁上部结构横隔板设置在墩梁结合处、四分之一跨、四分之三跨及跨中位置,如图1、图2所示。

图1 上部结构示意图(cm)

图2 箱梁横截面示意图(cm)
3.2 支座初步位置
本桥采用单箱双室的三腹板截面,梁自由端采用三支座并排布置,以图3所示支座位置(d=7.4 m)为建模位置,在该位置处对比单梁与梁格模型的结果数据,可以复核单梁模型的结果,又可以获得各支座反力。调整梁格模型中支座位置,使三支座受力更加均匀,结构受力更加合理。
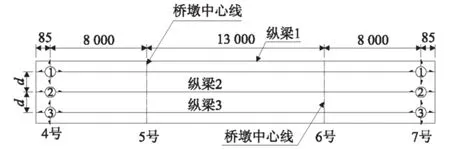
图3 支座位置(cm)
3.3 有限元模型
本文采用Midas Civil 2010建立有限元模型,单梁模型如图4所示:节点数187,单元数170;梁格模型如图5所示:节点数1 036,单元数1 682。采用基于腹板的方式划分截面,虚拟横梁采用工字型截面模拟,腹板厚度输入很小的值,在有横隔板的位置,虚拟横梁需按实际输入,纵向网格间距控制在1.5 m以内,具体形态如图6所示。

图4 有限元模型(单梁)

图5 有限元模型(梁格)

图6 梁格形态图
4 计算结果汇总分析
4.1 单梁模型与梁格模型对比
4.1.1 反力
以支座间距d=7.8 m(如图3)为研究对象,(4.1、4.2节)提取部分工况下单梁与梁格模型支座反力进行对比,如表1所示。
由表1可以看出,各位置反力基本一致,在各工况中,最小组合时反力差异较大,由于活载的影响差值占总反力的比重大。
4.1.2 内力
本文列出了各种荷载下关键位置的弯矩值,如表2、表3所示。
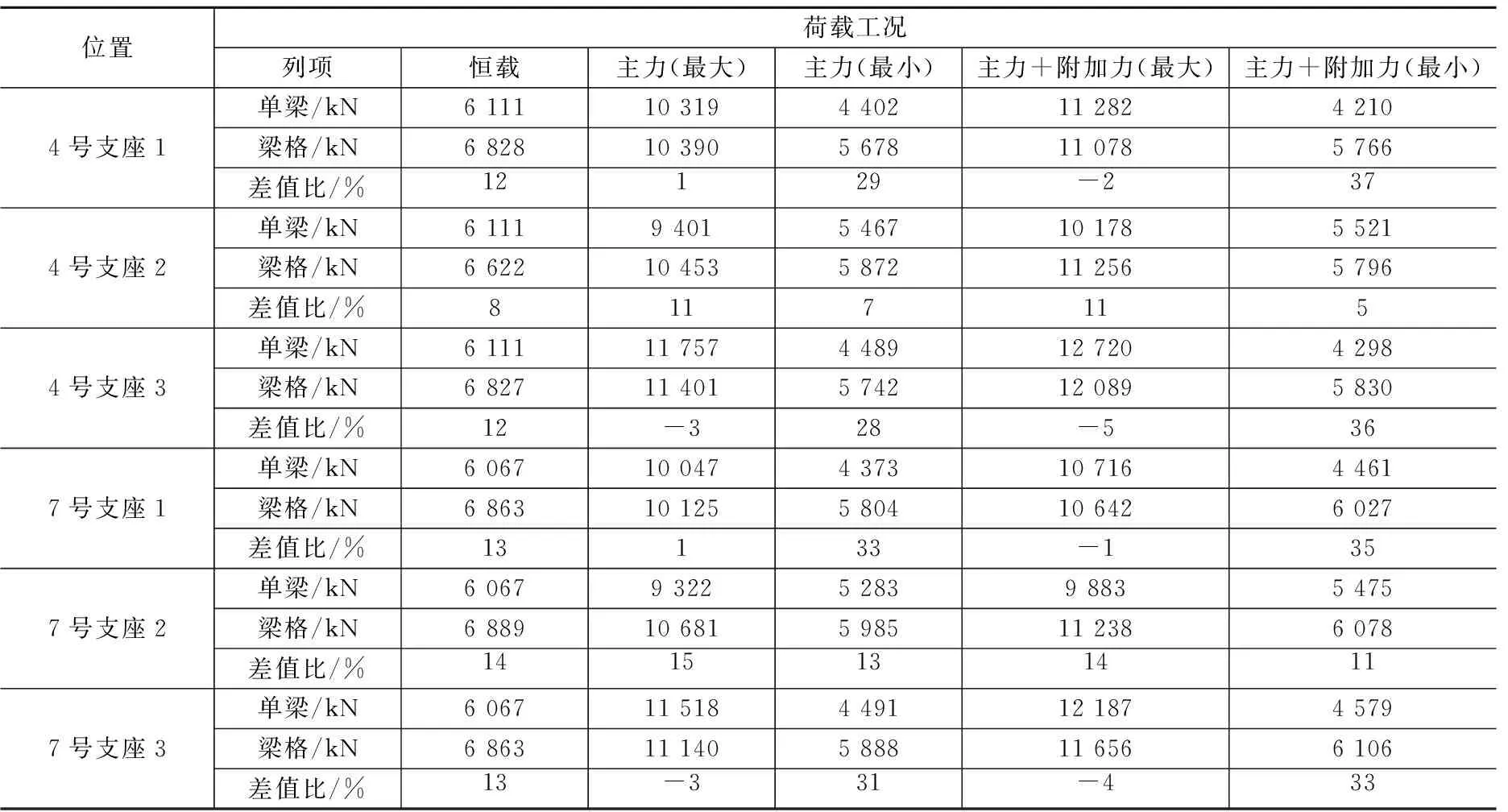
表1 单梁与梁格支座反力对比

表2 单梁与梁格弯矩对比(一)

表3 单梁与梁格弯矩对比(二)
由表2、表3可知,在恒载、活载(最大)、活载(最小)、钢束一次、钢束二次、整体升温、整体降温、收缩二次工况分别作用下,单梁与梁格模型的受力数值比较吻合。在徐变二次作用下,2个模型的数值差别较大,其原因是梁格模型将整体截面分割后,利用收缩徐变公式进行计算时,构件与大气接触的周边长度变大。
4.1.3 变形
通过对比变形,2种模型刚度略有差异,说明梁格模型在整体刚度上存在误差。对比活载作用下变形看出梁格模型的竖向挠度比单梁模型略小。对比主力或主力+附加力作用下变形看出梁格模型的竖向变形比单梁模型约大10℅,也就是说梁格模型比单梁模型在计算中偏于安全。
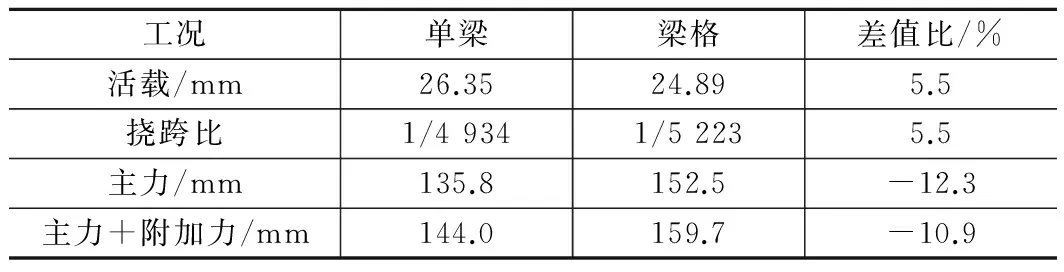
表4 主梁刚度对比
4.1.4 应力
从表5可以看出,正应力吻合较好,而剪应力、主应力差值较大,原因在于梁格法切割了截面以后破坏
了截面的整体性,改变了其中截面剪力流,而剪应力的差值也使得主应力差异较大。因此,梁格法的应力无法采信,在特殊位置局部应力分析时应采用更加精细的有限元分析方法。

表5 应力对比 (MPa)
4.1.5 自振特性
为了解梁格法对自振特性的影响,提取前五阶自振频率及振型对比。
由表6自振频率及振型可以看出,单梁模型与梁格模型在第三阶产生差异,说明梁格法切割梁截面后对其模型的扭转刚度是有影响的,其扭转刚度要小于单梁模型。

表6 单梁模型自振特性 (Hz)
4.1.6 小结
通过以上四小节对比,可以看出该梁格模型能够准确地分析该连续刚构桥的受力情况,进而可以进行以下两小节的对比分析。
4.2 梁格自身对比
选关键位置,提取梁格模型中四线活载(最大)、一侧双线活载(最大)、一侧单线活载(最大)作用下各纵梁单元弯矩,表7列出了各纵梁关键位置处的弯矩,梁格模型共有3根纵梁,按由下至上的顺序,定义3根纵梁分别为纵梁1、纵2梁、纵梁3。

表7 相同位置处各纵梁弯矩数值 (kN·m)
从表7可以看出,各纵梁中,承担的弯矩不同,四线活载下,中间纵梁承担较大弯矩;一侧双线行车下,列车所在侧的纵梁承担弯矩最大,中间次之,另一侧较小;一侧单列荷载下,也是列车所在侧弯矩最大,中间次之,另一侧最小。对比3种工况,可以看出,梁格法可以获得各片纵梁承担的弯矩,而且四线连续刚构铁路桥在一侧双线行车的情况下为最不利状态。
4.3 梁格模型支座位置优化
保持该梁格模型各条件不变,仅改变两端支座间的间距,d(如图3)分别取值为6.8 m、7.4 m、7.8 m,提取有代表性的几种荷载工况下支座反力,如表8所示。

表8 支座反力汇总 (kN)
为方便看出其变化趋势,选取主力(最大)、主力+附加力(最大)下各支座反力列于图7~图10。

图7 主力(最大)组合下4号墩各支座反力

图8 主力(最大)组合下7号墩各支座反力

图9 主力+附加力(最大)组合下4号墩各支座反力

图10 主力+附加力(最大)组合下7号墩各支座反力
从支座反力可以看出,在不同间距的情况下,支座反力具有类似的分布趋势,为获得反力控制值,将2种间距下所有支座反力最大值列于表9。

表9 支座反力控制值
由数据变化趋势分析可知:支座间距不同时,在各荷载工况下,支座反力分布均为边支座大、中支座小;横向的3个支座,边支座与中支座的间距越大,中间支座的支反力越大;在各荷载工况(最大)组合下,间距越大,横向3个支座承担反力的数值越接近。因此,确定支座间距在7.8 m处(腹板位置)为最优位置。安家山河铁路桥所选用的支座承载力为15 000 kN,因此,3种间距下承载力均可满足要求。由于该桥底板宽度为16.8 m、支座垫板横向宽1.3 m,为保证支座处局部应力满足规范要求,并防止结构边缘应力集中产生损伤,安家山河铁路桥支座间距采用7.4 m。
5 结论
(1)合理的梁格划分可以高效地获得更加细致的结果,为设计做出指导。本文所建立的梁格模型能够准确模拟该连续刚构桥的受力情况。
(2)梁格法获得的正应力与单梁模型是吻合的,而剪应力、主应力结果差值较大。因此,梁格法获得的应力无法采信,在特殊位置局部应力分析时,应采用更加精细的有限元分析方法。
(3)梁格法可以获得宽截面连续刚构桥中各片纵梁承担的弯矩。四线连续刚构铁路桥在运营时,一侧双线行车的情况下为最不利状态。
(4)通过支座在不同位置下支座反力的对比,可以看出支座位置对连续刚构桥支座反力分布的影响明显,该连续刚构桥,支座最优位置为腹板位置处(支座横向间距7.8 m)。本文中安家山河铁路桥支座承载力为15 000 kN,因此,3种间距布置均可满足要求。受桥梁底板宽度及支座垫板宽度限制,为保证支座处局部应力满足规范要求,并防止结构边缘应力集中产生损伤,实桥支座间距采用7.4 m。
[1] 延力强,杨欣然.梁格法在松花江特大桥设计上的应用[J].铁道工程学报,2010,26(12):37-41. YAN Liqiang,YANG Xinran.Application of Grillage Method in Designing Songhua River Grand Bridge[J].Journal of Railway Engineering Society, 2010,26(12):37 -41.
[2] E.C.汉勃利[英]主编.桥梁上部构造性能[M].郭文辉,译.北京:人民交通出版社,1982. E.C.Hambly[Britain] Chief editor. Bridge Deck Behaviour[M]. Translated by GUO Wenhui.Beijing: China Communications Press,1982.
[3] TB 10002.3-2005 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB 10002.3-2005 Code for Design on Reinforced and Prestressed Concrete Structure of Railway Bridge and Culvert[S].
[4] 王富万,杨文兵.梁格法在桥梁上部结构分析中的应用[J].华中科技大学学报(城市科学版),2006,23(S1):80-82. WANG Fuwan, YANG Wenbing. Application of Grillage Method in Bridge Decks Analysis [J]. J. of HUST.(Urban Science Edition), 2006,23(S1): 80-82.
[5] 杨林.空间梁格法对扁平型钢箱梁结构分析[D].西安:长安大学,2010. YANG Lin.Analysis on The Flat Steel Box Girder by Space Grillage Method[D]. Xi’an: Chang’an University,2010.
[6] 张元凯.弯箱梁梁格实用计算分析[D].上海:同济大学土木工程学院,2000. ZHANG Yuankai. Grillage Practical Computational Analysis of Curved Box Girder[D]. Shanghai: Civil Engineering Institute of Tongji University ,2000.
[7] 刘瑶.梁格法在分析箱梁结构中的应用[D].哈尔滨:东北林业大学土木工程学院,2007. LIUYao. The Application of Grillage Method in Analyzing Box Girder Structure[D]. Harbin: Civil Engineering Institute of Northeast Forestry University, 2007.
[8] 李捷.梁格法在桥梁上部结构分析中的应用[J].中国新技术新产品,2008,25(11):68. LI Jie.Grillage Method Used in The Analysis of The Bridge Superstructure[J]. China New Technologies and Products, 2008,25(11):68.
Application of Grillage Method in Four-line Long-span Continuous Rigid Frame Bridge
DOU Shengtan
(The Third Railway Survey and Design Institute Group Corporation, Tianjin 300142, China)
Taking Anjiashan river continuous rigid frame bridge as background, in this paper, the bearing reaction , internal force, deformation, stress, natural vibration characteristics etc. of grillage model and single beam model are studied and compared by using the professional finite element software Midas, and the grillage model founded in this paper is confirmed accurate. On this basis, a conclusion is obtained from the internal force distribution of each longitudinal beam: (1) Reasonable beam meshing can obtain more detailed results efficiently,and normal stress got from grillage method is consistent with the stress from single beam model, while shear stress and primary stress are not. More sophisticated finite element analysis should be used to obtain local stress for the special position. (2) Grillage analysis method can get bending moment distribution of box cross-section, and find out the moment distribution of box beam under the worst status-double line driving on the same side during the operation of four-line continuous rigid frame railway bridge. (3) The support position has great effects on support reaction distribution, and where directly facing the web centerline is the best support position for in this kind of bridge. Finally, the optimal support position is found out by changing distance between supports on beam grillage model and comparing the reaction under different distance.
bridge engineering; grillage method; Midas Civil; support position optimized; continuous rigid frame bridge
2015-11-09
窦胜谭(1988-),男,助理工程师。
1674—8247(2016)01—0036—06
U448.23
A
