基于三角模糊数-TOPSIS的绿色施工评标方法

罗党, 孙慧芳， 毛文鑫

(华北水利水电大学,河南 郑州 450045)

基于三角模糊数-TOPSIS的绿色施工评标方法

罗党, 孙慧芳， 毛文鑫

(华北水利水电大学,河南 郑州 450045)

科学合理的评标方法对于优选具备绿色施工能力的承包人至关重要。现有的评标方法中存在定性指标较多、专家评标时评标语言模糊等问题。结合绿色施工的标准和要求,构建绿色施工招标评标体系,并建立了基于三角模糊数-TOPSIS法的绿色施工招标评标模型，最后通过实例验证了该评标模型的科学性和实用性。

绿色施工;评标方法;三角模糊数;TOPSIS

工程项目评标属于多目标、多准则的决策问题,目前解决该类问题研究较多的有层次分析法(Analytic Hierarchy Process,AHP)、模糊综合评价法和主成分分析法等。王伟等将AHP用于机场勘察项目评标体系中,并建立了决策模型[1]；但该方法在指标较多时会导致判断矩阵不一致的情况发生,并且调整繁琐、计算量大。孙现军将主成分分析法应用到清单商务标评标领域,建立了工程评标综合评价模型,通过计算得出评标结果与实际相符合[2]；但主成分分析法会导致部分信息丢失,对结果有所影响。李丹等通过对影响高校物资招标采购的因素进行分析,将模糊综合评价理论用于评标工作中,具有一定的应用价值[3]；但该方法存在指标因素越多其权重会越小的缺陷,而对评判结果产生影响。

针对上述方法存在的缺陷,考虑到绿色施工评标体系的复杂性：既有定性指标又有定量指标,且只有少数指标能进行定量分析,对于大部分指标，决策者无法给出精确的数据,如企业信誉、履约情况、资质概况、施工经验等用好、一般、差等来表示更符合绿色施工评标的评价原则。于是,本文将三角模糊数原理和理想解法(TOPSIS)有机地结合起来,建立了基于三角模糊数的TOPSIS综合评标模型。该模型避免了AHP中指标过多从而导致权重难以确定的缺点；同时，相比主成分分析法，该模型信息丢失得更少,结果更加客观合理,而且比模糊综合评判法计算出来的结果分辨率更高。因此，利用该模型进行绿色施工招标评标项目的优选,会使评价结果更加科学合理,更加切合实际。

1 绿色施工项目评标指标体系的构建

绿色施工项目评标指标体系的构建是否科学合理,对于评标结果的准确性有很大的影响。因此,构建绿色施工评标体系,除了要满足投标报价、施工技术方案等基本要求,还要涵盖绿色施工的有关技术要求。鉴于此,本文根据传统建筑施工的评标体系,参照国内外各种绿色建筑的评价指标[4-5],结合绿色施工的特点和核心理念[6-7]——节能减排,具体表现为“节能、节地、节水、节材和环境保护”,即“四节一环保”,建立绿色施工招标评标指标体系，见表1。该体系以投标企业的资质与信誉、绿色施工技术方案和商务报价3个方面为一级指标,同时涵盖10个二级指标。

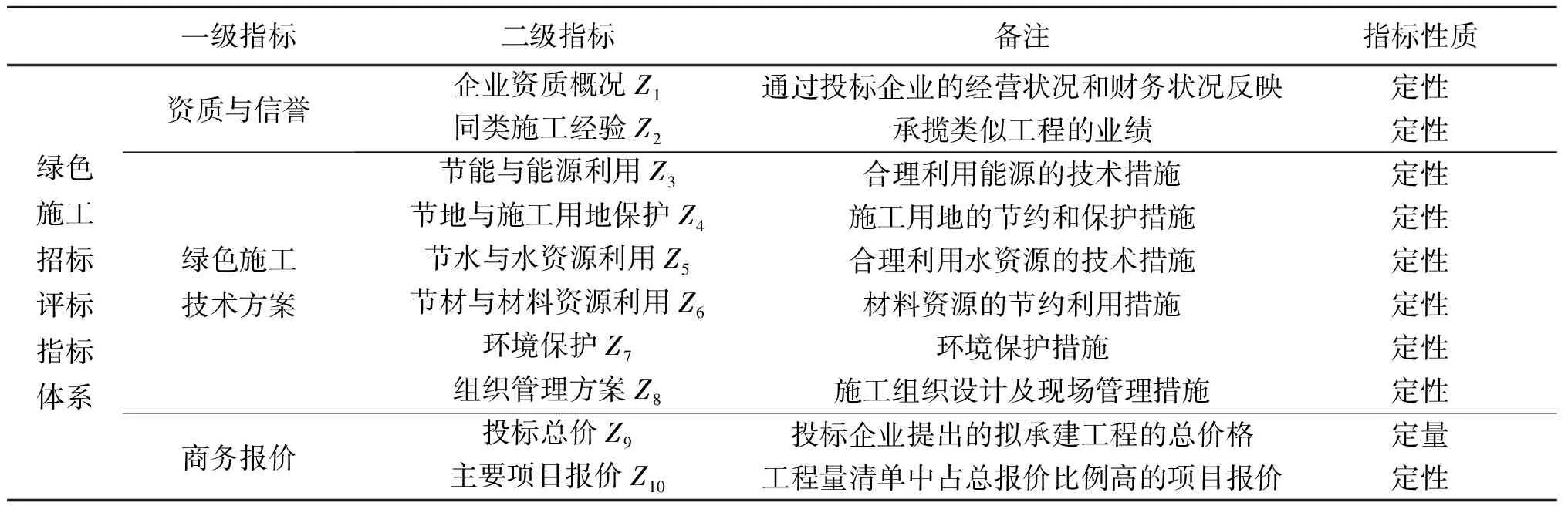
表1 绿色施工招标评标指标体系

2 基本理论

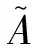
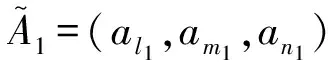
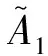
(al1+al2,am1+am2,an1+an2),

(μal1,μam1,μan1)(λ≥0,λ∈R),

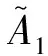
(al1al2,am1am2,an1an2)。

式中⊕和⊗分别为模糊运算的加法和乘法运算符号。

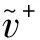
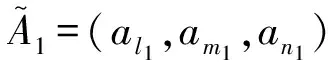
E0=

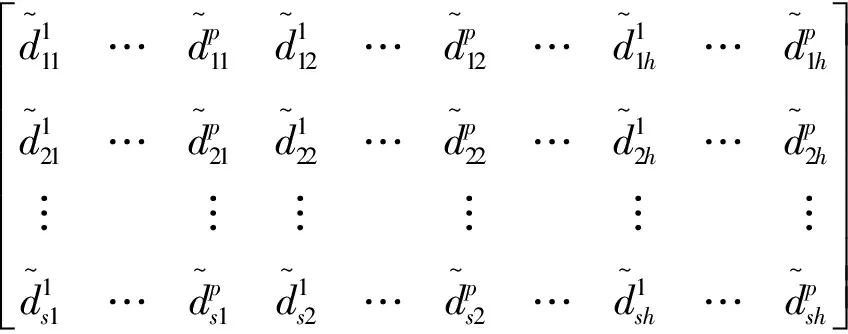
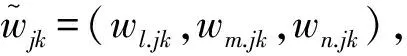
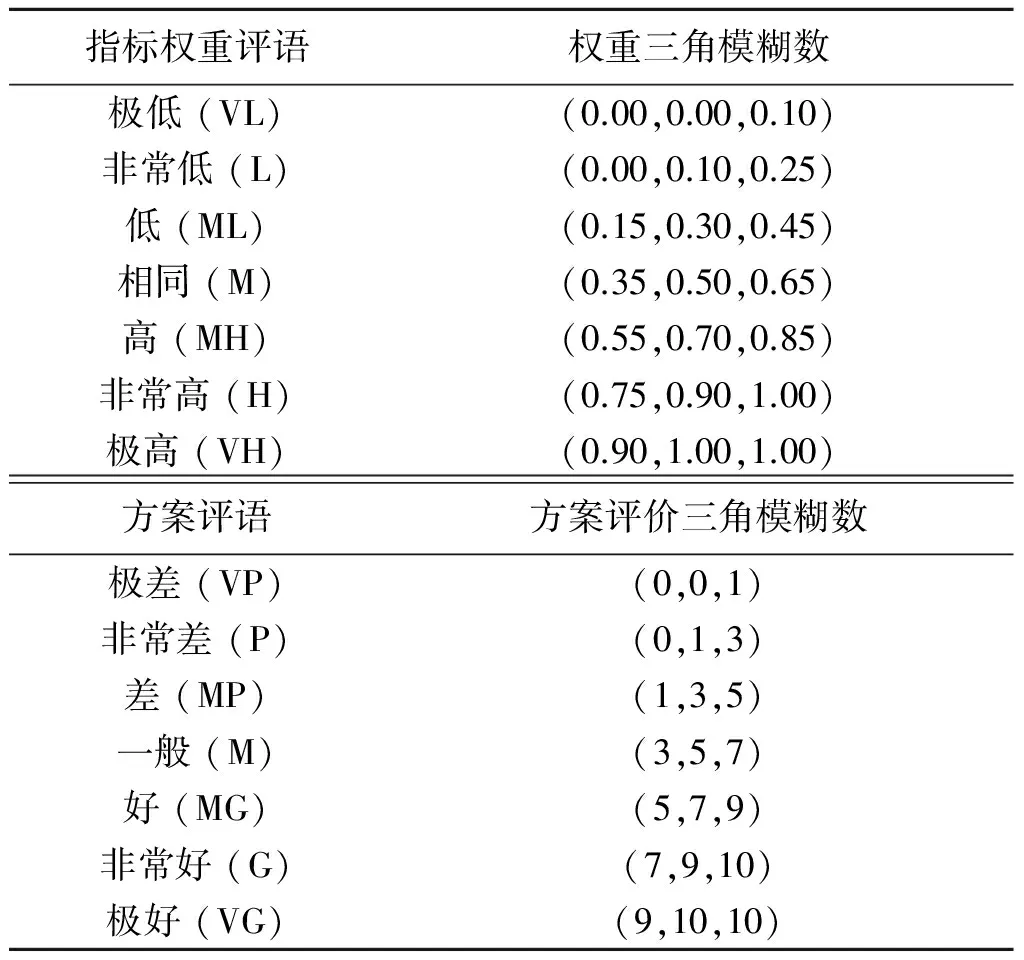
表2 指标权重与方案语言项的三角模糊数对照表

3 评标方法

基于三角模糊数的TOPSIS绿色施工评标步骤如下:

步骤1 构建绿色施工评标指标体系。

步骤2 构建模糊集结方案矩阵E和权重向量W。根据表2，由定义5和6得模糊群决策方案矩阵E0和权重矩阵W0,综合各方面专家的意见,挑选p位涵盖业主、施工单位代表、政府主管部门代表、绿色施工领域技术评价专家等具有代表性的专家,对E0进行方案评价信息的集结,得模糊集结方案矩阵E,即

E=[(al.ij,am.ij,an.ij)]s×h=

(1)

由W0对各属性的重要性评价进行集结，得模糊集结属性权重向量W,即

W=[(wl,j,wm,j,wn,j)]1×h=

(2)

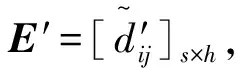
(3)

(4)

步骤6 计算各投标方案的排队指示值Ci,根据Ci从大到小的顺序给出对应方案的优劣次序。Ci最大值对应的方案为最优方案。

(5)

4 实例分析

拟采用绿色施工技术的某工程项目,现有3家投标企业通过资格预审可供选择,即Y=(Y1,Y2,Y3)为方案集,各投标企业的报价分别为6亿元、10亿元和8亿元,Z=(Z1,Z2,Z3,Z4,Z5,Z6,Z7,Z8,Z9,Z10)为属性集,聘请4位专家(业主、施工单位代表、政府主管部门代表、绿色施工领域技术评价专家各1名)，即专家集为X=(X1,X2,X3,X4),参照表2的语言项对各投标方案在各属性下的好坏和各属性的重要性进行评价(评价结果见表3和表4)。

步骤1 建立绿色施工招标评标指标体系(见表1)。

步骤2 由表3的语言评价值,根据表2转化为对应的三角模糊数,对方案评价信息进行集结,由式(1)得模糊集结方案矩阵E。

E=[(al.ij,am.ij,an.ij)]3×10=

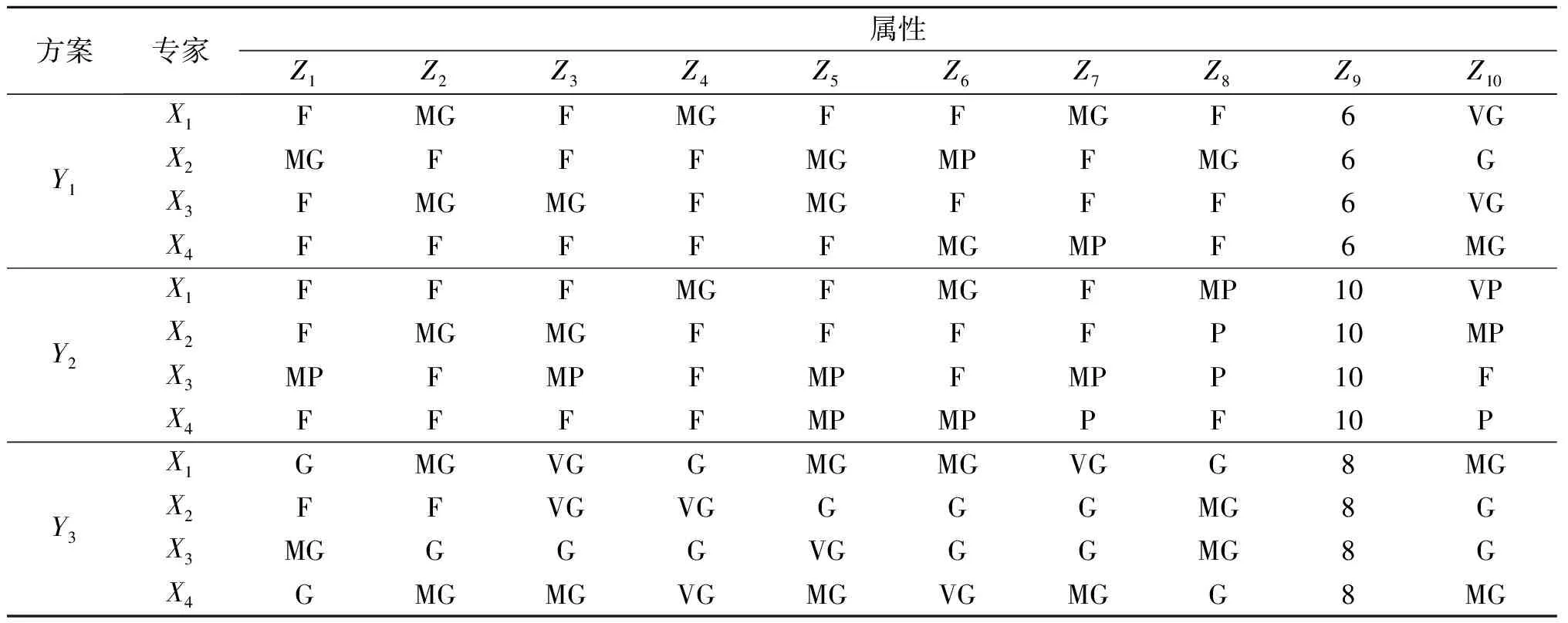
表3 各专家对各投标方案在各属性下的语言评价

表4 各专家Xk对各个属性Zj重要性的语言评价

综合4位专家的意见,利用式(2)得模糊集结属性权重向量W。

W= [(wl.j,wm.j,wn.j)]1×10=

[(0.16,0.30,0.45),(0.25,0.40,0.55),

(0.55,0.70,0.84),(0.65,0.80,0.93),

(0.60,0.75,0.89),(0.83,0.95,1.00),

(0.69,0.83,0.93),(0.35,0.50,0.65),

(0.69,0.83,0.93),(0.60,0.75,0.89)]。

步骤3 对E利用式(3)进行规范化处理得标准决策矩阵E′,

步骤4 考虑每个属性指标的权重,由式(4)得模糊加权决策矩阵G,

G=[(tl,ij,tm,ij,tn,ij)]3×10=

步骤5 由定义3和4计算各投标方案到模糊正理想解和模糊负理想解的距离分别为：

步骤6 计算各投标方案的排队指示值Ci：

C1=0.456,C2=0.327,C3=0.579。

由此对方案进行排序：

Y3Y1Y2。

为了进一步说明本文方法的合理性，下面采用文献[3]中的模糊综合评价方法对上述问题进行求解。取V={V1,V2,…,V6}={100，85，70，55，40，25}为评价集，得到各投标方案的模糊综合评价结果分别为：BY1=(0.457，0.412，0.131，0，0，0),BY2=(0.351，0.324，0.325，0，0，0),BY3=(0.385，0.372，0.243，0，0，0)。将模糊综合评价结果与评价集V进行模糊运算，得到各投标方案的得分分别为:PY1=89.89,PY2=85.39,PY3=87.13。于是各方案的优劣顺序为：Y1Y3Y2。与本文的评标结果相比，方案Y1和Y3的顺序发生了变化。而在实际工程中，由于绿色施工技术水平对于评标结果的影响较大，而方案Y1相比Y3的绿色施工技术水平较低，在其他评标因素对结果影响相差不大的情况下,方案Y3应优于Y1，即本文的评标方法更合理。

5 结 语

绿色施工是一个技术性较强及较新的领域,其评标的标准和方法还需要不断探索和检验修正。本文针对评价指标多数为定性指标,评价语言具有模糊性的特点,利用三角模糊数将定性问题定量化,使评价过程更加客观、公正、合理,最后通过算例分析验证了该方法的有效性和实用性。

[1]王伟,王健.层次分析法在机场勘察项目评标决策中的应用[J].项目管理技术,2015,13(9):72-77.

[2]孙现军.基于主成分分析法的清单商务标评标方法及应用[J].建筑经济,2011(7):58-61.

[3]李丹,董志国.模糊综合评价模型在评标中的应用——以高校物资采购为例[J].河南科学,2012,30(11):1669-1671.

[4]李海涛,张晓兵.基于改进FAHP赋权的绿色施工招标评标模型[J].数学的实践与认识,2013,43(17):27-34.

[5]李美云,范参良.绿色施工评价指标体系研究[J].工程建设,2008,40(1):56-60.

[6]王有为.绿色施工:绿色建筑核心理念—《绿色施工导则》技术要点解读[J].建设科技,2008(3):89-91.

[7]申琪玉,李惠强.绿色建筑与绿色施工[J].科学技术与工程,2005(21):1634-1638.

[8]王明和.基于语言变量的房地产项目投资风险评价研究[D].北京:北京交通大学,2012.

[9]徐泽水.三角模糊数互补判断矩阵排序方法研究[J].系统工程学报,2004,19(1):85-88.

[10]Wang J W,Cheng C H,Huang K C.Fuzzy hierarchical TOPSIS for supplier selection[J].Applied Soft Computing,2009,9(1):377-386.

(责任编辑：陈海涛)

Bidding Evaluation Method of Green Construction Based on Triangular Fuzzy Number and TOPSIS

LUO Dang, SUN Huifang, MAO Wenxin

(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

Scientific and reasonable tender evaluation method is crucial for optimizing the contractor of green construction ability. The problems which more qualitative indicators exist in the existing evaluation methods and the evaluating language is fuzzy when experts the bid evaluate. This paper combined the green construction standards with requirements, tendering and bidding evaluation system of Green Construction is constructed, and established tendering and bidding model of green construction based on triangular fuzzy numbers TOPSIS. Finally, the example results prove that this model is scientific and practical.

green construction; bidding evaluation method; triangular fuzzy numbers; TOPSIS

2015-12-04

国家自然科学基金项目(71271086)；河南省科技厅重点科技攻关项目(142102310123)；河南省高等学校重点科研资助项目(15A630005)。

罗党(1959—),男,河南汝南人,教授,博导,博士,主要从事灰色系统理论与决策分析研究。E-mail:iamld99@163.com。 孙慧芳(1990—),女,河南平顶山人,硕士研究生,主要从事建设项目管理研究。E-mail:1791972041@qq.com。

10.3969/j.issn.1002-5634.2016.02.013

TV512;TU72

A

1002-5634(2016)02-0073-05