盾构隧道施工注浆参数合理取值的简化算法
2016-03-09黎春林孙玉永陈静
黎春林, 孙玉永, 陈静
(铜陵学院 建筑工程学院,安徽 铜陵 244000)
盾构隧道施工注浆参数合理取值的简化算法
黎春林, 孙玉永, 陈静
(铜陵学院 建筑工程学院,安徽 铜陵 244000)
在盾构隧道施工中,临近隧道部分土体因应力扰动产生变形,土体变形大小与注浆参数密切相关。为分析盾构施工对临近土层强度破坏和变形的影响,根据土体的强度破坏准则,研究了注浆压力的合理取值范围,并从施工安全的角度提出了最优注浆压力的确定方法;然后,采用镜像法分析了注浆量和地表沉降的关系,并通过和工程现场实测数据的对比分析,得出地表位移和注浆量基本呈线性关系这一结论。在此基础上,提出了以控制沉降为目标来确定最佳注浆量的一种简化计算方法。
盾构隧道;注浆压力;注浆量;地表沉降
发展轨道交通已成为城市解决交通拥堵问题的首选途径[1],但盾构施工使得周围地层应力状态发生了变化,并引起土体出现过大变形。统计资料显示,已建和在建的隧道中,超过35%的隧道会产生沉降[2]。要减小隧道周边土体的变形,应对盾尾空隙进行及时注浆回填,壁后注浆控制技术是盾构施工的关键[3]。注浆不但可以降低地层损失,而且可在隧道周围土层中形成一个加固支撑圈,提高土体本身的承载能力。
在进行注浆操作时,注浆压力和注浆量是非常重要的施工参数。注浆压力和注浆量过小,不能满足填充盾尾空隙的要求;注浆压力和注浆量过大又会造成土体的被动挤压破坏和浆液的浪费。所以,在盾构施工过程中,注浆压力和注浆量是否合理对管片支护力的设计和土体内塑性区范围的扩展都会产生很大的影响。
对盾构隧道注浆参数的控制是当前的一个研究热点。刘健等[4]通过试验对盾构壁后注浆浆液的扩散规律及因注浆而造成的管片压力进行了研究,研究成果可用于指导盾尾注浆工艺参数的选择;朱才辉等[5]将间隙参数归纳为注浆填充率、支护压力比和偏心超挖率3个参数,并采用有限元方法对其进行地表沉降规律的量化分析;Verruijt等[6-11]应用镜像法建立了地层损失和地面沉降关系的解析公式;黎春林[12]通过有限元软件研究了不同注浆压力下隧道周边土体超孔隙水压的分布和消散规律;苟长飞等[13]采用流体力学理论对盾尾同步注浆浆液充填压力环向分布模型及相关参数进行了分析;叶飞等[14]将同步注浆对地层的影响简化为半无限弹性体中的柱形孔扩张问题,推导了同步注浆对地表变形影响的公式;邱明明等[15]采用力学方法研究了盾构同步注浆压力分布统一的计算模型。
近年来,虽然盾构注浆取得了很多研究成果,但在实际工程中,尚缺乏简便实用的定量化分析盾构施工土体强度及变形与施工参数关系的理论公式。笔者根据土体强度理论,通过分析注浆的作用机理及注浆参数与土体变形的关系,提出易于施工人员理解和工程应用推广的盾构施工注浆参数计算公式。
1 注浆压力安全范围
盾构推进会在盾尾留下空隙,盾尾注浆后,浆液在空隙中开始呈流动状态,注浆压力直接作用在土体上阻止土体下沉;随后浆液固化,浆液主要起充填作用,将其承受的土压力传递给管片,固化后的注浆体和管片一起支撑土体,阻碍其进一步变形。注浆压力不能太小,否则土体失去支撑产生过大沉降;但注浆压力也不能太大,否则会造成周边土体的劈裂。注浆压力一般根据隧道埋深计算的水土压力及盾构施工的具体条件来确定。本文根据土体极限平衡理论来预估注浆压力的合理范围并确定最优注浆压力值,分别从土体不出现塑性区和不出现破坏两个方面进行探讨。
1.1 最小注浆压力
1.1.1 使土体不出现破坏的最小注浆压力
最小注浆压力必须维持土块的稳定,使之不下塌、不出现主动破坏,即:
(1)
式中:σa为注浆压力,kPa;H为隧道轴线埋深,m;γ为土层的容重,kN/m3;c为土体的黏聚力,kPa;φ为土体的内摩擦角,(°)。
很显然,由式(1)得到的最小注浆压力在实际工程中是不能采用的,因为土体已经处于极限平衡状态,濒临破坏,施工时实际注浆压力应该在其基础上再乘以安全系数以保证安全。
1.1.2 使土体不出现屈服的最小注浆压力
许多学者以弹塑性理论为基础,研究了圆形隧洞围岩应力和稳定情况,分析了塑性区范围和隧道支护压力的关系,其中应用最广的是芬纳公式和卡斯特奈公式。根据芬纳公式[16],塑性区范围R′为:
(2)
式中:a为隧道半径,m;σ0为地层原始应力,kPa。
若使隧道周围不存在塑性区,即R′≤a,由式(2)可求得注浆压力:
σa≥(1-sinφ)σ0-ccosφ。
(3)
由式(3)得到的最小注浆压力在实际工程中采用是偏于安全的,一般情况下土体内是允许出现塑性区的,只要控制塑性区的发展不超过一定的区域就能保证施工安全。
1.2 最大注浆压力
1.2.1 使土体不出现破坏的最大注浆压力
最大注浆压力必须限制在某一范围,使土体不出现隆起、不发生被动破坏,即:
(4)
同理,式(4)计算得到的最大注浆压力必须除以安全系数才能在施工中采用。
1.2.2 使土体不出现屈服的最大注浆压力
由小孔扩张理论[16],此时盾构隧道施工的扰动半径R为:
(5)
在土体受压的情况下,若要使隧道周围不出现塑性区,即R≤a,由式(5)可求得最大注浆压力为:
σa≤(1+sinφ)σ0+ccosφ。
(6)
1.3 注浆压力的合理范围
1.3.1 土体不出现塑性区时的注浆压力范围
综合考虑土体受挤压和松弛两种状态,如果要求土体完全在弹性状态下工作,这时注浆压力的选取范围是
(7)
1.3.2 土体不出现破坏时的注浆压力范围
如果要求盾构在施工中土体不出现主动或被动破坏,则理想的注浆压力的选取范围是:
(8)
1.4 最优注浆压力
为了方便对问题的讨论,在这里引入安全系数F。由式(1)可知,当注浆压力较小、土体松弛时,其安全系数为:
(9)
由式(4)可知,当注浆压力较大、土体受挤压时,其安全系数为:
(10)
从安全角度考虑,为了保证土体既不出现主动破坏,又不出现被动破坏,则最优的注浆压力应该使式(9)和(10)的安全系数相同,故有:
(11)
则安全系数F可表示为:
(12)
由式(12)可知,土质条件越好,则F值越大,施工越安全。式(12)可用于盾构施工安全方面的土质条件的评估。
实际注浆压力还需要考虑其沿程阻力损失Δσ,Δσ大小一般取20~30 kPa。所以实际的注浆压力为:
σ实际=σ最优+Δσ。
(13)
1.5 实例分析
某盾构区间,隧道轴线埋深15 m。根据勘察资料,试验路段土体各层的厚度及地质参数见表1。
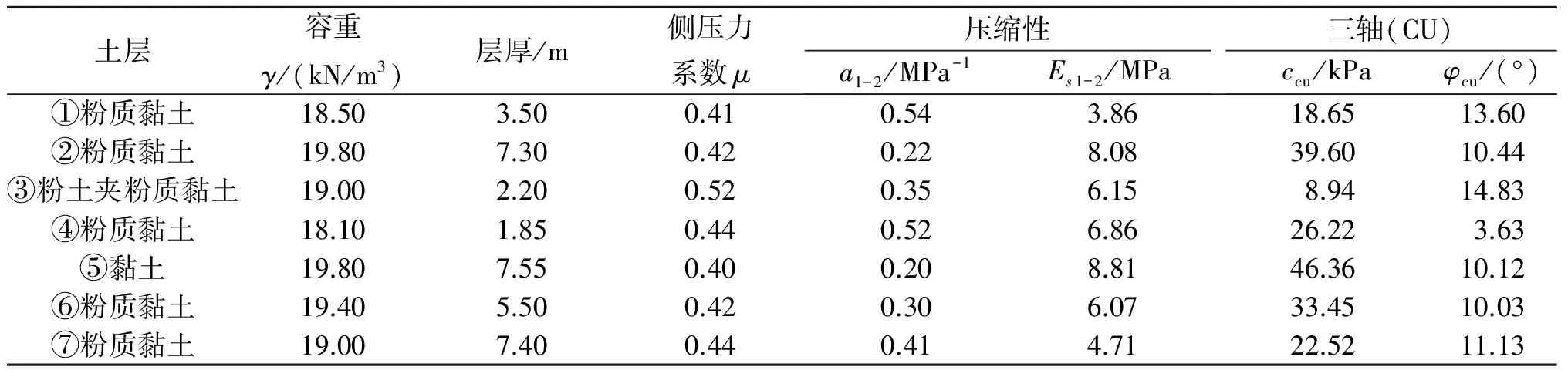
表1 试验区间地层的物理、地质参数
注:a1-2和Es1-2分别为土压力在100~200 kPa时的压缩系数和压缩模量;φcu和ccu分别为固结不排水剪试验测得的土的内摩擦角和黏聚力。
γ、c和φ分别按隧道穿越土层及上覆土层(①—⑤层)的厚度取其加权平均值,根据表1计算得:γ=19.4 kN/m3,c=34.5 kPa,φ=10.7°。
如果要求土体不出现主动或被动破坏,由式(7)可得:
σa下≥(1-sinφ)σ0-ccosφ=
(1-sin10.7°)×288-34.5×cos10.7°=
200.6 (kPa),
σa上≤(1+sinφ)σ0+ccosφ=
(1+sin10.7°)×288+34.5×cos10.7°=
375.4 (kPa)。所以σa的取值区间为[200.6 kPa,375.4 kPa]。则施工安全系数F为
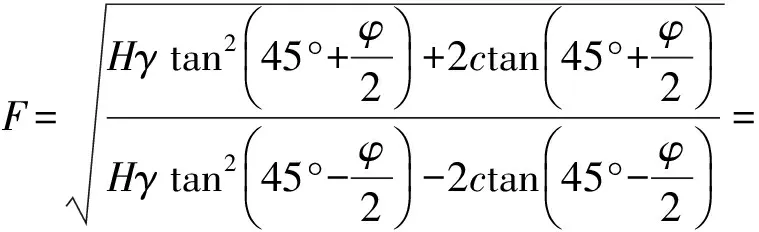
1.89;
1.89=142.1×1.89=269 (kPa)。
因此,从安全角度考虑,该盾构区间段最优的注浆压力(不考虑沿程阻力损失)取269 kPa。
2 注浆量的取值
研究表明,地层损失是引起地表沉降的主要因素,而控制地层损失,必须正确估计注浆量。特别是在软土地层施工,因为土体强度较低,一般不能自承,当盾尾脱出管片时,如果注浆量不足,因存在建筑空隙,土体失去支撑后将迅速向管片方向塌落,引起隧道附近地层变形和土体强度下降。下文应用镜像法分析地层损失引起地层移动的机理,并建立注浆量与地表沉降之间的简易函数关系。
2.1 理论注浆量
在盾构隧道施工中,地层损失往往呈非均匀分布,Loganathan等[17]建议采用非等量径向土体变形模式,如图1所示。

图1 地层损失非均匀分布示意图
在地层损失非均匀分布模式下,Loganathan等在Sagaseta[18]解析解的基础上,并考虑土体的压缩性,应用镜像法推导出地面沉降的计算公式:
(14)
式中:Sz=0为地面沉降量,m;R为隧道半径,m;μ为土的泊松比;Vs为地层损失量,m3/m。
在地层损失非均匀分布模式下,Vs的计算公式为:
πR0ga≈πRga。
(15)
式中R0为开挖截面的半径,m。
将式(15)代入式(14)得
(16)
理论注浆量V′可由下式计算:
(17)
式中:V′为理论注浆量,m3/m;D0为盾构掘削外径,m;D为隧道外径,m;ga为地层损失参数,m。
地层损失参数ga和地层损失率η之间的关系可由式(15)推导如下:
Vs=πR2η≈πRga,
则
ga≈Rη。
(18)
式中:η为地层损失率,其大小一般为0.2%~2.0%,具体取值可参照文献[19]的研究成果。
式(16)—(18)建立了地表沉降和理论注浆量的函数关系。由注浆量可以计算对应的地表沉降;如果已知沉降控制标准,也可以反过来求取施工应采用的注浆量。
2.2 实际注浆量
因浆液在运输和注浆过程中会有损耗、盾构超挖和纠偏、浆液劈裂渗透一部分到周边地层、充填材料本身体积在固化过程中及注浆压力作用下压密等因素影响,实际注浆量要比式(17)计算的注浆量大得多,两者关系为:
(19)
式中:α为与土质相关的注浆参数,根据现场实测数据,在软土地区,该值一般为1.5~2.6。其中黏性土多在1.5~1.7范围内,砂性土多在1.7~2.2范围内。
2.3 最佳注浆量
式(19)计算得到的注浆量包含太多的理论和经验因素,不一定符合工程实际。所以应在施工现场进行地表沉降实测,在对实测值和理论值进行比较分析的基础上,由地表沉降和注浆量的相关关系可推导出该地质条件下的最佳注浆量。
下面以某盾构区间为例,说明最佳注浆量的确定方法。
该试验段地表无重要建筑物,地质条件见表1。在施工现场沿隧道纵向轴线每5.00 m埋设1个测点桩,沿隧道横向对称于隧道轴线向两边每隔3.25 m打1个测点桩。测量使用高精度的水准仪和经纬仪,测点布置如图2所示。
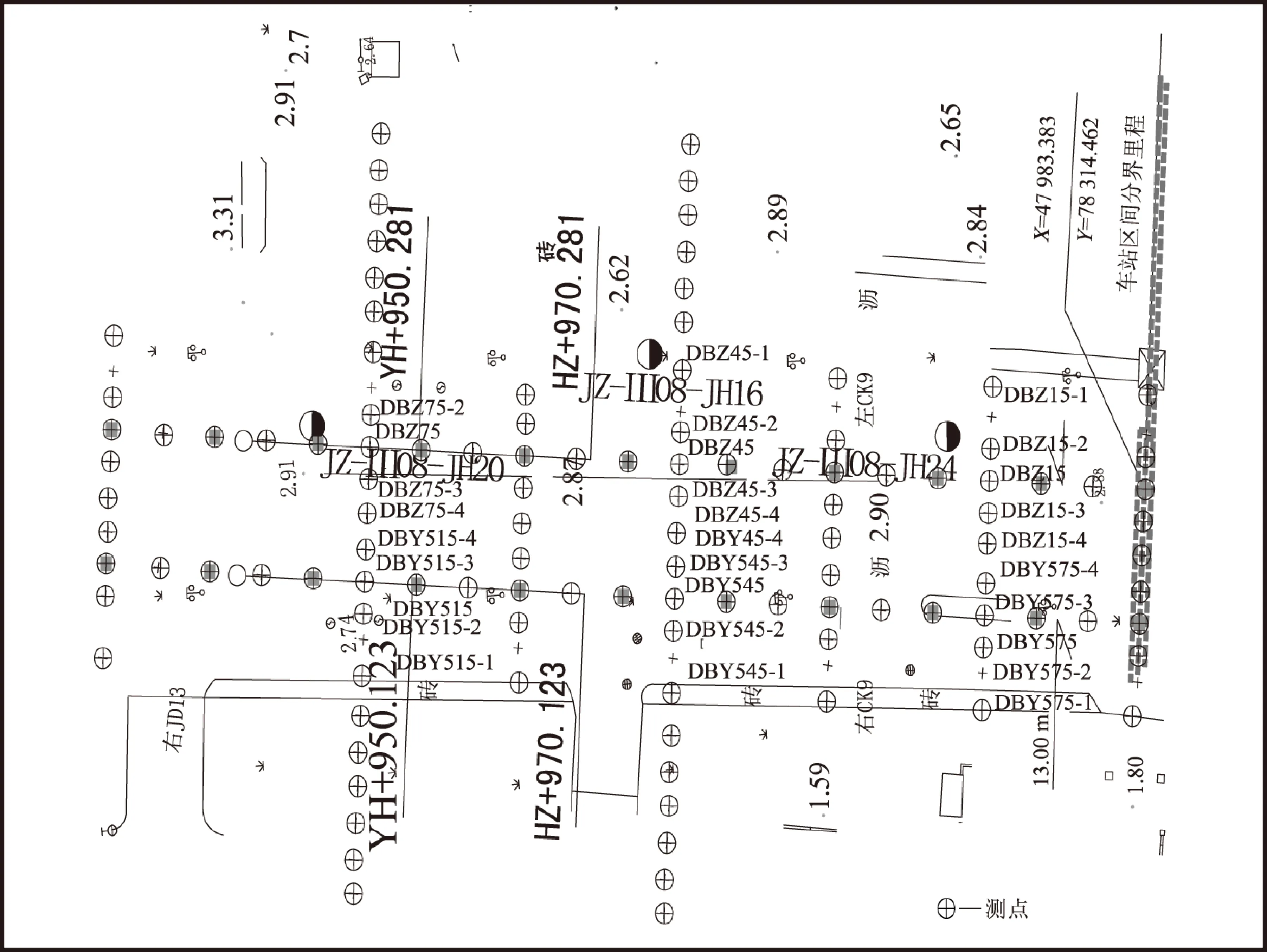
图2 地表沉降测点布置示意图
隧道内径为5.5 m,外径D=6.2 m,刀盘直径D0=6.34 m,管片厚0.35 m,土体泊松比μ=0.3。施工现场注浆量V=1.82 m3/m,隧道盾尾空隙Gp=7 cm,隧道埋深H=15 m。
1)理论注浆量(α取1.6):
V′=V/α=1.82÷1.6=1.14 (m3/m)。
2)地层损失参数(采用非等量径向土体变形模式):
3)地表沉降。采用地层损失非均匀分布模型,将ga代入式(16)计算的理论值和现场实测值如图3所示。
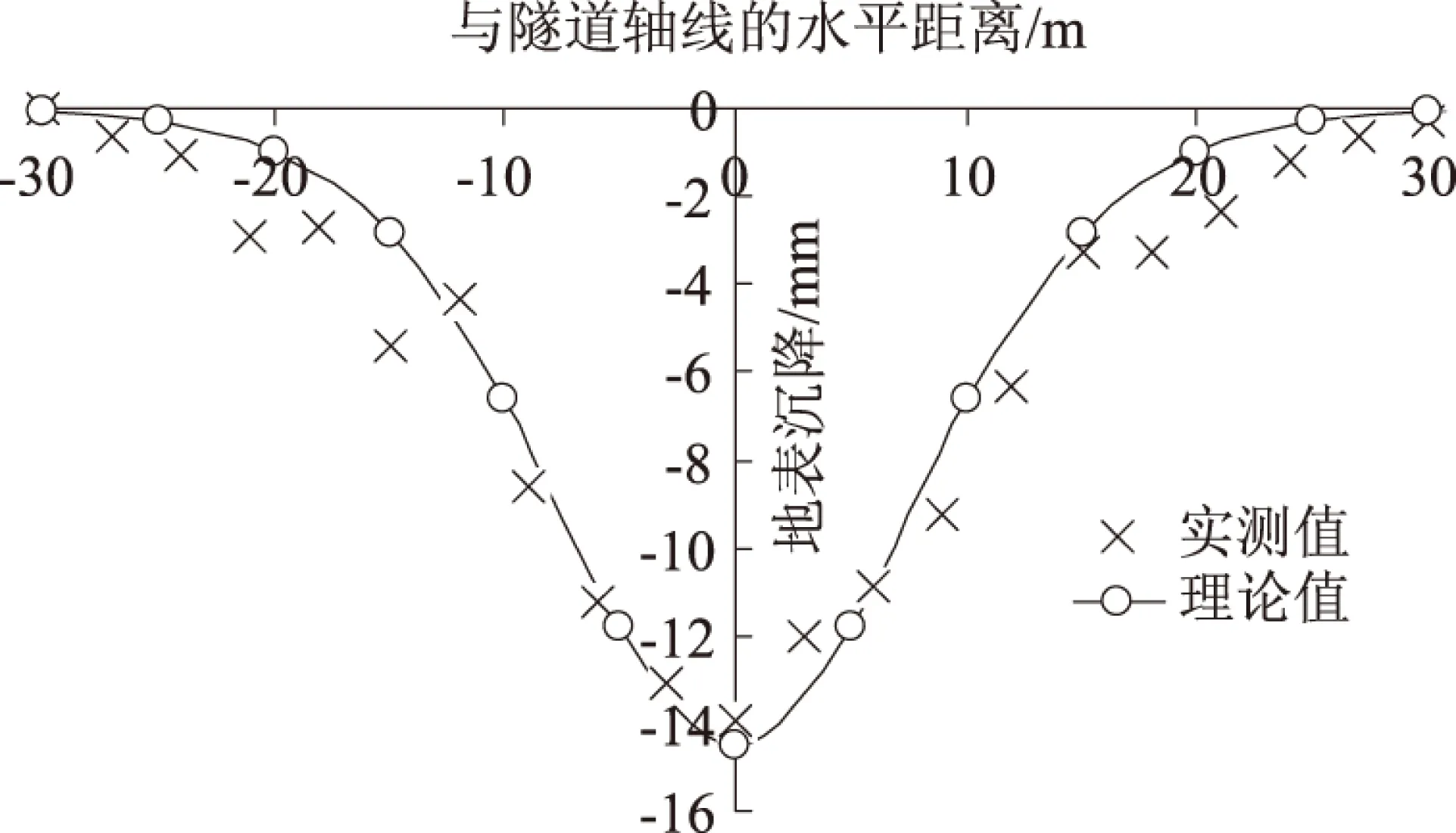
图3 地表沉降理论计算值与实测值比较
由图3可知,理论计算值与实测值取得了比较一致的结果,表明α取1.6是合适的(如果不一致,则调节α值使两者一致)。因沉降值偏大,现场注浆量1.82 m3/m并不是最佳注浆量。为求其在此地质条件下的最佳注浆量,由公式(16)和(17)计算的不同注浆量下的地表沉降如图4所示。地表沉降最大值与注浆量的关系如图5所示。

图4 不同注浆量下的地表沉降
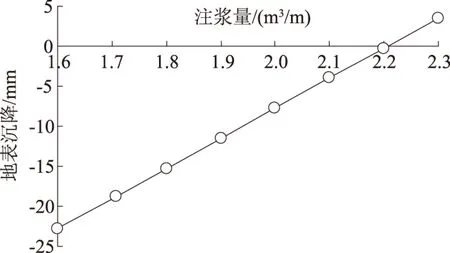
图5 地表沉降与注浆量的关系
由图4—5可知,地表沉降最大值与注浆量之间基本呈线性关系,注浆量越大,地表沉降越小。两者线性关系将给施工反分析提供很大的方便,施工时可以根据现场地表的隆沉情况对注浆量进行及时调整。如本算例,由以上分析可知,当注浆量取2.21 m3/m 时沉降量最小,其为施工最佳注浆量。
3 结 语
1)从施工安全的角度分析了土体临塑状态和极限状态下注浆压力的合理范围,引入安全系数,其大小可用于判断在一定土质条件下施工的安全状况,并从施工安全的角度提出了最优注浆压力的确定方法。
2)通过地层损失参数ga建立了地表沉降和理论注浆量的函数关系,在实际工程中可根据实际注浆量的大小和施工现场地表沉降实测数据反演得到合适的注浆参数α,再根据地表位移和注浆量基本呈线性关系这一结论,提出以控制沉降为目标的合理注浆量的确定方法。
3)本文为定量分析盾构施工土体变形与施工参数的关系提供了一种简便的方法。
[1]刘欢,韩娟.新建盾构隧道下穿施工对既有矿山法隧道的影响[J].华北水利水电大学学报(自然科学版),2015,36(5):76-80.
[2]薛晓辉,宿钟鸣,孙志杰.基于地层损失理论的盾构隧道沉降分析及控制措施研究[J].科学技术与工程,2013,13(32):9569-9573.
[3]孙闯,张建俊,刘家顺,等.盾构隧道壁后注浆压力对地表沉降的影响分析[J].长江科学院院报,2012,29(11):68-72.
[4]刘健,张载松,韩烨,等.考虑黏度时变性的水泥浆液盾构壁后注浆扩散规律及管片压力模型的试验研究[J]. 岩土力学,2015,36(2):361-368.
[5]朱才辉,李宁,柳厚祥,等.盾构施工工艺诱发地表沉降规律浅析[J].岩土力学,2011,31(1):158-164.
[6]Verruijt A,Booker J R.Surface settlements due to deformation of a tunnel in an elastic half plane[J].Géotechnique,1996,46(4):753-756.
[7]Lee K M,Rowe R K,Lo K Y.Subsidence owing to tunneling I:Estimating the gap parameter[J].Canadian Geotechnical Journal,1992,29(6):929-940.
[8]Loganathan N,Poulos H G,Xu K J.Ground and pile-group responses due to tunnelling[J].Soils and Foundations,2001,41(1):57-67.
[9]Chi S Y,Chern J C,Lin C C.Optimized back-analysis for tunneling-induced ground movement using equivalent ground loss model[J].Tunnelling and Underground Space Technology,2001,16(3):159-165.
[10]Park K H.Analytical solution for tunnelling-induced ground movement in clays[J].Tunnelling and Underground Space Technology,2005,20(3):249-261.
[11]林存刚,夏唐代,梁荣柱,等.盾构掘进地面沉降虚拟镜像算法[J].岩土工程学报,2014,36(8):1348-1446.
[12]黎春林.盾构施工固结沉降有限元分析[J].华北水利水电学院学报,2011,32(3):72-77.
[13]苟长飞,叶飞,张金龙,等.盾构隧道同步注浆充填压力环向分布模型[J].岩土工程学报,2013,35(3):590-598.
[14]叶飞,苟长飞, 陈治,等.盾构隧道同步注浆引起的地表变形分析[J].岩土工程学报,2014,36(4):618-624.
[15]邱明明,杨果林,姜安龙.盾构隧道同步注浆的压力分布及其影响因素[J].深圳大学学报理工版,2015,32(2):162-171.
[16]任青文,张宏朝.关于芬纳公式的修订[J].河海大学学报,2001,29(6):109-111.
[17]Loganathan N,Poulos H G.Analytical prediction for tunneling-induced ground movements in clays[J].Journal of Geotechnical and Geoenvironmental Engineering,1998,124(9):846-856.
[18]Sagaseta C.Analysis of undrained soil deformation due to ground loss[J].Géotechnique,1987,37(3):301-320.
[19]魏纲.盾构隧道施工引起的土体损失率取值及分布研究[J].岩土工程学报,2010,32(9):1354-1361.
(责任编辑:乔翠平)
The Simplified Algorithm of Reasonable Value of the Grouting Parameters during Shield Tunneling
LI Chunlin, SUN Yuyong, CHEN Jing
(Institute of Civil and Architectural Engineering, Tongling University, Tongling 244000, China)
During shield tunneling, the soil deformation around tunnel appears because of stress disturbance, the value of soil deformation is closely related to the grouting parameter. To analyze the influence of shield tunneling on the soil strength and deformation around the tunnel, the reasonable range of the grouting pressure was investigated based on the criteria of strength failure for soils, and the method determining the optimal grouting pressure was proposed from the aspect of the construction safety. Afterwards, the relationship between the grouting amount and the ground surface settlement was analyzed by virtual image technique, by comparing with the field observational data, the conclusion was drawn that the linearly relationship existed between the grouting amount and the ground surface settlement. On this basis, a simplified calculating method determining the optimal grouting amount was proposed with the objective of controlling the settlement.
shield tunnel; grouting pressure; grouting amount; ground surface settlement
2015-12-17
安徽省自然科学基金项目(1408085ME98,1608085ME103);安徽省高校自然科学研究项目(KJ2015A255,KJ2015A176)。
黎春林(1971—),男,安徽安庆人,副教授,博士,主要从事岩土工程方面的研究。E-mail:lichunlin111@126.com。 孙玉永(1980—),男,河南新乡人,副教授,博士,主要从事隧道和基坑工程方面的研究。E-mail:sunyuyong2@126.com。 陈静(1984—),女,安徽宣城人,讲师,博士,主要从事岩土工程方面的研究。E-mail:258018337@qq.com。
10.3969/j.issn.1002-5634.2016.02.012
TV543;TU472
A
1002-5634(2016)02-0067-06
