有风险偏好的区间直觉模糊多属性的意见集中排序法

徐 婷，成央金

（湘潭大学 数学与计算科学学院，湖南 湘潭 411105）

有风险偏好的区间直觉模糊多属性的意见集中排序法

徐 婷，成央金

（湘潭大学 数学与计算科学学院，湖南 湘潭 411105）

针对属性值为区间直觉模糊数的多属性群决策问题，考虑决策者风险偏好和属性权重不完全确定的情况，提出一种新的意见集中排序法。首先根据定义的得分函数对决策矩阵中的评价值比较大小，进而对方案排成线性序；然后基于新的排序方法，建立模型获得属性权重值，并利用加权平均算子对方案集结，得到排序方案。最后，通过数值实例验证该方法的可行性。

风险偏好；区间直觉模糊数；多属性决策；意见集中排序；得分函数

0 引言

L. A. Zadeh[1]在1965年提出模糊集的概念后，模糊集理论就得到了许多专家学者的关注，并应用到各个领域。因为模糊集理论只考虑了决策者满意和不满意2种状态，而没有考虑决策者的犹豫程度，所以随着社会的发展，模糊集理论不能完全解决一些不确定的问题。1986年，K. T. Atanassov[2]提出了直觉模糊集理论，该理论对模糊集理论进行了拓展与延伸，并从隶属度、非隶属度和犹豫度3个方面同时考虑事物的不确定性，因此它能更加准确地表示决策者的不确定性。1989年，K. T. Atanassov等[3-4]进一步完善了直觉模糊集，提出区间直觉模糊集理论，并定义了区间直觉模糊集的基本运算法则。之后，一些专家学者对完善区间直觉模糊集理论作出了巨大的贡献。徐泽水等[5-6]于2007年定义了区间直觉模糊数的加权几何集成算子和区间直觉模糊加权平均算子。以上这些丰硕成果为研究决策问题奠定了基础，其中文献[7-8]对直觉模糊集理论及其应用作了系统的研究；文献[9-15]研究了针对属性值为区间直觉模糊数的多属性决策问题；文献[16-19]研究了属性值为区间直觉模糊数且属性权重未知的多属性决策问题。

在他人研究的基础上，为解决属性权重不完全确定的决策者有风险偏好的区间直觉模糊的多属性群决策问题，本文提出了一种新的方法：意见集中排序法，它包括评分法和Blin法。根据决策者的风险偏好值和定义的得分函数对属性值为区间直觉模糊数进行排序，进而得到方案的线性序；然后分别采用评分法和Blin法建立多目标线性规划模型，求解出属性权重值并利用区间直觉模糊数加权平均算子获得各方案的综合属性值，得到排序方案。

1 预备知识

本章将简要介绍直觉模糊集的概念、区间直觉模糊集的概念及其运算，含决策者风险偏好参数的得分函数等基础知识。

K. T.Atanassov[2]首次对模糊集进行推广，提出了直觉模糊集的概念，并给出以下定义。

2 区间直觉模糊多属性决策问题的意见集中排序法

利用区间直觉模糊数加权平均算子，对决策者的区间直觉模糊决策矩阵的属性值进行集结，得到决策方案Ai(i=1, 2, …,n)关于属性Cj(j=1, 2, …,m)的综合属性区间直觉模糊数

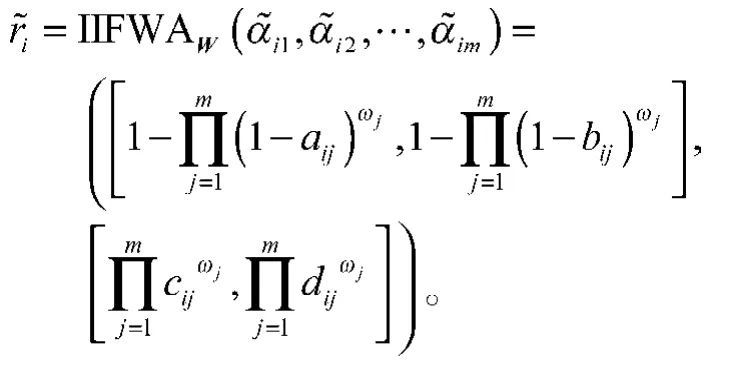
显然，综合属性区间直觉模糊数 越大，它对应的方案Ai就越优。如上所述，在属性权重已知的情况下易知方案Ai的优劣性。但在很多实际问题中，决策者往往只知道属性权重的取值范围，在这种情况下，需要事先确定属性权重。下面介绍2种方法求解属性权重值。

2.1 区间直觉模糊集中的评分法

由于Borda数越大，其对应的方案就越优，为了得到合理的权重向量，属性权重向量W的选择应该使加权Borda 数越大越好，为此建立如下多目标优化模型：

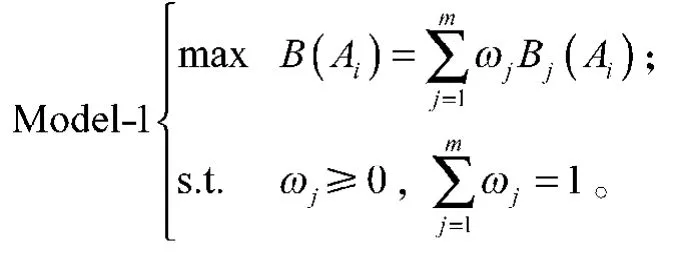
为了求解上述多目标规划，并考虑到所有目标函数是公平竞争的，没有任何偏好关系。于是，把上述多目标规划模型转化为单目标规划模型：

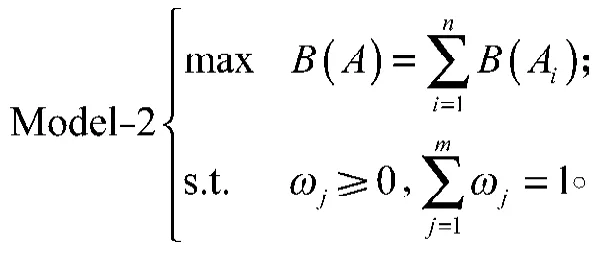
若属性权重信息完全未知，则只需求解Model-2即可。如果属性权重信息不完全确定，但已知取值范围，则只需在Model-2的限制条件中添加属性权重的取值范围，即得到以下规划模型：

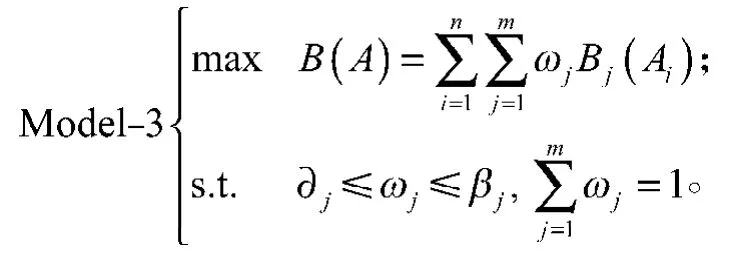
根据Model-3求解出属性权重W=(1,2, …,m)。

2.2 区间直觉模糊集中的Blin法

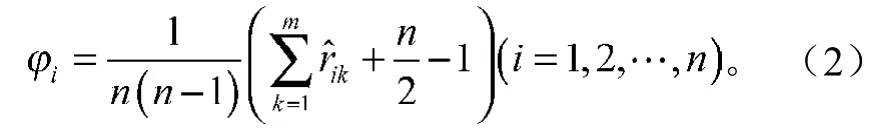
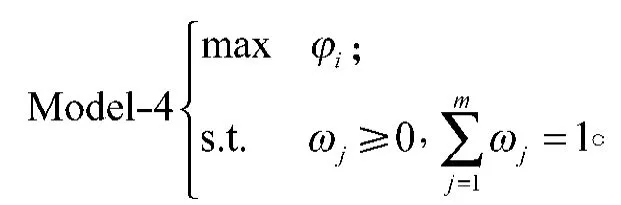
为了求解上述多目标规划，并考虑到所有目标函数是公平竞争的，没有任何偏好关系。于是把上述多目标规划模型转化为单目标规划模型：

若属性权重信息完全未知，则只需求解Model-5即可。如果属性权重信息不完全确定，但已知取值范围，则只需在Model-5的限制条件中添加属性权重的取值范围，即得到以下规划模型：

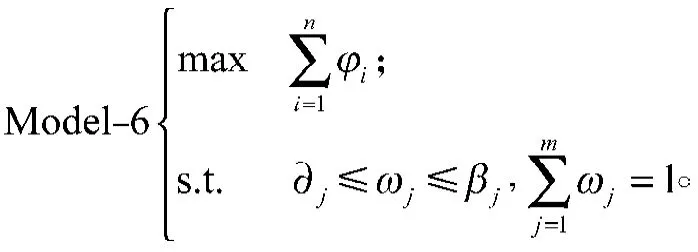
根据Model-6求解出属性权重W=(1,2, …,m)。

至此，得到2种有决策者风险偏好的区间直觉模糊数的多属性决策方法，具体算法如下。

算法1

3 实例分析

例1 考虑某风险投资公司选择企业进行项目投资，设有3家企业A1,A2,A3被选取，3个评价属性C1,C2,C3（分别为风险分析、社会经济政治影响分析、环境影响分析）。假设每家企业在各属性下的评估信息经过统计分析后，得到区间直觉模糊决策矩阵

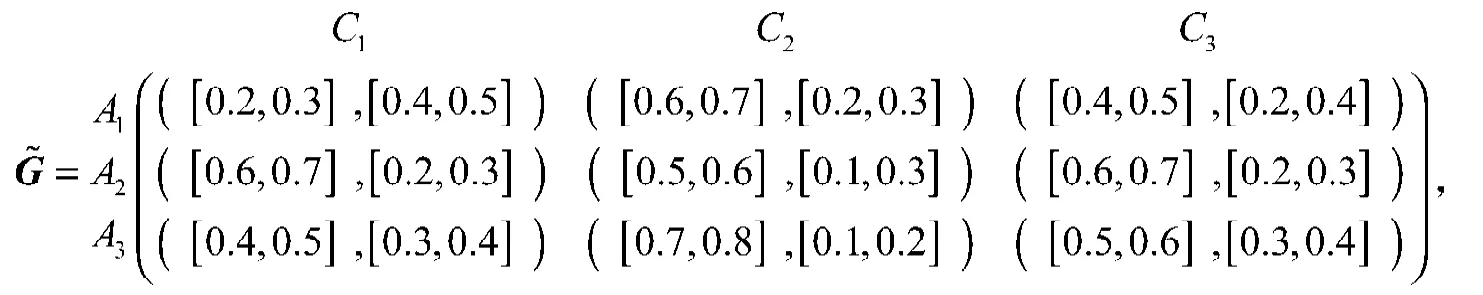
其中属性权重的信息不完全确定，它的取值范围为0.25≤1≤0.80，0.30≤2≤0.65，0.30≤3≤0.35，且1+2+3=1。而决策者属于风险冒险型，取=1。试根据本文的2种方法选择最佳企业进行投资。

4 结语

针对属性权重不完全确定，决策者有风险偏好，且属性值为区间直觉模糊数的多属性问题，提出了一种新的排序方法，该方法对模糊意见集中排序法进行延伸。对评分法给出了求解最大Borda数的多目标模型，对Blin法给出了求解最大优属度的多目标优化模型，从而获得相应的最优权重。利用加权平均算子，对区间直觉模糊信息进行集结，根据得分函数对方案排序择优。针对属性权重不完全确定的区间直觉模糊多属性问题，实例说明了决策方法的可行性。

[1]ZADEH L A. Fuzzy Sets[J]. Information and Control，1965，8(3)：338-353.

[2]ATANASSOV K T. Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems，1986，20(1)：87-96.

[3]ATANASSOV K T，GARGOV G. Interval Valued Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems，1989，31(3)：343-349.

[4]ATANASSOV K T. Operators over Interval-Valued Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems，1994，64(2)：159-174.

[5]徐泽水. 区间直觉模糊信息的集成方法及其在决策中的应用[J]. 控制与决策，2007，22(2)：215-219. XU Zeshui. Methods for Aggregating Interval-Valued Intuitionistic Fuzzy Information and Their Application to Decision Making[J]. Control and Decision，2007，22(2)：215-219.

[6]徐泽水，陈 剑. 一种基于区间直觉判断矩阵的群决策方法[J]. 系统工程理论与实践，2007，27(4)：126-133. XU Zeshui，Chen Jian. An Approach to Group Decision Making Based on Interval-Valued Intuitionistic Judgment Matrices[J]. Systems Engineering-Theory and Practice，2007，27(4)：126-133.

[7]徐泽水. 直觉模糊信息集成理论及应用[M]. 北京：科学出版社，2008：1-44. XU Zeshui. Intuitionistic Fuzzy Information Aggregation：Theory and Application[M]. Beijing：Science Press，2008：1-44.

[8]何 霞，刘卫锋. 一种有方案偏好的直觉模糊多属性决策方法[J]. 运筹与管理，2013，22(1)：36-40. HE Xia，LIU Weifeng. An Intuitionistic Fuzzy Multi-Attribute Decision-Making Method with Preference on Alternatives[J]. Operations Research and Management Science，2013，22(1)：36-40.

[9]王中兴，黄 娜，黄 帅. 基于决策者风险偏好的区间直觉模糊数多属性决策方法[J]. 广西科学，2014，21(2)：173-178. WANG Zhongxing，HUANG Na，HUANG Shuai. Multi-Criteria Decision-Making Method Based on Risk Attitude Under Interval-Valued Intuitionistic Fuzzy Environment[J]. Guangxi Science，2014，21(2)：173-178.

[10]NAYAGAM V L G，SIVARAMAN G. Ranking of Interval-Valued Intuitionistic Fuzzy Sets[J]. Applied Soft Computing，2011，11(4)：3368-3372.

[11]LIU B S，SHEN Y H，CHEN X H，et al. A Complex Multi-Attribute Large-Group PLS Decision-Making Method in theInterval-Valued Intuitionistic Fuzzy Environment[J]. Applied Mathematical Modelling，2014，38：4512-4527.

[12]WAN S P，DONG J Y. A Possibility Degree Method for Interval-Valued Intuitionistic Fuzzy Multi-Attribute Group Decision Making[J]. Journal of Computer and SystemSciences，2014，80：237-256.

[13]NAYAGAM V L G，MURALIKRISHNAN S，SIVARAMAN G. Multi-Criteria Decision-Making Method Based on Interval-Valued Intuitionistic Fuzzy Sets[J]. Expert System with Applications，2011，38：1464-1467.

[14]谭吉玉，朱传喜，张小芝，等. 基于TOPSIS的区间直觉模糊数排序法[J]. 控制与决策，2015，30(11)：2014-2018. TAN Jiyu，ZHU Chuanxi，ZHANG Xiaozhi，et al. Ranking Method of Interval-Valued Intuitionistic Fuzzy Numbers Based on TOPSIS[J]. Control and Decision，2015，30(11)：2014-2018.

[15]谢海斌，王中兴，谢国榕，等. 基于新精确函数的区间直觉模糊多属性决策方法[J]. 数学的实践与认识，2012，44(22)：182-188. XIE Haibin，WANG Zhongxing，XIE Guorong，et al. Multicriteria Fuzzy Decision-Making Method with Interval-Valued Intuitionistic Fuzzy Sets Based on a Novel Accuracy Function[J]. Mathematics in Practice and Theory，2012，42(22)：182-188.

[16]谢婉莹，成央金，杨 柳，等. 确定OWA算子权重的2个新模型[J]. 吉首大学学报（自然科学版），2015，36(6)：14-17. XIE Wanying，CHENG Yangjin，YANG Liu，et al. Two New Models for Weight Determination of OWA Operatio [J]. Journal of Jishou University（Natural Sciences Edition），2015，36(6)：14-17.

[17]陈志旺，杨 七，白 锌，等. 基于灰色关联求解权重未知的区间直觉模糊集多属性群决策[J]. 模糊系统与数学，2015，29(6)：64-75. CHEN Zhiwang，YANG Qi，BAI Xin，et al. Based on Grey Relational Analysis Method the Multiple Attribute Group Decision Making of Interval-Valued Intuitionistic Fuzzy Sets with Unknown Weights[J]. Fuzzy Systems and Mathematics，2015，29(6)：64-75.

[18]YE J. Multiple Attribute Group Decision-Making Methods with Completely Unknown Weights in Intuitionistic Fuzzy Setting and Interval-Valued Intuitionistic Fuzzy Setting[J]. Group Decision and Negotiation，2013，22(2)：173-188.

[19]XUE Y X，YOU J X，LAI X D，et al. An Interval-Valued Intuitionistic Fuzzy MABAC Approach for Material Selection with Incomplete Weight Information[J]. Applied Soft Computing，2016，38：703-713.

[20]QIU Z Y，DOSSKEY M G，KANG Y. Choosing Between Alternative Placement Strategies for Conservation Buffers Using Borda Count[J]. Landscape and Urban Planning，2016，153：66-73.

[21]金菊良，杨晓华，魏一鸣. 基于模糊优先关系矩阵的系统评价方法[J]. 系统工程理论方法应用，2005，14(4)：364-368. JIN Juliang，YANG Xiaohua，WEI Yiming. System Evaluation Method Based on Fuzzy Preferential Relation Matrix[J]. Systems Engineering-Theory Methodology Applications，2005，14(4)：364-368.

（责任编辑：邓光辉）

A Method of Attitudes Concentrated Order of Interval-Valued Intuitionistic Fuzzy Multiple Attributes with Risk Preference

XU Ting， CHENG Yangjin
（School of Mathematics and Computation Science，Xiangtan University，Xiangtan Hunan 411105，China）

In view of the fact that a multiple attribute group decision-making problem arises where attribute values are provided as interval-valued intuitionistic fuzzy numbers, a new met,hod of attitudes concentrated order has been proposed, taking into consideration the situations where the decision makers risk preferences and attribute weights are not completely determined. Firstly, a comparison has been made of the evaluation values in the decision matrix according to the defined score function, followed by an arrangement of the schemes in linear sequence. Secondly, the attribute weights can be obtained with a model built on the basis of this new ranking method, and an ultimate ordering scheme can be worked out by taking advantage of the weighted average operator to aggregate all the schemes. Finally, a numerical example is given to verify the feasibility of this method.

risk preference；interval-valued intuitionistic fuzzy number；multiple attribute decision making；attitudes concentrated order；score function

O223；C934

A

1673-9833(2016)06-0075-07

10.3969/j.issn.1673-9833.2016.06.014

2016-09-20

湖南省自然科学基金资助项目（14JJ2069）

徐 婷（1992-），女，湖南益阳人，湘潭大学硕士生，主要研究方向为不确定性优化理论及其应用，E-mail：1448057666@qq.com