基于Radon-Ambiguity变换的LFM信号时/频差快速联合估计

杨林森 张子敬 郭付阳

(西安电子科技大学 雷达信号处理国家重点实验室，西安 710071)

基于Radon-Ambiguity变换的LFM信号时/频差快速联合估计

杨林森 张子敬 郭付阳

(西安电子科技大学 雷达信号处理国家重点实验室，西安 710071)

提出了一种基于Radon-Ambiguity变换(Radon-Ambiguity Transform, RAT)的线性调频(Linear Frequency Modulated, LFM)信号时/频差快速联合估计的算法。根据LFM信号在多个不同角度上的RAT峰值位置建立一组以信号间时差和频差为未知量的方程组，求解方程组即可得到时/频差的估计值。对于存在噪声的信号，RAT误差会导致方程组不能直接求解，为了抑制噪声干扰，采用最小二乘法估计时/频差。本文算法无需计算二维平面上各点的模糊函数值，并且由于离散RAT可以通过快速傅里叶变换快速实现，具有所需运算量低的优点。仿真实验表明，相比于常见的基于模糊函数峰值搜索的时/频差估计算法，本文算法在保证时/频差估计精度的同时能够显著地提高运算效率。

Radon-Ambiguity变换；最小二乘法；时/频差；线性调频信号

引 言

对于两路信号间时差和频差的估计问题广泛地存在于雷达，声纳和导航的很多应用之中[1-4].在无源定位技术中，常常根据两路接收信号间的时差和频差对目标辐射源进行精确定位.双星时/频差定位是一种最常见的无源定位技术的应用，它利用两颗卫星接收同一地面辐射源的辐射信号，由于两颗卫星相对于该地面辐射源具有不同的距离和径向速度，因此卫星接收到的两路信号间存在时差和多普勒频差.由两路接收信号间的时差和频差可以确定出目标辐射源在空间中可能出现的区域范围，再结合地球表面方程，即可最终实现地面辐射源的精确定位，显然时/频差估计技术直接影响到最终的定位性能.模糊函数是估计信号间时/频差最常使用的工具[5]，模糊函数是一种在时间和频率二维平面上定义的广义相关.若两路信号间仅存在时差，利用时域相关即可有效地估计该时差，然而当两路信号间同时存在时差和频差时，时域相关显然无法满足时差和频差的同时估计，模糊函数作为时频二维平面上的广义相关，可以实现两路信号间时差和频差的同时估计.类似于由时域相关峰值估计时差的过程，利用两路信号间互模糊函数峰值位置也可以实现信号间时差和频差的估计.然而，计算二维模糊平面上各点的模糊函数值并搜索峰值意味着巨大的运算量，信号间的时/频差仅仅与模糊函数峰值点位置有关，为了寻找峰值而计算整个模糊平面上各点的函数值显然存在巨大的计算冗余.为此，研究人员提出了很多提高模糊函数峰值搜索效率的改进算法.文献[6]提出了先粗估计模糊函数峰值位置再精估计的思路，减少了很多不必要的计算.文献[7]根据多普勒频移一般远小于采样频率的特点，提出对两路信号的混合积信号先进行低通滤波再抽取处理过程，显著地减小了所处理信号的长度，从而降低了运算量.对于线性调频(Linear Frequency Modulated, LFM)信号，文献[8]根据其模糊函数图存在一条过峰值点、斜率为调频率的脊线的特点，将模糊函数二维峰值搜索转化为沿脊线的一维峰值搜索，从而显著地降低了时/频差估计所需的运算量.

分数阶傅里叶变换(fractional Fourier transform, FrFT)作为傅里叶变换的推广，广泛地应用于信号的检测以及参数估计等问题中[9-12].文献[13]中给出了离散FrFT基于快速傅里叶变换(Fast Fourier Transform, FFT)的快速实现方法，运算复杂度与FFT算法相当.Radon变换是一种沿直线积分的投影变换[14]，Radon-Ambiguity变换(Radon-Ambiguity Transform, RAT)将信号的模糊函数在模糊平面上进行Radon变换.文献[15]结合FrFT和模糊函数的性质，将RAT的定义式化简为基于若干次FrFT和傅里叶变换的形式，因此离散RAT可以通过若干次FFT快速实现，显著地降低了RAT所需的运算量.

本文提出了一种基于RAT的LFM信号时/频差快速联合估计算法.首先根据两路LFM信号在不同角度上RAT的峰值位置建立一组以时差和频差为未知量的方程组，求解方程组即可获得时差和频差估计值.对于受到噪声干扰的信号，RAT误差会导致方程组不能直接求解.为了抑制噪声的影响，采用最小二乘法求解时/频差.最后，通过理论分析和仿真实验，分别对比了本文算法和文献[8]提出的Radon-Ambiguity单切片(single slice of Radon-Ambiguity transform，SSRAT)时/频差估计算法所需的运算时间和估计精度.

1 模糊函数及Radon-Ambiguity变换

假设在噪声环境中存在时差和频差的两路LFM信号为

(1)

对于两路信号r1(t)和r2(t),其互模糊函数定义为[5]

(2)

若不考虑噪声影响,将式(1)代入式(2),可以得到LFM信号的互模糊函数

(3)

由式(3)可以看出,LFM信号互模糊函数存在一个峰值点(Δτ,Δf),并且在二维模糊平面上还存在一条过峰值点的脊线,脊线所对应的方程为

f=mτ+Δf-mΔτ．

(4)

RAT变换是对信号的模糊函数χ(τ,f)在二维模糊平面上做Radon投影变换[14]的结果．图1为RAT变换的示意图,图中τ轴和f轴分别为模糊平面的时延轴和多普勒频率轴,将τ轴逆时针旋转角度φ得到u轴,v轴垂直于u轴．信号在角度φ上的RAT定义为模糊函数χ(τ,f)沿着平行于v轴并且与u轴交于不同位置的直线PQ的积分变换,即

RAT(u,φ)=∫PQχ(τ,f)dv．

(5)

图1 RAT变换示意图

若根据式(5)计算RAT,则需先计算模糊函数在二维平面上各点的函数值,然后再对模糊函数沿不同的积分路径进行积分,需要巨大的运算量,不利于快速实现．文章[15]结合FrFT和模糊函数的性质,将信号的RAT化简为基于FrFT和傅里叶变换的等价形式:

(6)

式中:Rφ(r)为信号r(t)在角度φ上的FrFT．由于离散FrFT能够通过FFT快速实现[13],因此,根据式(6),离散RAT可以通过若干次FFT快速实现,能够显著地提高RAT的计算效率．

2 利用RAT估计LFM信号时/频差

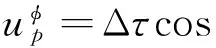
(7)

根据式(4),LFM信号的模糊函数存在一条过峰值点且斜率为调频率m的脊线．模糊函数上的主要能量都集中在脊线上,当φ=arctanm时,RAT的积分路径与LFM信号模糊函数的脊线平行,脊线上的所有点将投影聚焦于一点,产生一个极大的峰值,因此信号在角度φ=arctanm的RAT峰值具有很强的抗噪声性能,建立的方程式(7)具有较高的精度．然而,当φ≠arctanm时,RAT峰值点的产生过程没有积累的作用,RAT峰值点的位置估计易受到噪声的干扰,建立的方程式(7)易受噪声干扰而产生误差．因此,由两个不同角度的RAT峰值位置建立的方程组中至少存在一个易受噪声干扰方程,最终求解的时/频差估计值无法保证精度．为了抑制噪声对时/频差估计精度的影响,本文将选取多个不同角度进行RAT,利用多次观测来降低单次观测的误差对时/频差估计值的影响．

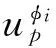
(8)

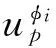
Ax=b．

(9)

(10)

将LFM信号在各角度的RAT峰值位置观测向量b代入式(10)即可得到时/频差的最小二乘估计．

本文提出的基于RAT的LFM信号时/频差快速联合估计算法的步骤可以总结如下:

1) 在区间[0,π)均匀选取M个角度,记为φi(i=1,…,M)．提前计算式(10)中的矩阵(ATA)-1AT．

4) 对于步骤3)中得到的乘积信号,计算其逆FFT,结果即为两路信号在角度φi上的RAT．

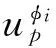
6) 利用式(10)直接计算两路LFM信号间时/频差的最小二乘解．

3 算法运算量分析

模糊函数是估计信号间时/频差最常用到的工具,为了提高模糊函数峰值搜索的运算效率,文献[8]提出了SSRAT算法．SSRAT算法利用LFM信号模糊函数在二维平面上存在一条过峰值脊线的特点,首先估计出LFM模糊函数脊线的位置,然后沿着脊线搜索模糊函数峰值,由文献[8]的结论可知SSRAT算法能够显著降低时/频差估计所需的运算量．下面我们将对比本文算法和SSRAT算法所需的运算量．

假设离散采样信号的长度为N,本文算法所需要的RAT角度个数为M．对于本文算法,由式(6)计算任意角度的RAT仅需计算两次FrFT和三次傅里叶变换,计算离散采样信号的FrFT和傅里叶变换都能够利用FFT快速实现,分别需要复乘次数约为3Nlog2N+N[13]和Nlog2N,则计算信号在M个角度的RAT所需的总复乘次数约为9MNlog2N+6MN．根据信号在M个角度上RAT的峰值位置,利用式(10)可直接求解时/频差的最小二乘解．式(10)中矩阵A的取值只与RAT角度有关,矩阵A可以认为是已知的,因此矩阵(ATA)-1AT也可以预先计算,在此不考虑其所需的运算量．将向量b代入式(10)计算信号时/频差的最小二乘解所需的复乘次数为2M．综上分析,本文算法的运算量约为9MNlog2N+6MN+2M．

考虑到实际问题中的离散采样信号长度N一般都会较大,而本文算法所需的RAT角度个数M一般小于102,因此M往往远远小于信号的长度N,即M≪N,则本文算法的运算量可以认为是O(Nlog2N),而SSRAT算法的运算量为O(N2)[8]．因此相比于SSRAT算法,本文算法的运算量更小,运算效率更高．

4 仿真实验

下面我们将通过仿真验证本文算法的性能,假设两路LFM信号带宽为50 kHz,调频率31.25 MHz/s,初始频率κ=0,采样频率为200 kHz,信号持续时间为1.6 ms,观测时间为2 ms,两路信号间的时差和频差分别为-10 μs和-3.2 kHz．

4.1 RAT角度搜索数量对本文算法性能的影响

图2(a)仿真了信号在不同角度上RAT峰值位置与该信号模糊函数峰值点在对应角度的u轴上投影位置的关系．为了避免不同的量纲对实验结果的影响,在仿真中对离散采样信号的时间和频率信息进行了去量纲处理[13]．图2(a)中的实线为该信号在[0,π)上各角度RAT峰值位置的仿真曲线,虚线为该信号模糊函数峰值点在各对应角度u轴上投影位置理论曲线．对于离散采样信号,其RAT也是离散的,若选取的两个RAT角度足够接近,会使得不同角度的RAT峰值位置落入同一个离散分辨单元而无法区分,因此图2(a)中的RAT峰值位置变化仿真曲线是一条存在阶跃的曲线．可以看出,图2(a)中的实线和虚线位置相互吻合,验证了LFM信号在任意角度上RAT的峰值位置等于其互模糊函数峰值点在该角度所对应u轴上的投影位置．

图2(b)和(c)分别仿真了在输入信噪比为10 dB时,本文算法时差和频差估计均方根误差随RAT角度数量的变化曲线．由图2(b)和(c)中的曲线可以看出:当RAT角度数量小于30时,本文算法时/频差估计均方根误差随RAT角度数量增加而迅速减小;当RAT角度数量大于60时,本文算法的时/频差估计均方根误差趋于稳定,基本不再随RAT角度数量的增加而降低．这是因为当RAT角度数量较小时,RAT角度数量的增加使得观测样本增加,有利于抑制单次观测误差对时/频差估计精度的影响,然而当RAT角度数量已经较大时,再增加RAT角度数量会导致相邻角度间的差距过小,由前面的分析可知,对于差距较小的两个角度,根据式(7)得到的两个方程会接近线性相关,进而求解的时/频差估计值易受RAT峰值位置估计误差的影响,因此当RAT角度数量增加到一定程度时,本文算法时/频差估计精度不会再随RAT角度数量增加而提高．考虑到RAT角度数量会影响本文算法所需运算量,为了平衡估计精度和所需的运算量,本文算法RAT角度数应在30～60选择．

4.2 本文算法和几种常见算法的性能比较

图3仿真了本文算法和SSRAT算法时/频差估计均方根误差随输入信噪比的变化曲线.为了得到不同算法时差和频差估计的均方根误差，对于图3中的每一个信噪比，我们分别进行了500次蒙特卡洛仿真，并且和克拉美-罗界[6]进行了比较.由图3(a)和(b)可以看出，两种不同算法的时/频差估计均方根误差曲线基本重合，并且随信噪比的提高两种不同算法的时/频差估计均方根误差曲线都不断减小且接近克拉美-罗界，两种算法都能够得到较高的时/频差估计精度.

图3 不同算法的时/频差估计均方误根差随信噪比的变化曲线

图4仿真了本文算法和SSRAT算法所需的运算时间随信号长度变化的仿真曲线.在该仿真中，信号长度在变化，其余参数与之前相同.根据4.1节中的仿真结果可知，为了同时满足较高的时/频差估计精度和较小的运算量，本文算法所需的RAT角度数量应在区间选择，因此图4针对本文算法的仿真仅选取了RAT角度数量为30和60的两种情况.对比图4中的3条不同曲线可以看出：在相同的信号参数条件下，本文算法在RAT角度数量为30和60时所需的运算时间都明显小于SSRAT算法所需要的运算时间；另外，本文算法在RAT角度数为30时所需的运算时间略小于RAT角度数为60时所需的运算时间.

结合图3和图4的仿真结果可知，本文算法和SSRAT算法的时/频差估计精度基本相同，都能实现时/频差的精确估计，但是本文算法能够显著降低运算时间，运算效率具有明显的优势.

图4 不同算法时/频差估计运算时间比较

5 结 论

对于两路存在时差和频差的LFM信号，本文提出了一种基于RAT的时/频差快速联合估计算法.根据LFM信号在任意一个角度上RAT的峰值位置能够得到一个以信号间时差和频差为未知量的二元方程，选取多个不同的角度能够建立一组二元方程组，求解方程组即可得到时/频差的估计值.对于存在噪声干扰的信号，其RAT误差会导致得到的方程组不能直接求解.为了抑制噪声的影响，本文算法采用最小二乘法实现时/频差的估计.本文算法无需计算二维平面上各点的模糊函数值，并且存在基于FFT的快速实现方法，由理论分析可知，本文算法所需的运算量远小于SSRAT算法，同时实验仿真验证了，在相同条件下，本文算法和SSRAT算法时/频差估计精度相同，都能够获得较高的时/频差估计精度，然而本文算法所需的运算时间明显小于SSRAT算法.由于时/频差估计技术是无源定位的关键技术，本文提出的时/频差估计算法同时具有估计精度高和运算复杂度低的特点，具有一定的实际应用价值，特别适合于对时/频差估计的速度和精度都有要求的实时处理问题，例如双星利用时/频差对雷达或通信基站的定位问题.

[1] KIM Y H, KIM D G, KIM H N. Two-step estimator for moving-emitter geolocation using time difference of arrival/frequency-difference of arrival measurements[J]. IET Radar, Sonar & Navigation, 2015, 9(7): 881-887.[2] 李昕. 基于双通道DFRFT互谱法的Chirp信号时延估计[J]. 电子学报, 2014, 42(6): 1068-1073.

LI X. Time delay estimation of Chirp signals based on doubled-channel DFRFT cross-spectrum[J]. Acta Electronica Sinica, 2014, 42(6): 1068-1073. (in Chinese)

[3] MUSICKI D, KAUNE R, KOCH W. Mobile emitter geolocation and tracking using TDOA and FDOA measurements[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1863-1874.

[4] 朱文涛, 苏涛, 杨涛, 等. 低信噪比下线性调频连续波信号的参数估计[J]. 电波科学学报, 2013, 28(6): 1158-1164.

ZHU W T, SU T and YANG T, et al. Parameter estimation of linear frequency modulated continuous wave signal in low SNR[J]. Chinese Journal of Radio Science, 2013, 28(6): 1158-1164.

[5] STEIN S. Differential delay/Doppler ML estimation with unknown signals[J]. IEEE Transactions on Acoustic, Speech, and Signal Processing, 1993, 41(8): 2717-2719.

[6] STEIN S. Algorithms for Ambiguity function processing[J]. IEEE Transactions on Acoustic, Speech, and Signal Processing, 1981, 29(3): 588-599.

[7] TOLIMIERI R, WINOGRAD S. Computing the Ambiguity surface[J]. IEEE Transactions on Acoustic, Speech, and Signal Processing, 1985, 33(4): 1239-1245.

[8] SHARIF M R, ABEYSEKERA S S. Efficient wideband signal parameter estimation using a Radon-Ambiguity transform slice[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 673-688.

[9] 刘锋, 徐会法, 陶然, 等. 分数阶Fourier域多分量LFM信号间的分辨研究[J]. 中国科学(信息科学), 2012, 42(2): 136-148.

LIU F, XU H F, TAO R, et al. Research on resolution among multi-component LFM signals in the fractional Fourier domain[J]. Science China (Information Science), 2012, 42(2): 136-148. (in Chinese)

[10] 战立晓, 汤子跃, 朱振波. 基于分数阶傅里叶变换的加速微弱目标检测与估计[J]. 电波科学学报, 2013, 28(2): 296-304.

ZHAN L X, Tang Z Y, ZHU Z B. FRFT based detection and estimation of accelerating weak target[J]. Chinese Journal of Radio Science, 2013, 28(2): 296-304. (in Chinese)

[11] SEJDIC E, DJUROVIC I, STANKOVIC L. Fractional Fourier transform as a signal processing tool: An overview of recent developments[J]. Signal Processing, 2010, 91(6): 1351-1369.

[12] OONINCX P J. Joint time-frequency offset detection using the fractional Fourier transform[J]. Signal Processing, 2008, 88: 2936-2942.

[13] OZAKTAS H M, ARIKAN O, KUTAY M A, et al. Digital computation of the fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 1996, 44(9): 2141-2150.

[14] WOOD J C, BARRY D T. Tomographic time-frequency analysis and its application toward time-varying filtering and adaptive kernel design for multicomponent linear-FM signals[J]. IEEE Transactions on Signal Processing, 1994, 42(8), pp: 2094-2104

[15] YANG L S, ZHANG Z J, GUO F Y. Fast algorithm for Radon-Ambiguity transform[J]. IET Radar, Sonar & Navigation, 2016, 10(3), pp: 553-559

[16] 张贤达. 矩阵分析与应用[M]. 北京:清华大学出版社, 2004: 71-96.

ZHANG X D. Matrix analysis and applications[M]. Beijing: Tsinghua University Press, 2004: 71-96 (in Chinese)

Joint time-frequency offset estimation for LFM signals based on the Radon-Ambiguity transform

YANG Linsen, ZHANG Zijing, GUO Fuyang

(NationalLaboratoryofRadarSignalProcessing,XidianUniversity,Xi’an710071,China)

A fast method for joint estimation of the time-frequency offset for linear frequency modulated signals based on the Radon-Ambiguity transform (RAT) is proposed in this paper. According to peak positions of the RAT of a LFM signal on different angles, a set of equations with the time-frequency offset as the unknowns can be established and the time-frequency offset can be estimated by solving the equations. For signals disturbed by noise, errors of the RAT will cause the equations having no solutions. In order to eliminate the noise, the least square method is used to estimate the time-frequency offset. Because the proposed algorithm does not need to calculate the value of each point on the 2-D Ambiguity plane and the RAT for sampled signals can be realized rapidly by several processes of the fast Fourier transform, the proposed method has advantage of low computational cost. Simulation results show that the proposed algorithm can ensure the accuracy of the estimation of the time-frequency offset as well as is computationally efficient compared with common methods based on peak searching of the Ambiguity function.

Radon-Ambiguity transform; Least square method; Time-frequency offset; LFM

10.13443/j.cjors.20160916

2016-09-16

国家自然科学基金(No.61571349, No.61201325)；国家留学基金资助项目

TN911.72

A

1005-0388(2016)06-0-0

杨林森 (1988-)，男，陕西人，博士研究生，研究方向为时频分析、雷达信号处理.

张子敬 (1967-)，男，陕西人，教授，博士生导师，研究方向为无源定位、雷达信号处理.

郭付阳 (1991-)，男，江西人，博士研究生，研究方向为时频分析、雷达信号处理.

杨林森, 张子敬, 郭付阳. 基于Radon-Ambiguity变换的LFM信号时/频差快速联合估计[J]. 电波科学学报，2016,31(6)：页码.

YANG L S, ZHANG Z J, GUO F Y. Joint time-frequency offset estimation for LFM signals based on the Radon-Ambiguity transform[J]. Chinese journal of radio science，2016,31(6)：页码.(in Chinese). DOI: 10.13443/j.cjors.20160916

联系人： 杨林森 E-mail：yls198802@163.com

DOI 10.13443/j.cjors.20160916