二次函数零点式在圆锥曲线中的应用



二次函数零点式在圆锥曲线中的应用

梁昌金

(安徽省寿县第一中学,232200)

直线与圆锥曲线的位置关系类高考试题，基本与一元二次函数及韦达定理形影不离,这样就使得问题解决具有模式化.笔者时常在思考,能否回避韦达定理呢?在复习二次函数形式时,二次函数的零点式f(x)=a(x-x1)(x-x2)(a≠0,x1,x2为函数y=f(x)与x轴交点的横坐标,亦是方程f(x)=0的两个实数根)给笔者以启发.以下就是笔者运用零点式解决圆锥曲线问题时的一点尝试.

(1)求椭圆E的方程;

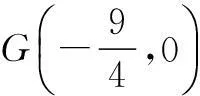
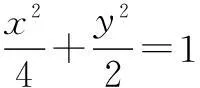
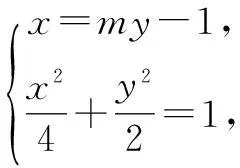
(m2+2)y2-2my-3=0.

设A(x1,y1),B(x2,y2),则y1,y2是方程(m2+2)y2-2my-3=0的两个根,于是有

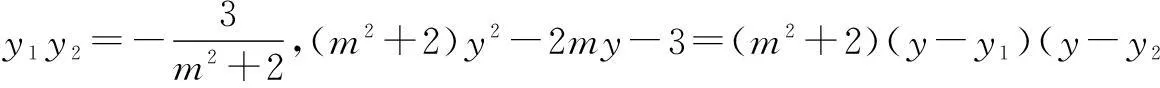
①

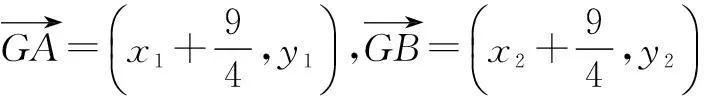
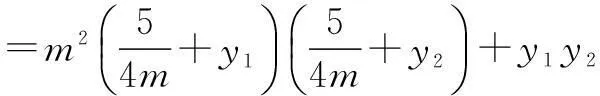
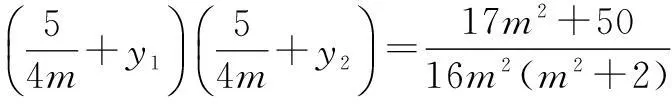
代入上式，得

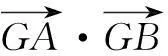
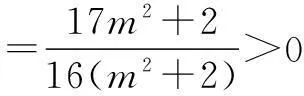
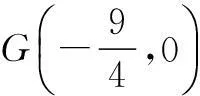
例2(2010年湖北高考题)已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.

(1)求曲线C的方程;

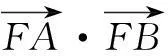
解(1)曲线C的方程为y2=4x(x>0)(过程略).

(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1,y1),B(x2,y2).

设l的方程为x=ty+m.

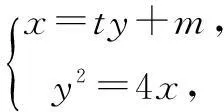
y2-4ty-4m=0,Δ=16(m+t2)>0.

因为y1,y2是方程的根,所以y1y2=-4m,

y2-4ty-4m=(y-y1)(y-y2).

②

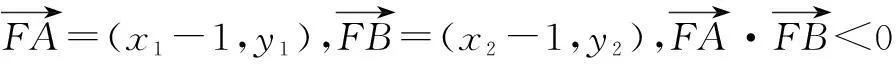
(x1-1)(x2-1)+y1y2

=(ty1+m-1)(ty2+m-1)+y1y2

+y1y2

<0.

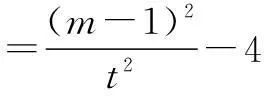
于是得到m2-6m+1<4t2.

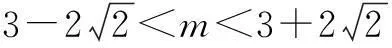
例3(2008年陕西高考题)如图1，已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过点M作x轴的垂线交C于点N.

(1)证明:抛物线C在点N处的切线与AB平行;

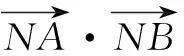
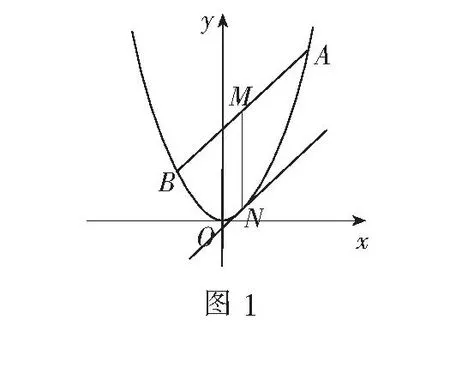
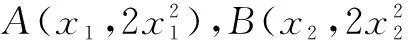
把y=kx+2代入y=2x2，得

2x2-kx-2=0.

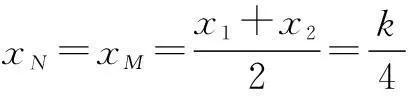
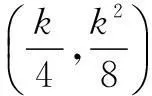
设抛物线在点N处的切线l的方程为

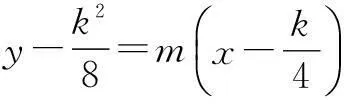
将y=2x2代入上式，得

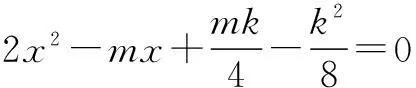
∵直线l与抛物线C相切,

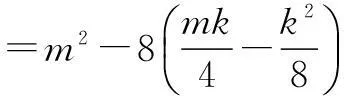
=m2-2mk+k2=(m-k)2=0,

∴m=k.即l∥AB.

烂眼阿根不但好色，而且好酒；年轻时两斤老酒不在话下，上了年纪之后，喝到半斤光景就很有些醉意了，但从小醉到大醉的间距特别长，他就是再喝半斤也是如此。这天烂眼阿根喝下半瓶酒后，男人婆就把他的酒瓶藏了起来；烂眼阿根起身去厨房找时，找到的却是男人婆早已准备好的，灌了甲胺磷的毒酒。烂眼阿根这时候已经很有些醉意了，居然喝不出酒中的怪味儿，他把那半瓶毒酒全喝了。

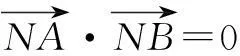
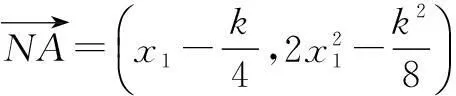
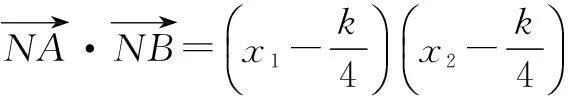
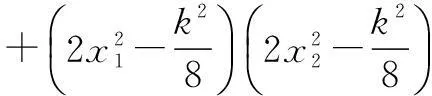
由(1)知x1,x2是方程2x2-kx-2=0的根,所以

2x2-kx-2=2(x-x1)(x-x2).

③

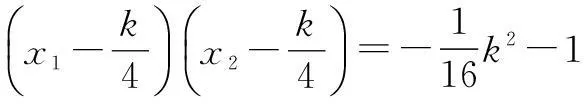
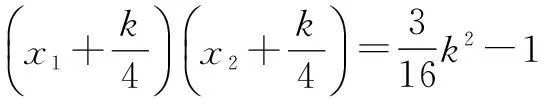
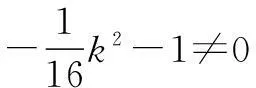
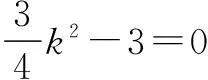
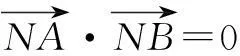
例4(2007年山东高考题)已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.

(1)求椭圆C的标准方程;

(2)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.

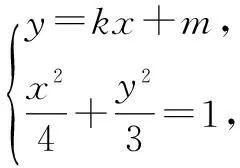
(3+4k2)x2+8mkx+4(m2-3)=0,

Δ=(8mk)2-16(3+4k2)(m2-3)

=48(3+4k2-m2).

设A(x1,y1),B(x2,y2),则x1,x2是方程的根,所以

(3+4k2)x2+8mkx+4(m2-3)

=(3+4k2)(x-x1)(x-x2).

④

因为以AB为直径的圆过椭圆的右焦点D(2,0),所以

=(x1-2)(x2-2)+y1y2

=(x1-2)(x2-2)

+(kx1+m)(kx2+m)

=(x1-2)(x2-2)

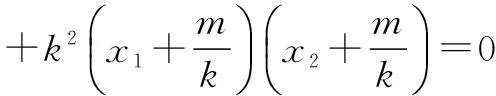
在④ 式中令x=2,得

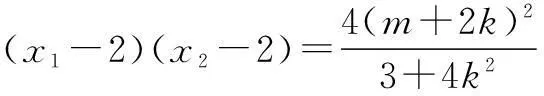
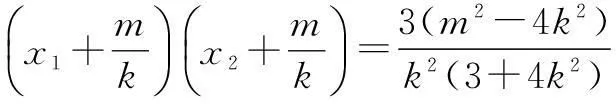
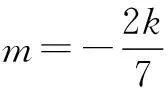
当m=-2k时,l的方程为y=k(x-2),直线过定点(2,0),与已知矛盾;

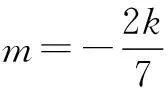
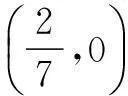
数学的学习离不开思考,方法无穷无尽,只要我们善于思考,在继承的基础上大胆创新,就能拓宽解题视野,活跃数学思维能力,充分享受数学.

○解题思路与方法○