基于纤维模型的梁桥材料非线性研究*
2016-03-04杨国俊郝宪武段瑞芳李子青
杨国俊 郝宪武 段瑞芳 李子青
(长安大学公路学院1) 西安 710064) (陕西交通职业技术学院2) 西安 710018)
基于纤维模型的梁桥材料非线性研究*
杨国俊1)郝宪武1)段瑞芳2)李子青1)
(长安大学公路学院1)西安710064)(陕西交通职业技术学院2)西安710018)
摘要:为了提高工程结构非线性的计算精度,研究了OpenSEES程序中的纤维模型,以多梁式简支T梁桥为背景,建立体系的纤维模型,通过偏载、中载、均匀加载三种方式,分析各片主梁的材料非线性变化过程.在偏载加载方式下,数值模拟的各主梁荷载-位移,以及荷载-钢筋应力曲线分别与破坏性试验数据进行了对比分析.结果表明,模拟的误差很小,两者结果相吻合,说明OpenSEES有限元的纤维模型分析非线性具有更高的精度和优越性.
关键词:桥梁工程;纤维模型;材料非线性;多梁式钢筋混凝土;本构关系
杨国俊(1988- ):男,博士生,主要研究领域为桥梁桥梁结构及结构分析理论
*中央高校基本科研业务费资助 (批准号:2013G1211010)
0引言
大量的试验研究表明,钢筋混凝土结构存在很明显的非线性特性[1-3],这是由于组成钢筋混凝土的材料本身存在非线性.文献[4-5]指出结构的弹性分析不能较好地反映混凝土和钢筋之间的变形协调问题,不能合理的反映在长期荷载作用下混凝土构件的内力和变形,所以按照线弹性理论方法求得的结构内力和变形不能反映实际情况.对桥梁结构的材料非线性研究较多,文献[6-7]研究材料非线性采用了广义逆力(generalized inverse matrix,GIM)分析方法,该方法在解决材料非线性问题时无需像传统的基于位移法的逐步增量法那样逐步求解,但是理论性较强,且在非线性方程组求解过程中稳定性不太好;文献[8-10]基于有限元软件分析法,研究了分层有限单元法、分层壳元法以及材料非线性的平面杆系结构有限元分析方法,这些方法各有特点,同时存在一定的不足之处,由于单元划分复杂,非线性方程组求解过程中不一定收敛,存在稳定性和精确性不够的缺点;文献[11]研究材料非线性时采用实测值的反分析方法,该方法需要极高的模型辨识方法,引入进化的思想,利用遗传算法和遗传规划的全局优化搜索技术,进行材料非线性模型识别的进化方法研究,这种方法理论较复杂,在实际工程中很难应用.
综上所述,很少有文献研究多梁式T梁桥的材料非线性问题,文中采用软件OpenSEES[12-13]的纤维模型分析多梁式钢筋混凝土结构材料非线性,基于OpenSEES这个软件本身存在的优点能够克服非线性方程组求解过程中稳定性和精确性不够的缺点,建立纤维模型可以将构件截面划分,从而同一截面的不同纤维可以有不同的单轴应力应变关系,这样就可以采用更加符合构件受力状态的单轴本构关系,更好的模拟钢筋和混凝土之间的实际工作性能,用OpenSEES计算结果与试验结果数据进行了对比分析,结果相吻合,为多梁式钢筋混凝土桥梁的材料非线性分析提供了一种实用的计算方法.
1纤维模型
纤维模型是OpenSEES程序内部的一种模型,该模型将构件截面划分成很多纤维,对于钢筋混凝土结构,截面就包括钢筋纤维和混凝土纤维,对于每一根纤维考虑它自身的轴向本构关系,不同的纤维就有不同的本构关系.构件的纤维单元划分见图1.

图1 纤维模型划分示意图
纤维模型截面分析前,首先应该对构件的横截面进行划分.混凝土按其位置及所受约束情况进行划分.OpenSEES根据构件截面上的保护层混凝土和受约束区核心混凝土的应力应变关系不同将混凝土纤维区分为OpenSEES中的coverconcrete和coreconcrete,钢筋纤维应该注意使钢筋单元与原截面钢筋的形心相重合,划分见图2.

图2 钢筋混凝土T梁纤维截面图
2本构关系
2.1混凝土本构关系
纤维模型中混凝土受压时的单调加载骨架曲线(见图3)采用Scott等改进后的Kent-Park模型[14].该模型综合考虑到横向箍筋对核心混凝土的约束影响,所以通过用修正参数修正图中混凝土骨架曲线的峰值应力应变和软化段的斜率来实现目标,其中受压骨架曲线表达式如下.
(1)
(2)
式中:K为混凝土强度增加系数,0.002K是对应的峰值应变,
(3)
Zm为混凝土应变软化段斜率,
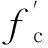
针对混凝土受箍筋加拉筋约束的情形,Scott给出了混凝土极限压应变偏保守的取值方法,按下式计算.
(5)

图3 混凝土单调加载骨架曲线
2.2钢筋本构关系
该模型为考虑等向应变硬化影响的本构关系模型,见图4.

图4 Menegotto-Pinto钢筋模型
该本构关系模型计算上非常有效率是由于采用了应变的显函数表达形式,同时又保持了与钢筋重复加载试验所得的结果具有很好的一致性,可以反映包兴格(bauschinger)效应,模型数学表达式如下.
(6)
式中:
(7)
其中:(ε0,σ0)和(εr,σr)的具体含义见图4;b为应变硬化率;R为影响过渡曲线形状的参数,它反映了包兴格效应,即
(8)
式中:将随每次应变的反向而更新数值;R0为首次加载时R的初始值;a1和a2是同R0由试验确定的参数值.为了解决钢筋等向硬化的问题,Filippou等指出将线性的屈服渐近线进行应力平移,塑性应变最大值的大小决定的平移大小,表达式为
(9)
式中:εmax为应变反向时应变的最大绝对值;σy,εy分别为屈服应力和屈服应变;a3与a4为由试验确定的参数值.
3工程实例
3.1工程概况
以某多梁式T梁桥为背景桥,钢筋混凝土多梁式的上部结构单跨横向布置4片T梁,T梁截面及钢筋布置见图5、图6,该桥跨径为9.2 m.分别在跨中和支座处设置横隔板.该桥使用了40 a后,在1993年废除使用,废除前进行了现场破坏性试验,现场试验对T梁进行混凝土钻心取样,实际测得混凝土的弹性模量Ec=23 530 MPa,混凝土的抗拉强度ft=2.21 MPa,抗压强度fc=23.5 MPa,对钢筋试样进行测试得到钢筋的屈服强度fy=254.8 MPa.

图5 桥梁横断面布置图(单位:mm)
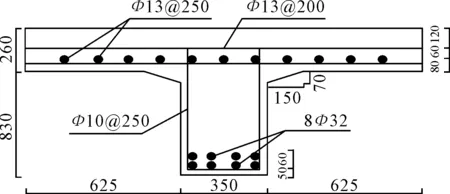
图6 单片T梁截面布置图(单位:mm)
3.2加载方式
采取3种加载方式,即中载、偏载,以及均匀加载,对该桥做了偏载的破坏试验,并做了相关的多梁式梁桥全过程破坏分析,编制组合分层壳单元的非线性有限元程序,对该桥进行了非线性有限元的模拟分析[16-17].
1) 偏载加载方式为了模拟实际的车辆作用,采用4个加载点施加集中荷载,每级施加3t的力,逐级加载直到梁破坏以测试多梁式T梁的极限承载能力,在破坏性试验中,实际加载的配备装备及加载方式见图7、图8,其中G1,G2,G3,G4分别表示第一片至第四片梁.

图7 偏载加载方式(单位:mm)

图8 偏载加载设备
在偏载加载方式下,每片主梁的试验数值与有限元数值的荷载-位移对比曲线见图9,从图中分析可知计算值和试验值比较吻合,说明OpenSEES纤维模型模拟具有较高准确度的特点,由于偏载方式加载,把荷载加到主梁G1和G2的跨中处,使得G1和G2主梁跨中位置成为挠度敏感区,所以其试验数据与OpenSEES有限元数据计算结果相当接近,吻合程度高,而相对于主梁G3和G4而言,不是挠度敏感区,尤其是主梁G4,试验数据本身也不光滑而且存在误差,所以试验数据和OpenSEES有限元计算结果不是太吻合,存在一定的误差.

图9 各片主梁跨中的荷载-挠度曲线(试验数据对比)
图10为各主梁跨中的荷载-挠度.由图10可见,由于偏载方式加载,每片梁进入屈服阶段时的屈服点不同,在相同荷载作用下,主梁G1的跨中挠度最大,刚度折减现象最严重,而主梁G4还几乎处于弹性阶段,没有达到屈服状态,刚度折减现象不太明显.由于是偏载加载方式,当数值模拟的实际加载量在105 t时,G1梁完全破坏,整个结构失效,但是G4梁还仍然存在一定的刚度,还能承受荷载.然而,实际试验测得实际加载量为102 t时,才达到上述状态,说明数值模拟和试验数据误差很小,误差仅是2.9%.

图10 各主梁跨中的荷载-挠度

图11 各梁受拉区纵向钢筋应力随荷载的变化
图11为各梁受拉区纵向钢筋应力随荷载的变化图.由图11可见,由于偏载加载方式,G1主梁的受拉区钢筋应力最大而且应力发展相对最快,荷载加载到24级左右时,即加载量达到72 t时,G1主梁的受拉区纵向钢筋首先开始屈服,进入屈服阶段,之后钢筋进入硬化阶段,应力发展较缓慢.主梁G2的受拉区纵向钢筋加载量达到78 t时,进入屈服阶段,主梁G3的受拉区纵向钢筋加载量达到102 t时,进入屈服阶段,此时,整个结构完全破坏.然而,只有G4主梁的受拉区纵向钢筋还尚未屈服,仍然处于弹性阶段.
2) 中载加载图12为各主梁跨中的位移-荷载等级.由图12可见,由于中载方式加载,荷载施加在主梁G2和G3上,G1主梁和G4主梁荷载-位移曲线相同,G2和G3主梁荷载-位移曲线相同.计算分析说明,荷载加载至25级左右时,即加载量为75 t跨中位移在15 mm时,该结构进入非线性阶段,当继续加大荷载,当34.5级时,即加载量为103.5 t时,跨中位移18 mm左右时,结构发生破坏.从图13分析可知,在中载加载方式下,G1主梁和G4主梁的受拉区纵向钢筋应力变化是相同的,而G2主梁和G3主梁的受拉区纵向钢筋应力变化是相同的,荷载加至28级时,主梁G2和G3的受拉区纵向钢筋开始屈服,继续增加荷载,当荷载增加到34.5级时,主梁G1和G4的受拉区纵向钢筋开始屈服.与偏载加载方式相比较,中载加载时荷载横向分布系数比偏载时较均匀,所以中载加载时钢筋屈服明显的滞后于偏载加载.在偏载加载直到结构破坏时,主梁G4的受拉区钢筋还处于弹性阶段,没有达到屈服状态,而中载作用下,主梁G1和G4的受拉区钢筋在荷载加至34.5级时刚开始屈服.

图12 各主梁跨中的位移-荷载等级

图13 受拉区钢筋应力随加载等级的变化曲线
3) 均匀加载图14为各主梁在均匀加载下跨中位移-荷载曲线.由图14知,由于均匀加载,各主梁的荷载-挠度曲线基本是一样的,即G1,G2,G3和 G4主梁荷载-位移曲线重合在一起.计算分析说明,当荷载加至48 t,跨中位移为16 mm时,结构进入非线性阶段,继续加载至破坏时上部结构各片主梁的跨中位移约为28 mm,此时该桥上部结构的极限承载能力约为54 t.

图14 各主梁在均匀加载下跨中位移-荷载曲线
图15为各梁受拉区钢筋应力随加载等级的变化曲线.由图15可见,在均匀加载方式下,各主梁受拉区纵向钢筋应力基本相同的.当荷载加至16.5级,即实际加载量为49.5 t时,所有梁的梁底受拉区纵向钢筋基本同时达到屈服阶段,从此开始进入非线性阶段,由于钢筋的硬化作用,钢筋应力随加载增加,但增加的相当缓慢,之后随着荷载的继续增加,非线性越来越明显,当加载到54 t时,结构开始破坏.

图15 各梁受拉区钢筋应力随加载等级的变化曲线
纵向比较3种加载方式,偏载加载方式下,主梁G1的受拉区纵向钢筋加至24级时进入屈服阶段,在中载下,荷载加至28时,主梁G2和G3的受拉区纵向钢筋开始屈服,而在匀载下,荷载加至16.5级时,所有梁的受拉区纵向钢筋同时屈服,综上所述,在均匀加载方式下主梁钢筋屈服明显早于偏载方式和中载方式.
4结论
1) OpenSEES有限元软件能够克服非线性方程组求解过程中稳定性和精确性不够的缺点.
2) 在偏载加载方式下,提取了多梁式简支T梁桥破坏性试验数据,并与OpenSEES软件模拟的计算值进行了对比分析,误差是2.9%,具有较高的精度.
3) 从荷载等级与位移关系曲线及钢筋应变随荷载等级的变化曲线可以展现该桥梁非线性发展变化的全过程,从线性阶段到最后的破坏阶段.
4) 在3种加载方式下,从荷载-位移曲线和钢筋应力-荷载曲线中可以得出,桥梁结构均匀加载方式比其他两种方式更容易破坏和主梁受拉区纵向钢筋更早开始屈服.
参 考 文 献
[1]过镇海.混凝土的强度和变形(试验基础和本构关系)[M].北京:清华大学出版社,1997..
[2]王心勇,辛全才,宋娟.钢筋混凝土结构的非线性有限元分析[J].人民黄河,2006,28(8):60-61.
[3]李扬.基于材料非线性的构件计算方法的研究[D].武汉:华中科技大学,2009.
[4]何政,欧进萍.钢筋混凝土结构非线性分析[M].哈尔滨:哈尔滨工业大学出版社,2006.
[5]刘禹.纤维布加固钢筋混凝土抗弯构件的非线性有限元分析[D].西安:西安理工大学,2008.
[6]刘西拉,王开健.材料非线性问题的广义逆力法有限元格式表达[J].岩石力学与工程学报,2004,23(21):3629-3635.
[7]J Z C, L L X. A large increment method for material[J]. Advances in Structural Engineering,1997(1):99-110.
[8]潘家英,张国政.大跨度桥梁极限承载力的几何与材料非线性耦合分析[J].土木工程学报,2000,33(1):5-8.
[9]张剑,叶见曙,陈艳,等.基于分层壳元法多梁式T梁的极限承载力评估[J].公路交通科技,2007,24(5):81-85.
[10]曾永革.考虑材料非线性的平面杆系有限元分析方法[J].湘潭师范学院学报:自然科学版,2009,31(2):98-102.
[11]杨成祥.材料非线性模型的进化识别方法研究[D].哈尔滨:东北大学,2001.
[12]陈学伟,韩小雷,林生逸.基于宏观单元的结构非线性分析方法、算例及工程应用[J].工程力学,2010(A01):59-67.
[13]齐虎,孙景江,林淋.OPENSEES中纤维模型的研究[J].世界地震工程,2007,23(4):48-54.
[14]S M, F M, H S. OpenSees users manual[M]. Berkeley: Univ. of California,2006.
[15]凌炯.面向对象开放程序OpenSees在钢筋混凝土结构非线性分析中的应用与初步开发[D].重庆:重庆大学,2004.
[16]张剑.多梁式混凝土梁桥的极限承载力研究[D].南京:东南大学,2007.
[17]SONG Ha-Won, DY K B. Finite element failure analysis of reinforced concrete T-girderbridges[J]. Engineering Structures,2002,24(2):151-162.
Research on the Material Nonlinear of Reinforced
Concrete Bridge Based on Open SEES Fiber
YANG Guojun1)HAO Xianwu1)DUAN Ruifang2)LI Ziqing1)
(SchoolofHighway,Chang’anUniversity,Xi’an710064,China)1)
(ShaanxiCollegeofCommunicationTechnology,Xi’an710013,China)2)
Abstract:In order to improve the nonlinear accuracy of engineering structure, the fiber model of OpenSEES program is studied. Taking the multi-beam reinforced concrete as an example, fiber model is established to analyze the changing process of material nonlinear with each beam through the partial, middle and uniform load. In the partial load mode, the numerical data of load-midspan displacement and load-steel stress is compared with the destructive test data. The results show the simulation error is very small, and the numerical data is consistent with the test data, which shows that analyzing material nonlinearity with the fiber element of OpenSEES finite program has higher accuracy and superiority.
Key words:bridge engineering; fiber model; material nonlinearity; multi-beam reinforced concrete; constitutive relationship
收稿日期:2015-10-28
doi:10.3963/j.issn.2095-3844.2016.01.017
中图法分类号:U448.217
