沥青路面微观纹理分形插值模型参数计算研究*
2016-03-04雷进宇汪恩军王维锋
雷进宇 汪恩军 王维锋
(武汉理工大学智能交通研究中心1) 武汉 430063) (武汉工程大学交通研究中心2) 武汉 430073)
(江苏省交通规划设计院股份有限公司3) 南京 210005)
沥青路面微观纹理分形插值模型参数计算研究*
雷进宇1)汪恩军2)王维锋3)
(武汉理工大学智能交通研究中心1)武汉430063)(武汉工程大学交通研究中心2)武汉430073)
(江苏省交通规划设计院股份有限公司3)南京210005)
摘要:在基于分形的沥青路面微观纹理特征描述中,如何选取合适的分形插值垂直比例因子是一个无公认选择标准的问题.文中提出一种适用于沥青路面的分形插值模型的改进算法,将遗传算法和序列二次规划方法结合应用于分形插值模型参数的寻优过程,并在自制沥青试样检测平台采集到的沥青路面微观纹理的基础上进行对比试验.结果表明,经组合优化后的分形插值方法在计算沥青路面复杂微观结构和小尺度特征描述等方面更具优势,它不仅克服了遗传算法中全局最优解求解精度低的问题,且使传统最优化方法的最优解的局限性得到了改善,进一步改进了分形插值结果的精度,实现了路面构造深度曲线的最佳拟合.
关键词:微观纹理;分形插值模型;组合优化;垂直比例因子
雷进宇(1989- ):男,博士,主要研究领域为交通安全与数据可视化
*国家自然科学基金项目资助(批准号:51208394)
0引言
路面的抗滑性能是影响路面行车安全的一个重要因素,且抗滑性能主要受路面纹理的影响,因此如何选择合理的参数来表征路面纹理从而用以研究路面抗滑性能是当下的一个热点.
目前,常用于描述路面纹理特征的传统参数分为两类:垂直方向路面纹理深度参数和水平方向路面纹理波长参数[1].然而传统参数仅从垂直方向、水平方向刻画路面纹理整体的几何形貌,无法全面表征路面纹理.近年来,出现了第三类描述路面纹理特征的新型参数——分形维数[2].由于该参数能综合的描述路面纹理整体自相似的复杂的结构特征,因此分形维数在沥青路面纹理的表征上得到了快速发展.在通过分形插值模型获取分形维数的分析过程中,垂直比例因子的选取在很大程度上决定了最终计算得到的分形维数与实际值的误差.然而目前对如何合理选择该参数达到计算分形维数精度最优的方法没有一个确切选择标准.文献[3]基于遗传理论对路面纹理的分形插值模型的垂直比例因子进行求取,并验证了该方法求得的分维值与路面纹理之间的联系.文献[4]对垂直比例因子进行遗传优化,并将所得结果与ARGO海温资料进行对比表明,优化后的结果在复杂结构和小尺度特征描述方面更具优势.文献[5]利用了粒子群优化算法对垂直比例因子进行寻优,从而求取分形插值的逆问题最优解并通过Weierstrass函数验证了该方法具有较好的插值拟合效果.然而上述这些方法都存在着求解精度不足的缺点,因为其求解精度受限于遗传算法和粒子群算法的随机搜索特性,因此较难得到垂直比例因子的精确最优解.文献[6]提出一种基于遗传算法和序列二次规划算法的混合优化算法,并将其应用于机械臂最优运动规划问题中,并得到较好的优化结果.
文中尝试利用遗传算法和序列二次规划算法相结合的组合优化算法来求解垂直比例因子最优化问题.利用自制的路面纹理检测平台采集沥青试块表面纹理.在采集数据的基础上,采用遗传算法获得垂直比例因子全局最优解的近似值,并以该组近似值为初始点,采用序列二次规划方法搜索出精确的全局最优值.将求解的分形插值模型与采集的路面真实纹理进行比较验证了基于该方法建立的沥青路面分形插值模型优于单纯的遗传算法.
1沥青路面微观纹理分形插值模型
分形插值模型实质上是一种迭代函数系统(IFS),这使其与以多项式或三角函数等初等函数为基函数的传统数学插值或拟合函数存在根本上的不同.它利用迭代系统中的仿射变换对已知数据点进行迭代计算,从而得出一个分形曲线,即该IFS的吸引子[7].它能较好的展现出大自然中物体精细的自相似结构和波动性.因此分形插值函数在路面纹理曲线的拟合和对深入理解路面整体自相似性与复杂性的分形特征上具有独到的优势[8].
定义一组测得的纹理高程数据集合为{(xi,yi)∈R2,i=0,1,…,N}.其中:xi和yi分别为实验测得的沥青路面水平位置和沥青路面距离基准面的高程值.与该数据集相对应的迭代函数系统为{R2;Wn,n=1,2,…,N}.其中:Wn为仿射变换并具有如下构造.
(1)
且Wn需满足式(2)和(3)
(2)
(3)
式(2)和(3)可演变为
(4)

(5)
因此,由上面的分析中可以得出垂直比例因子组dn,它是一个重要的参数,直接决定了迭代函数系统的仿射变换.因此dn取值的细微变动就会引起分形插值函数生成的拟合曲线产生巨大差异.并且dn与被测物体的分形维数有着直接的联系,如果
(6)
且插值点不共线,则伴随与这组数据的分形插值函数形成的曲线的分维数是满足方程
(7)
的惟一实数解D.
2形插值模型垂直比例因子的计算
由上述分形插值原理可知,垂直比例因子的选取将直接影响到插值结果的优劣和最终得到的分维数的准确性.因此如何选择合理的方法来求取适用于沥青路面纹理的垂直比例因子,对建立与沥青路面纹理达到最佳逼近的分形拟合曲线起着十分关键的作用.
遗传算法是一种以自然选择和遗传理论为基础的高效全局寻优搜索算法.它将需优化的参数不断进行选择杂交变异等模拟自然生物进化过程的操作,然后再对其进行优胜劣汰的选择从而经过一代代的淘汰选择出最优的参数,它在全局搜索上存在着巨大的优势的同时也存在求解精度低等不足.序列二次规划方法利用给定的初始值将原问题转换为一系列二次规划问题,在每一次迭代中通过求解二次规划子问题来求取最优解,虽然该方法其求解精度较高,但由于该算法对初始值的敏感性,因此容易陷入局部性的极值而无法计算出全局的最优值.所以,由两者算法相结合的组合优化算法,既能满足求解精度高的要求也达到求解出全局最优解的目的.
文中利用自制的沥青试块实验系统对沥青样块表面100mm长度的断面高程深度值进行连续采集,并每隔5mm取出一高程数据构成一组由21个元素组成的数据集合,从而对应于该数据集的垂直比例因子组为dn,n=1,2,3,…,20.选取这20个因子作为遗传算法的寻优参数,适应值函数为
(8)
式中:f(x)为实验系统测得的沥青路面高程深度值;g(x)为利用分形插值模型计算得到的分形插值函数;N为插值点的个数.
最终经过遗传算法优化得到的dn作为初始值带入序列二次规划方法中进行组合优化,具体流程见图1.

图1 垂直比例因子组合优化流程图
3路面微观纹理分形特征算例
3.1路面微观纹理实验数据采集
3.1.1数据采集系统
见图2和3,系统采用的激光传感器为LMI公司生产的Optocator-2008-128/390F,其分辨率为0.032 mm,采样频率为78 kHz,精确到微米级的采集精度和千赫兹级的采样频率保证了沥青路面试块断面高程信息采集的连续性与准确性.控制芯片采用的是Stm32f417芯片,其工作频率最高可达168 MHz,这为数据的实时采集和传输提供了有利的保障.在数据传输方面,本系统使用以太网和DMA技术相结合的传输方式,并采用LWIP,UDP传输协议和双缓冲数据传输技术,在系统消耗内存最小的情况下实现了数据的实时稳定传输,在试验中经Commview,Wireshark等网络封包分析软件验证该系统在数据传输中没有数据丢包等异常现象存在.最后在上位机中对接收数据采用了数据校验的接收方式进一步确保了数据的准确接收,并以TXT的格式保存以便于后续的数据分析.
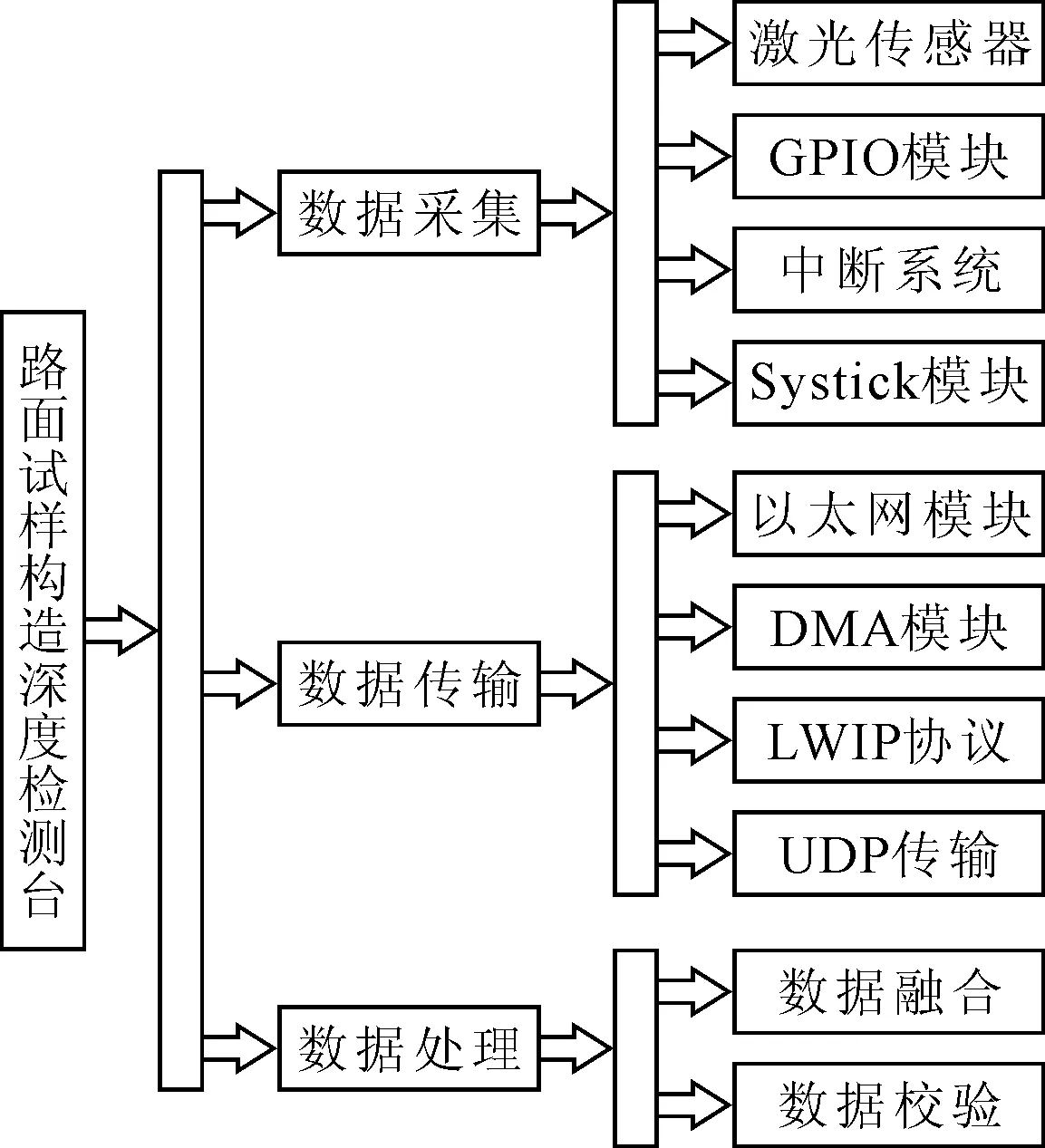
图2 系统功能模块

图3 实验平台照片
3.1.2路面微观纹理数据处理
由于路面缺陷和电磁干扰等原因,接收数据中存在少数异常值,其比例不大于0.8%.这些异常值通常表现为陡升或者陡降,在数据处理中利用设定阈值和3σ准则[10]的方法对其进行过滤得到数据见图4.在处理由激光器摆放方位与实验平台上的沥青试块表面存在一定的角度差而造成的误差时,本文依据ASTM规范[11]中的斜率抑制法进行消除.首先依据采集的断面高程数据计算出其一元线性回归模型见图5,其次,将求出的回归线视为基准路面纹理的平均深度值,利用采集到的数据减去平均深度值从而得到了最终准确的断面高程数据,见图6斜率抑制法有效的减少了角度差对数据造成的误差.

图4 异常值修正后

图5 一元线性回归模型

图6 斜率抑制修正后
3.2路面微观纹理实验数据分析
3.2.12种不同寻优方法得到的适应度的比较
在优化过程中,适应度即适应值函数的值,是能最直观的反映出得到的优化参数优劣的评价指标之一.因此,在文中适应度越小表示分形插值数据与原始路面纹理之间的误差就越小,即计算得到的垂直比例因子参数就越接近最优解.实验中,对4种样块中的每一种沥青样块表面皆采集10条100 mm的纹理并利用遗传算法和组合优化算法进行分形插值,并列出了2种不同寻优方法得到的适应度的比较,见表1(表中ga为遗传算法,gs为组合优化算法).
由表1中可以看出,在4种不同沥青样本的实验中,利用组合优化算法得到的适应度皆小于遗传算法得到的适应度,这表明了利用组合优化算法得出的垂直比例因子组优于单纯的遗传算法所求得的解.

表1 适应度比较
3.2.2分形插值曲线的逼近度比较
依据2种不同寻优方法计算得出的垂直比例因子组所生成的分形插值曲线与路面真实纹理的逼近程度也是用于判别垂直比例因子组优劣的主要指标.文中分别列出4种不同类型的沥青试块的分形插值曲线图,见图7~图10.
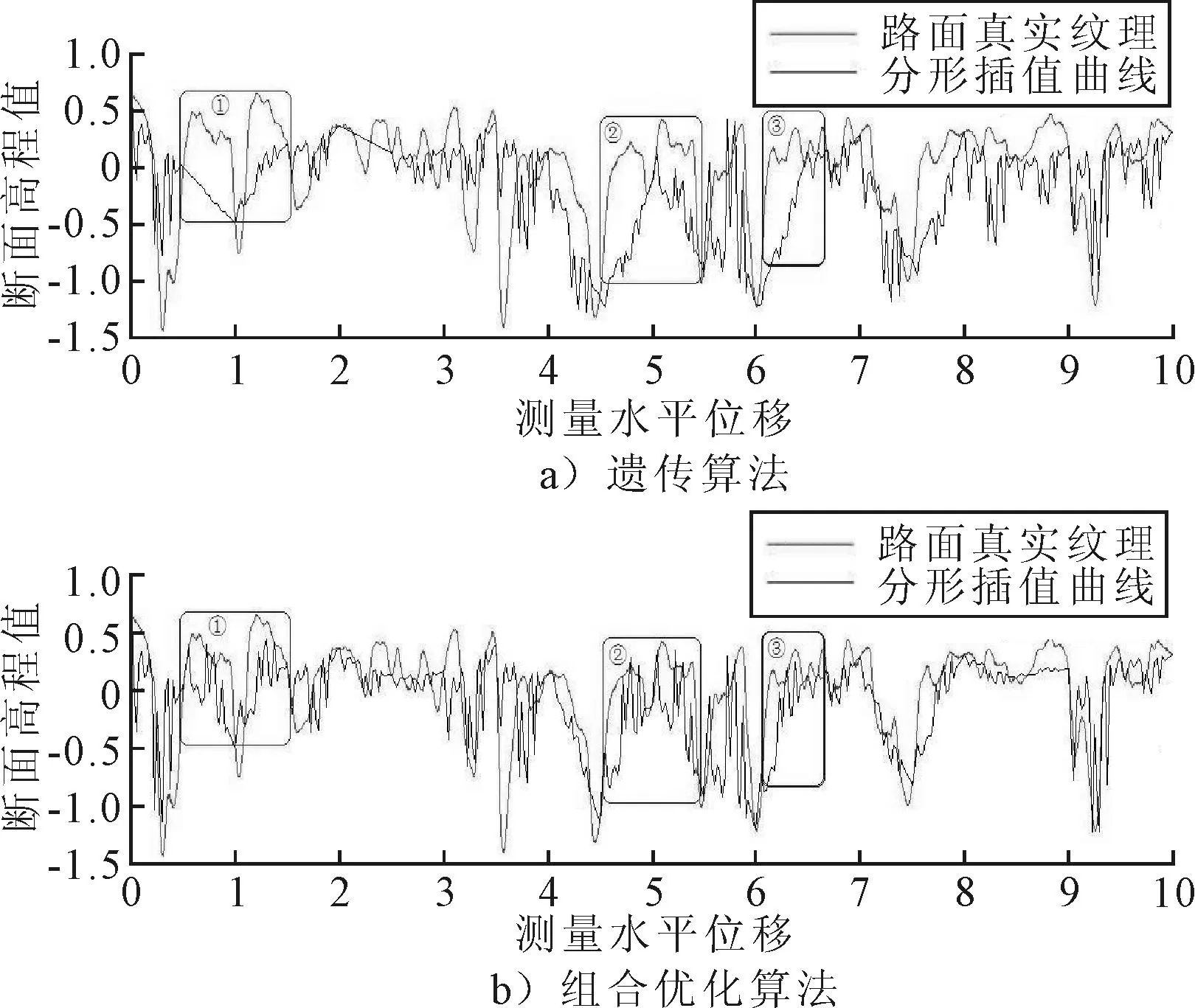
图7 AC13的分形插值曲线图
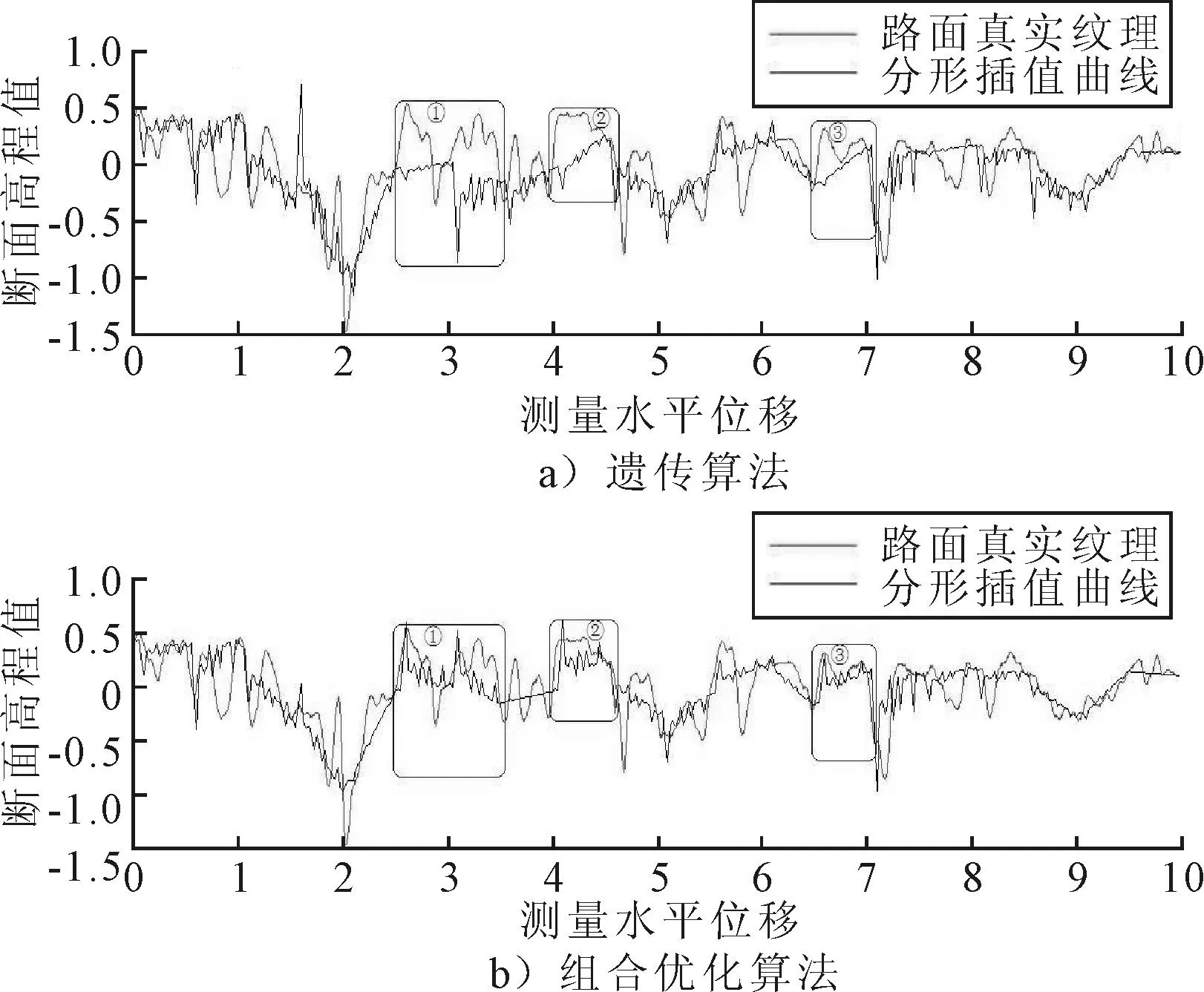
图8 SHRP12.5的分形插值曲线图

图9 SMA13的分形插值曲线图

图10 OGFC13的分形插值曲线图
由图中所标示出的①②③方框可看出,由组合优化方法算出的分形曲线与路面真实纹理更为逼近,且表现出来的曲线的复杂微观结构更为丰富,因此该方法在路面纹理小尺度特征描述方面更具优势.
3.2.3相对误差限比较
Fraclab是一款由法国国家信息与自动化研究所(INRIA)研发的Matlab工具箱.该工具箱被广泛应用在地球物理学、信号与图像处理、经济学等利用到分形分析的学科中.为了验证2种方法算出的分维数的准确性,文中利用Matlab中的工具箱Fraclab计算出的分维值作为参照比较,并按照式(9)算出他们的相对误差限,见图11.由图11可见,利用组合优化算法所得到的分维值的相对误差限均低于10%,且在4种样本中该算法的精确性均优于遗传算法.
(9)
式中:f为利用算法求得的分维数;ffl为工具箱所求出的分维值.
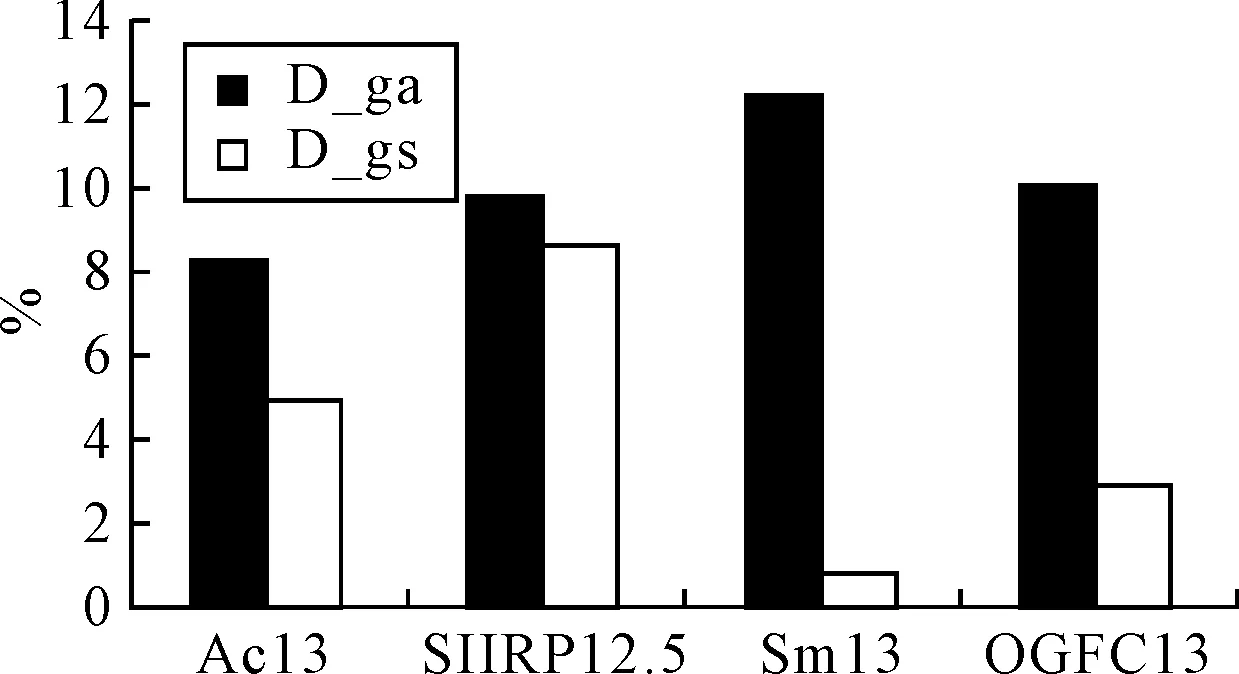
图11 相对误差限比较
4结论
1) 利用组合优化算法得到的适应度皆小于遗传算法得到的适应度,因此利用组合优化算法所求得的解更优.
2) 由组合优化方法算出的分形曲线与路面真实纹理更为逼近,且表现出来的曲线的微观结构更为丰富,因此该方法在描述路面纹理复杂自相似等分形特征更具优势.
3) 利用组合优化算法所得到的分维值的相对误差限均低于遗传算法,该算法得到分维的精确性均优于遗传算法.
目前,受实验条件的制约,尚无法全面的展示试块的表面微观纹理.在后续的研究中拟采用图像处理技术,对沥青试块进行三维重建,从而得到沥青试块表面丰富的纹理高程数据,从而利用组合优化算法对不同的沥青试块的分形插值模型进行更细致的分析.
参 考 文 献
[1]初秀民,李永,严新平.基于微观形貌特征的沥青路面抗滑性能评价研究进展[J].交通与计算机,2007,25(1):24-26.
[2]KOKKALIS A G, TSOHOS G H, PANAGOULI O K. Consideration of fractals potential in pavement skid resistance evaluation[J].Journal of Transportation Engineering,2002,128(6):591-595.
[3]王维锋,严新平,初秀民.基于分形理论的沥青路面微观形貌特征描述与求解方法[J].吉林大学学报:工学版,2010,40(6):1538-1542.
[4]刘巍,张韧,王辉赞.分形插值参数的遗传优化及其ARGO海温场应用试验[J].大气科学学报,2010,33(2):186-192.
[5]袁利国,聂笃宪,旷菊红.粒子群优化算法解分形插值的逆问题[J].计算机与数字工程,2007,35(9):44-45.
[6]连广宇,孙增圻.机械臂最优运动规划问题的混合求解[J].控制与决策,2004,S19(1):102-104.
[7]孙霞,吴自勤,黄畇.分形原理及其应用[M].合肥:中国科学技术大学出版社,2003.
[8]李智,刘涛.基于分形理论评价沥青路面微观构造[J].武汉理工大学学报报:交通科学与工程版,2013,37(3):501-504.
[9]李水根.分形[M].北京:高等教育出版社,2004.
[10]WANG Enjun, WU Jianbo, YANG Xiaohui, et al. Vibration monitoring system of transportation on road based on CAN[C]. Proceedings of the 2nd International Conference on Transportation Information and Safety,2013:1679-1685.
[11]ASTM. Road and paving materials; vehicle-pavement systems[S]. Annual Book of ASTM Standards, E965-06, West Conshohocken, Pa,2006.
Research on Calculation of Fractal Interpolation
Model Parameter of Asphalt Micro-texture
LEI Jinyu1)WANG Enjun2)WANG Weifeng3)
(IntelligentTransportationSystemsResearchCenter,
WuhanUniversityofTechnology,Wuhan430063,China)1)
(TransportationResearchCenter,WuhanInstituteofTechnology,Wuhan430073,China)2)
(JiangsuProvinceCommunicationsPlanningandDesign
InstituteCompany,Nanjing210005,China)3)
Abstract:Since there is no accurate method to calculate the fractal interpolation model of micro-texture on asphalt pavement, a hybrid optimization algorithm combined genetic algorithm (GA) and sequential quadratic programming (SQP) is put forward in the research of vertical scaling factors in the fractal interpolation model. Additional, a high-precision laser range finder, which is constituted by laser sensor and chip STM32F417, was designed to measure the asphalt pavement texture for comparison. The comparison experiment showed that the fractal interpolation model calculated by hybrid optimization algorithm is better than the model optimized by GA in terms of fitness, approximation degree of interpolation curve and the accuracy of fractal dimension.
Key words:micro-texture; fractal interpolation model; hybrid optimization; vertical scaling factors
收稿日期:2015-11-10
doi:10.3963/j.issn.2095-3844.2016.01.006
中图法分类号:U416.217
